Σκέψεις, διευκρινίσεις και περίεργα για τη Φυσική.
Αφιερωμένο στους καθηγητές μου, Άννα Κυριακίδου και Νίκο Πασχαλούδη.
Πηγή εικόνων: public domain
Σχετικά είναι και τα θέματα του κουίζ στο ίδιο blog: https://geometax12.blogspot.com/2018/07/blog-55.htm
Να γιατί οι δάσκαλοι της Φυσικής δεν πρέπει να απασχολούνται με τους μαθητές στο διάλειμμα.
105. Πόση ισχύ έχει ένα επιβατικό αεροπλάνο;
Να γιατί οι δάσκαλοι της Φυσικής δεν πρέπει να απασχολούνται με τους μαθητές στο διάλειμμα.
0. Τι είναι επιστήμη.
1. Μέτρον άριστον.
2. Μάζα – Βάρος.
3. Μεταβολή του βάρους στη Γη.
4. Πτώση και βαρύτητα.
5. Γιατί ο Αριστοτέλης είχε άδικο.
6. Δράση – Αντίδραση.
7. Διελκυστίνδα και συγκρούσεις.
8. Είναι σταθερές η Στατική Τριβή και η Αντίδραση;
9. «Φυγόκεντρος» δύναμη.
10. Η πίεση δεν εφαρμόζεται!
11. Ορμή και Κινητική Ενέργεια.
12α. Ροπή και Ισχύς.
12β. Πόσους ίππους έχει ένα άλογο;
13. Άνωση, ή Άντωση;
14. Που οφείλεται η Άντωση σε πτέρυγα;
15. Ποδήλατα, νεροχύτες και γυροσκοπικά φαινόμενα.
16. Έλικες και αεριοστρόβιλοι.
17. Άνωση και βαρύτητα.
18. Η ταχύτητα του ηλεκτρικού ρεύματος.
19α. Πρόσθεση παράλληλων αντιστάσεων.
19β. Γιατί οι τύποι πρόσθεσης πυκνωτών είναι αντίστροφοι από των αντιστάσεων; Και κάτι ακόμα.
20. Πότε καίγονται οι λάμπες.
21. Τάση και Ένταση του ηλεκτρικού ρεύματος. Ποιά είναι πιο επικίνδυνη;
22. Ενεργή (πραγματική) και Άεργος Ισχύς και Ενέργεια.
23. Mια αντίσταση διαφορετική από τις άλλες.
24. Τα όρια της Ατμόσφαιρας, του Διαστήματος και της Βαρύτητας.
25. Ποια είναι η θερμοκρασία του Διαστήματος;
26. Ποια είναι η πρωταρχική πηγή των ανανεώσιμων πηγών ενέργειας;
27. Το σφαιρικό σχήμα.
28. Γιατί δεν έχει νόημα το Αεικίνητο.
29. Καλή ταλάντωση εναντίον κακής ταλάντωσης.
30. Μικροσκόπια και τηλεσκόπια.
31. Η φωνή του «Ντόναλτ Ντακ».
32. Το παράδοξο με την ταχύτητα του φωτός.
33. Θα μπορέσουμε ποτέ να ξεπεράσουμε την ταχύτητα του φωτός;
34. Οδηγίες για μελλοντικούς ... Jedi.
35. Αύξηση της «μάζας» κοντά στην ταχύτητα του φωτός.
36. Επίδραση της ταχύτητας και της μάζας στον χρόνο.
37. Η θεωρία της Σχετικότητας, δύο θεωρίες σε μία.
38. Τελικά τι είναι το φωτόνιο? Και η ταχύτητα του φωτός.
39. Γιατί είναι δύσκολο να κατανοήσουμε την Κβαντομηχανική;
40. Η πυρηνική ενέργεια. Τόσο απλή, τόσο πολύπλοκη!
41. Ώσμωση, ένα περίεργο φαινόμενο.
42. Βράσιμο χωρίς, και άναμμα φωτιάς με, ... αέρα.
43. Τριβή και λάστιχα αυτοκινήτων.
44. Η πίεση των υγρών.
43. Τριβή και λάστιχα αυτοκινήτων.
44. Η πίεση των υγρών.
45. Γιατί όλες οι παλίρροιες δεν είναι ίσες.
46. Ένα σιφόνι από μπίλιες.
47. Η επίπεδη τροχαλία που δεν είναι ... επίπεδη.
48. Το «γαλόνι» της Σιτροέν.
49. Άξονες και ροπή, καλώδια και ένταση.
50. Πώς θα καλύψουμε τις μεγάλες αποστάσεις στο Διάστημα.
51. Το "αλλόκοτο" φαινόμενο Mpemba.
51. Το "αλλόκοτο" φαινόμενο Mpemba.
52. Πετάει ο βάτραχος;
53. Η Φύση αγαπάει την "αταξία"!
53. Η Φύση αγαπάει την "αταξία"!
54. H Θάτσερ και το μποζόνιο του Higgs.
55. Ζάρια ή ταχυδακτυλουργικά?
56. Μη Νευτώνια ρευστά.
57. Σπηλαίωση. Πρόβλημα ή λύση;
60. Το νερό, ένα "μαγικό" υγρό.
61. Βαθμός απόδοσης 300%?
55. Ζάρια ή ταχυδακτυλουργικά?
56. Μη Νευτώνια ρευστά.
57. Σπηλαίωση. Πρόβλημα ή λύση;
58. Γιατί τα κύματα είναι χρήσιμα;
59. Τρείς απίθανες θέσεις της σύγχρονης Φυσικής.60. Το νερό, ένα "μαγικό" υγρό.
61. Βαθμός απόδοσης 300%?
62. Γιατί τα μεταλλικά αντικείμενα είναι κρύα στην αφή;
63. Δυνάμεις διαστολής.
64. Ιστιοφόρο ταχύτερο από τον άνεμο;65. 2000 βαθμοί Κελσίου, και όμως παγωνιά!
66. Χαμηλές και υψηλές συχνότητες.
67. Ταχύτητα τροχιάς και ταχύτητα διαφυγής.
68. Οι καμινάδες που πέφτουν και οι μαύρες τρύπες.
69. Όταν δύο γάστρες πλοίου έχουν μικρότερη αντίσταση από μία.
70. Όταν οι πολλοί στρόβιλοι είναι καλύτεροι από τον έναν.
71. Πόσο μεγάλο είναι το Σύμπαν;
72. Ψυχρή συγκόλληση μετάλλων στο Διάστημα.
83. Τα θανάσιμα όμοια τρίγωνα.
84. Stealth (απόκρυψη) εναντίον αεροδυναμικής.
85. Η γοητεία των Νεπέριων λογαρίθμων
86. Οι παρεξηγημένοι σπινθήρες.
87. Προσδιορίζοντας την Απροσδιοριστία.
88. Ισχύει ο νόμος του Μέρφυ; Και το φαινόμενο του "μαύρου κύκνου"
89. Ο "παλμός" της Γης.
90. Η σιωπηλή πτήση της Τυτώς.
66. Χαμηλές και υψηλές συχνότητες.
67. Ταχύτητα τροχιάς και ταχύτητα διαφυγής.
68. Οι καμινάδες που πέφτουν και οι μαύρες τρύπες.
69. Όταν δύο γάστρες πλοίου έχουν μικρότερη αντίσταση από μία.
70. Όταν οι πολλοί στρόβιλοι είναι καλύτεροι από τον έναν.
71. Πόσο μεγάλο είναι το Σύμπαν;
72. Ψυχρή συγκόλληση μετάλλων στο Διάστημα.
73. Πηγή τάσης και πηγή ρεύματος.
74. Το μαύρο ταιριάζει στα ψυγεία.
75. Η στροφορμή του πατινέρ.
76. Η χαμένη τέχνη του λογαριθμικού κανόνα.
77. Η Γη αδυνατίζει!
78. Ένας «μαγικός» συγχρονισμός.
79. Το ψυγείο που «εξαφανίστηκε».
80. Πώς ο άνθρωπος θα μπορούσε να αντέξει απεριόριστα g.
81. Tα φωτόσπαθα των Jedi και η ατμοσφαιρική ρύπανση.
82. Η "μαγική" πτήση του άλμπατρος.
74. Το μαύρο ταιριάζει στα ψυγεία.
75. Η στροφορμή του πατινέρ.
76. Η χαμένη τέχνη του λογαριθμικού κανόνα.
77. Η Γη αδυνατίζει!
78. Ένας «μαγικός» συγχρονισμός.
79. Το ψυγείο που «εξαφανίστηκε».
80. Πώς ο άνθρωπος θα μπορούσε να αντέξει απεριόριστα g.
81. Tα φωτόσπαθα των Jedi και η ατμοσφαιρική ρύπανση.
82. Η "μαγική" πτήση του άλμπατρος.
84. Stealth (απόκρυψη) εναντίον αεροδυναμικής.
85. Η γοητεία των Νεπέριων λογαρίθμων
86. Οι παρεξηγημένοι σπινθήρες.
87. Προσδιορίζοντας την Απροσδιοριστία.
88. Ισχύει ο νόμος του Μέρφυ; Και το φαινόμενο του "μαύρου κύκνου"
89. Ο "παλμός" της Γης.
90. Η σιωπηλή πτήση της Τυτώς.
91. Μια καμπίνα "φυσαρμόνικα".
92. Πού πραγματικά οφείλεται η άνωση;
93. Πόσο κρύο είναι το κενό;
94. Μια απίθανη αντανάκλαση.
95. «Κώνος του Mach» για το φως;
96. Μια "φτηνή" βόλτα στο Διάστημα.
97. Γιατί απωθούνται τα ομώνυμα και έλκονται τα ετερώνυμα φορτία;
98. Δύο τύποι τόσο όμοιοι και τόσο διαφορετικοί.
99. Η πολύπλοκη Φυσική των ελεύθερων σκοπευτών.
100. Γιατί το γυαλί είναι διάφανο;
101. Τέσσερεις διαφορετικές συσκευές για το ίδιο φυσικό μέγεθος.
102. Ψάρια ζόμπι!
103. Γιατί συμβαίνει η Διάθλαση;
104. Μετασχηματιστές και κιβώτια ταχυτήτων.105. Πόση ισχύ έχει ένα επιβατικό αεροπλάνο;
106. Οι καμπύλες ακτίνες τροχών και τροχαλιών.
107. Ηλεκτρολυτική διάβρωση, μια ανεπιθύμητη μπαταρία.
108. Θερμοκρασία και άνεση.
109. Πώς να σας γυρίσει...μπούμερανγκ.
110. Σελήνη τα... "μέσα - έξω"
111. "Φαντάσματα" της Επιστήμης.
112. Σύντηξη και Σχάση.
113. Γιατί οι γεννήτριες των αεροπλάνων παράγουν 400Hz;
114. Πώς δημιουργείται η ηλεκτρομαγνητική επαγωγή;
115. Τι είναι το κυκλικό μεταλλικό δικτύωμα γύρω από τη θέση της μεγάλης δεξαμενής, στο Γκάζι;
116. Το αναγεννητικό φρενάρισμα των ηλεκτρικών αυτοκινήτων.
117. Και λίγα για τους κινητήρες των ηλεκτρικών αυτοκινήτων.
118. Τρία διαφορετικά...διαφορικά (Variomatic, Torsen και Επικυκλικό).
119. Το παράδοξο με τον συντελεστής θερμικής διαστολής όγκου.
120. Ένας "μύθος" για τους ηλεκτροκινητήρες συνεχούς ρεύματος.
121. kilo ή Kilo;
122. Η μοτοσυκλέτα που τρέμει (wobble).
123. Μία περίεργη καμπύλη (καμπύλη του Paschen).
124. Μια ατίθαση πεταλούδα (φαινόμενο Dzhanibekov).
125. Ένα ιδιαίτερο ελατήριο.
126. Ένα "ψυγείο" στην έρημο, 2400 ετών.
127. Το "υγρό" με το μεγαλύτερο ιξώδες.
0. Τι είναι επιστήμη.
Επιστήμη είναι ο συσχετισμός αιτίας και αποτελέσματος διαφόρων φυσικών φαινομένων, με μια διαδικασία που βασίζεται στην παρατήρηση, υποστηρίζεται από τη θεωρία, και επιβεβαιώνεται με το πείραμα.
Η παρατήρηση πρέπει να περιλαμβάνει ποσοτικά (μετρήσιμα) και όχι απλά ποιοτικά μεγέθη, και οι μετρήσεις θα πρέπει να καταλήγουν πάντα στα ίδια αποτελέσματα, όταν οι συνθήκες είναι ακριβώς οι ίδιες.
Υπάρχει βέβαια περίπτωση να μην υπάρχουν πειραματικά δεδομένα, ούτε καν μετρήσιμα μεγέθη, αλλά τότε τα αποτελέσματα θα πρέπει να συνάγονται με μαθηματικό ή λογικό (που είναι περίπου το ίδιο) τρόπο, ξεκινώντας από ήδη αποδεδειγμένες παραδοχές και χρησιμοποιώντας μαθηματικές σχέσεις, που η ισχύς τους έχει ήδη αποδειχτεί ... επιστημονικά.
Η παρατήρηση πρέπει να περιλαμβάνει ποσοτικά (μετρήσιμα) και όχι απλά ποιοτικά μεγέθη, και οι μετρήσεις θα πρέπει να καταλήγουν πάντα στα ίδια αποτελέσματα, όταν οι συνθήκες είναι ακριβώς οι ίδιες.
Υπάρχει βέβαια περίπτωση να μην υπάρχουν πειραματικά δεδομένα, ούτε καν μετρήσιμα μεγέθη, αλλά τότε τα αποτελέσματα θα πρέπει να συνάγονται με μαθηματικό ή λογικό (που είναι περίπου το ίδιο) τρόπο, ξεκινώντας από ήδη αποδεδειγμένες παραδοχές και χρησιμοποιώντας μαθηματικές σχέσεις, που η ισχύς τους έχει ήδη αποδειχτεί ... επιστημονικά.
Τρείς από τους "γίγαντες της Επιστήμης".
Χαρακτηριστικό παράδειγμα, η πρόσφατη (Φεβρ. 2016) επιβεβαίωση (μέσω παρατήρησης και μετρήσεων) της ύπαρξης βαρυτικών κυμάτων, κάτι στο οποίο είχε καταλήξει ο Αϊνστάιν 100 χρόνια νωρίτερα, χρησιμοποιώντας μόνο μολύβι και χαρτί!
1. Μέτρον άριστον (και όχι: "παν" μέτρον άριστον).
Το μέτρο (σαν στάση ζωής), πέρα από τα πλεονεκτήματα που προσφέρει στη ζωή των ανθρώπων, είναι απαραίτητο (σαν σύστημα μετρήσεων) και για την ανάπτυξη του πολιτισμού τους.
Η μέτρηση είναι στην πραγματικότητα η σύγκριση διαφόρων φυσικών μεγεθών με κάποιο κοινά αποδεκτό πρότυπο, ώστε να μπορούμε να μιλάμε την «ίδια τεχνική γλώσσα» από απόσταση.
Με την εξέλιξη της τεχνολογίας οι απαιτήσεις ακρίβειας των μετρήσεων αυξήθηκαν, και για παράδειγμα οι τελευταίες εξελίξεις στο χώρο του Διαστήματος ως προς τη μέτρηση αποστάσεων, προϋπόθεταν τη δυνατότητα μέτρησης του χρόνου με πολύ μεγάλη ακρίβεια (βλέπε επίσης θέμα Νο 36).
Καθώς στην πραγματικότητα δεν υπάρχει απόλυτη ακριβής μέτρηση, αυτό που έχει σημασία είναι:
-Να είναι η ακρίβεια (ή τα περιθώρια σφάλματος) της μέτρησης γνωστά.
-Αυτά τα περιθώρια σφάλματος, να είναι αποδεκτά για το σκοπό της μέτρησης.
Ο επίσημος έλεγχος της ακρίβειας ενός οργάνου ονομάζεται "διακρίβωση" και είναι τμήμα μιας διαδικασίας τεσσάρων επιπέδων, με το καθένα να προσφέρει ακρίβεια καλύτερη κατά μια ή και δύο τάξεις μεγέθους από την επόμενη (προς τα κάτω):
-Εθνικά πρότυπα,
-Εργαστηριακά πρότυπα ειδικά διαπιστευμένων εταιρειών,
-Πρότυπα εταιρειών - πελατών,
-Φορητά όργανα των εταιρειών - πελατών, που χρησιμοποιούνται στο πεδίο.
Σήμερα πλέον μιλάμε για "αβεβαιότητα" μιας μέτρησης, έναν όρο που περιλαμβάνει τόσο το σφάλμα του οργάνου όσο και την επαναληψιμότητα της μέτρησης.
Το σφάλμα του οργάνου, εφόσον είναι συστηματικό, μπορεί να ληφθεί υπόψην και να διορθωθεί, είτε με ρύθμιση, είτε με υποσημείωση που θα συνοδεύει το όργανο.
Η κακή επαναληψιμότητα, μπορεί να οφείλεται είτε στο όργανο (φθορά), είτε στον χρήστη (απροσεξία, κακή όραση, ασταθές χέρι), είτε στις τοπικές συνθήκες (θερμοκρασία, άνεμος, κραδασμοί, υψόμετρο κλπ). Είναι όμως σαφώς πιο δύσκολο να διορθωθεί, ειδικά αν οφείλεται στους δύο πρώτους παράγοντες.
Στην εικόνα κάτω, όπου χρησιμοποιείται το παράδειγμα της σκοποβολής, η ακρίβεια είναι το αντίστροφο του σφάλματος, ενώ η "αξιοπιστία" έχει την έννοια της επαναληψιμότητας, με τη δεύτερη πάντως να είναι σωστότερος όρος.
2. Μάζα – Βάρος.
Συχνά υπάρχει σύγχυση μεταξύ των εννοιών μάζας και βάρους.
Ένας βασικός λόγος είναι ότι στην καθημερινότητα χρησιμοποιούμε τη μονάδα μάζας για να δηλώσουμε ουσιαστικά το βάρος.
Όπως είναι γνωστό, η μάζα είναι η ποσότητα της ύλης που περιέχει ένα σώμα, μετριέται σε κιλά (kg) και είναι ανεξάρτητη από το βαρυτικό πεδίο.
Αντίθετα, το βάρος ενός σώματος είναι η δύναμη που ασκείται επάνω του όταν βρίσκεται μέσα σ’ ένα βαρυτικό πεδίο, και μετριέται σε Νιούτον (Ν).
Και μάλιστα, το βάρος γίνεται αντιληπτό (και μπορεί να μετρηθεί), μόνον εφόσον η δύναμη της βαρύτητας δεν επιταχύνει ένα σώμα, όπως για παράδειγμα όταν το σώμα (και η ζυγαριά) είναι ακίνητα, αλλά και όταν να κινούνται με σταθερή ταχύτητα, όπως μέσα σ’ένα όχημα ή ασανσέρ.
Αντίθετα, στον Διαστημικό Σταθμό τα σώματα δεν έχουν βάρους, παρότι ο διαστημικός σταθμός κινείται με σταθερή γραμμική ταχύτητα, επειδή υπάρχει συνεχώς η κεντρομόλος επιτάχυνση της Γης που τον κρατάει σε τροχιά, έτσι ώστε πρακτικά να μην υπάρχει βαρυτικό πεδίο μέσα στον σταθμό (σήμερα λέμε ότι υπάρχει «μικροβαρύτητα» τόσο μέσα στον Διαστημικό Σταθμό, όσο και στο Διάστημα).
Στη Γη λοιπόν, μια και οι διαφορές βαρύτητας είναι μικρές στην επιφάνειά της, χρησιμοποιούμε το βάρος (που είναι ευκολότερο να μετρηθεί) για να «ζυγίσουμε» κάτι, ενώ χρησιμοποιούμε καταχρηστικά τη μονάδα μάζας (δηλαδή το κιλό) για να υποδηλώσουμε στην ουσία το βάρος, το οποίο θα έπρεπε να μετριέται κανονικά σε Νιούτον.
Παλαιότερα μάλιστα, για να «βολευτεί» αυτή η ασυνέπεια, χρησιμοποιούσαμε για το βάρος το «κιλό βάρους» ή κιλοπόντ (kp), που αντιστοιχούσε σε μάζα ενός κιλού στην επιφάνεια της Γης.
Σήμερα λοιπόν, όταν πάμε να αγοράσουμε «ένα κιλό» ζάχαρη, εννοούμε ουσιαστικά «δέκα Νιούτον» ζάχαρη, αλλά μην τη ζητήσετε έτσι από τον παντοπώλη σας!
Σε μία μόνο περίπτωση, η σύγκριση βαρών είναι και σύγκριση μαζών ανεξάρτητα από το βαρυτικό πεδίο (αρκεί όμως να υπάρχει, να μην είναι δηλαδή μηδενικό), και αυτή είναι όταν χρησιμοποιούμε τον κλασικό «Ρωμαϊκό ζυγό» με πρότυπα βάρη (πρότυπες μάζες ουσιαστικά) και όχι ζυγαριά ελατηρίου όπως συνήθως.
Επειδή σε αυτή την περίπτωση, ενδεχόμενη μεταβολή του βαρυτικού πεδίου θα επηρεάσει εξίσου τόσο τις πρότυπες μάζες όσο και τη μετρούμενη μάζα.
Πώς όμως θα μπορούσαμε να μετρήσουμε τη μάζα ενός σώματος ακόμα και σε συνθήκες μικροβαρύτητας? Εφαρμόζοντας μια σταθερή δύναμη και μετρώντας την επιτάχυνσή του!
3. Μεταβολή του βάρους στη Γη.
Όπως προαναφέρθηκε, το βάρος στη Γη εξαρτάται από το τοπικό βαρυτικό πεδίο. Οι διαφορές δεν είναι σημαντικές σε γειτονικές περιοχές, αλλά είναι μεγαλύτερες σε διαφορετικό γεωμετρικό πλάτος, για τους παρακάτω λόγους:
-Η Γη είναι πεπλατυσμένη στους πόλους, άρα όσο κοντύτερα στους πόλους, τόσο πιο κοντά στο κέντρο της Γης που είναι και το κέντρο της βαρύτητας, οπότε η βαρύτητα μεγαλώνει.
-Επίσης, όσο πιο κοντά στους πόλους μειώνεται η κεντρομόλος επιτάχυνση από την περιστροφή της Γης, που είναι μέγιστη στον Ισημερινό.
Άρα η βαρύτητα κοντά στους πόλους αυξάνεται και γι΄αυτόν τον λόγο.
(Για τον ίδιο λόγο, αλλά εδώ ενδιαφέρει η μεγιστοποίηση της γραμμικής ταχύτητας της επιφάνειας της Γης, τα πεδία εκτόξευσης πυραύλων στο Διάστημα βρίσκονται κοντά στον Ισημερινό, και οι τροχιές ακολουθούν ανατολική πορεία).
Φυσικά και το υψόμετρο επηρεάζει το βάρος, καθώς το βαρυτικό πεδίο μειώνεται με την απομάκρυνση από το κέντρο της Γης.
Όμως η αύξηση του υψομέτρου ναι μεν μειώνει τη βαρύτητα, αλλά μειώνει και την πυκνότητα του αέρα, που με τη σειρά της μειώνει την άνωση που υφίσταται ένα σώμα, συνεπώς αυτός ο παράγοντας κάνει το σώμα να "βαραίνει" με το υψόμετρο. Αυτό βέβαια συμβαίνει μέχρι το υψόμετρο των 15km, καθώς από εκεί και πάνω ο αέρας είναι πολύ αραιός για να έχει κάποια ουσιαστική επίδραση στην άνωση.
Σε κάθε περίπτωση πάντως, η επίδραση από τη μείωση της βαρύτητας είναι πολύ μεγαλύτερη από τη μείωση της άνωσης, οπότε τελικά το βάρος του σώματος μειώνεται με το υψόμετρο.
Επίσης, η επίδραση της βαρύτητας της Σελήνης (περισσότερο) και του Ήλιου (λιγότερο) έχουν θεωρητικά επίδραση στο βάρος ενός σώματος, ανάλογα με τη θέση του ως προς αυτά τα ουράνια σώματα, αλλά λέμε θεωρητικά, γιατί η επίδραση αυτή είναι πράγματι πολύ μικρή.
Για παράδειγμα (και εδώ θα χρησιμοποιήσουμε καταχρηστικά και για την ευκολία της κατανόησης των μεγεθών, μονάδες μάζας για να υποδηλώσουμε βάρος), ένας άνθρωπος 70 kg στον Πόλο, θα ζύγιζε 300 gr λιγότερο στον Ισημερινό.
Αντίστοιχα, ένας άνθρωπος 70 kg στη βάση του Έβερεστ θα έχανε περίπου 200 gr μέχρι την κορυφή του εξαιτίας της μείωσης της βαρύτητας, αλλά θα κέρδιζε και γύρω στα 40 gr εξαιτίας της μείωσης της άνωσης της ατμόσφαιρας, άρα συνολικά θα ελάφρυνε κατά 160 gr.
Υπόψην ότι αν κατεβούμε σ’ ένα βαθύ πηγάδι, η τοπική βαρύτητα σε σχέση με τη βαρύτητα στην επιφάνεια του τόπου αυτού μειώνεται, επειδή έχουμε πλέον και μάζα της Γης «πάνω από το κεφάλι μας», που μας τραβά προς τα έξω*.
Συνεπώς, παρόλο που το κέντρο της βαρύτητας της Γης είναι στο κέντρο της, η βαρύτητα στο κέντρο της Γης είναι μηδέν!
*Στην πραγματικότητα, το μέγιστο της βαρύτητας (εικόνα κάτω, μπλε γραμμή) βρίσκεται στο μέσο περίπου της ακτίνας της Γης, εξαιτίας του γεγονότος ότι τα βαθύτερα στρώματα έχουν πολύ μεγαλύτερη πυκνότητα από τα πιο εξωτερικά.
Η "τρύπα της βαρύτητας" είναι μία τεράστια περιοχή μεταξύ Αφρικής και Ινδίας (σκούρο μπλε στον χάρτη επάνω) που αν και γνωστή από το 1948, μόλις το 2023 εξηγήθηκε ότι δημιουργήθηκε από μετακίνηση ηφαιστιακών πετρωμάτων μικρής πυκνότητας κάτω από τον πυθμένα του σημερινού ωκεανού, εκατομμύρια χρόνια πριν. Το αποτέλεσμα είναι και η επιφάνεια του ωκεανού στο κέντρο της περιοχής αυτής* να βρίσκεται περίπου 100m χαμηλότερα σε σχέση με την τυπική στάθμη της θάλασσας.
* Μία περιοχή βέβαια με μέγεθος συγκρίσιμο με αυτό της Ινδίας.
4. Πτώση και βαρύτητα.
Προφανώς η τοπική βαρύτητα προκαλεί τις πτώσεις στα ελεύθερα αντικείμενα, είτε βρίσκονται κοντά στη Γη είτε κοντά σε οποιοδήποτε άλλο ουράνιο σώμα.
Όμως όταν ένας αστροναύτης (μέσα στη στολή του ή μαζί με το σκάφος του) που ΔΕΝ βρίσκονται σε τροχιά, πέφτει ελεύθερα, η βαρύτητα που ο ίδιος νιώθει είναι πρακτικά μηδενική (μικροβαρύτητα).
Έτσι είτε στη Σελήνη πέφτει, είτε στον Δία, είτε σε ακόμα μεγαλύτερο πλανήτη, στη διάρκεια της πτώσης του θα βρίσκεται σε συνθήκες «μικροβαρύτητας».
Αυτό είναι εύκολο να το καταλάβουμε αν αναλογιστούμε ότι η βαρύτητα δρα ομοιόμορφα σε όλα τα μόρια και άτομα που τον αποτελούν, και όχι όπως μέσα σ’ ένα επιταχυνόμενο διαστημόπλοιο που οι δυνάμεις μεταφέρονται στο σώμα του μόνο μέσα από τα σημεία επαφής του με το κάθισμα του διαστημοπλοίου.
Αν λοιπόν κάποτε κατασκευαστεί σύστημα προώθησης με βαρυτικό πεδίο, οι αστροναύτες μπορούν να δεχτούν οσοδήποτε μεγάλη επιτάχυνση (σήμερα έχουν όριο τα 3 - 5g ανάλογα με τη χρονική διάρκεια) και να νοιώθουν ότι βρίσκονται σε μικροβαρύτητα! (Βλέπε και θέμα Νο 80).
5. Γιατί ο Αριστοτέλης είχε άδικο.
Επειδή ο Αριστοτέλης αντιπαθούσε τα πειράματα, και προσπαθούσε να τα ερμηνεύσει όλα με τη λογική.
Έτσι λοιπόν, πίστευε ότι τα βαρύτερα σώματα πέφτουν ταχύτερα προς τη Γη από τα ελαφρύτερα, και το ίδιο δέχονταν όλοι μέχρι την εποχή του Γαλιλαίου, παρότι προφανώς η εμπειρία τους πρέπει να τους έλεγε άλλα*.
Αργότερα όμως, ο Νεύτωνας εισήγαγε τη σχέση a = F / m για την επιτάχυνση, και την F = G x M x m / R2 για την παγκόσμια έλξη.
Στην ελεύθερη πτώση πρόκειται για την ίδια δύναμη και στους δύο τύπους, οπότε αν αντικαταστήσουμε το F του πρώτου τύπου με τον δεύτερο τύπο, θα έχουμε: a = G x M x m / (m x R2), δηλαδή a = G x M / R2, όπου G η παγκόσμια σταθερά, Μ η μάζα της Γης, και R η ακτίνα της.
Είναι λοιπόν φανερό ότι το a, που στην περίπτωση πτώσης προς τη Γη ονομάζεται g, είναι ανεξάρτητο από τη μάζα του σώματος.
Κάτι που ο Γαλιλαίος ερεύνησε πειραματικά με την παρακάτω κατασκευή κεκλιμένου επιπέδου, εφοδιασμένη με καμπανάκια.
*Σε πραγματικές συνθήκες πάντως, δηλαδή λαμβάνοντας υπόψη την αντίσταση του αέρα, μια μεγάλη σφαίρα θα πέσει λίγο νωρίτερα από μια μικρότερη από το ίδιο υλικό, εφόσον πέσουν από αρκετό ύψος.
Αυτό συμβαίνει επειδή στη σφαίρα η μάζα αυξάνεται με την τρίτη δύναμη της ακτίνας, ενώ η επιφάνειά της με τη δεύτερη δύναμη, οπότε στη μικρότερη σφαίρα η επίδραση του αέρα που σχετίζεται με την μετωπική της επιφάνεια είναι αναλογικά σημαντικότερη απ’ ότι στη μεγάλη σφαίρα.
Δέστε και παρακάτω (θέμα Νο 27), σχετικά με το σφαιρικό σχήμα.
Από την άλλη πλευρά, αν χρησιμοποιηθεί για το πείραμα αυτό κεκλιμένο πεδίο, παρότι θεωρητικά δεν θα υπήρχε πρόβλημα οι συνθήκες δεν είναι απόλυτα σωστές, επειδή υπεισέρχεται η ροπή αδράνειας από την περιστροφή των σφαιρών. Για να γίνει σωστά το πείραμα, θα πρέπει οι σφαίρες να τοποθετηθούν σε πανομοιότυπα μικρά "καροτσάκια" που θα κυλάνε με ελάχιστη τριβή.
6. Δράση – Αντίδραση.
Εδώ υπάρχει μια παρανόηση, καθώς συχνά ακούγεται ότι "σε κάθε Δράση αντιστοιχεί μια ίση και αντίθετη Αντίδραση". Η παρανόηση αυτή ξεκίνησε από τη μη ακριβή μετάφραση της διατύπωσης του Νεύτωνα: «Actioni contrariam semper et aequalem esse reactionem» (Σε κάθε δράση αντιστοιχεί πάντοτε μία αντιτιθέμενη ίση αντίδραση).
Ο Νεύτων το έγραψε στα λατινικά και περιγραφικά, και εξάλλου η σωστή μετάφραση του "contrariam" είναι "αντιτιθέμενη" και όχι "αντίθετη", καθώς η έννοια του "αντίθετου" ορίζεται στα μαθηματικά σαφώς.
Μαθηματικά, δύο δυνάμεις (δηλαδή ανυσματικά μεγέθη) είναι είτε ίσες, είτε αντίθετες, δεν μπορεί να είναι και τα δύο ταυτόχρονα!
Και αυτό επειδή στον ορισμό της αντίθετης δύναμης εμπεριέχεται η έννοια του «ίσου μέτρου», όπως εξάλλου και στον ορισμό της ίσης δύναμης.
Άρα η Αντίδραση είναι μια αντίθετη προς τη Δράση δύναμη, ή μία δύναμη ίσου μέτρου και αντίθετης φοράς (ή κατεύθυνσης).
7. Διελκυστίνδα και συγκρούσεις.
Στο γνωστό παιχνίδι της διελκυστίνδας, συχνά αναρωτιόμαστε για τη δύναμη στην οποία υπόκειται το σχοινί.
Χωρίς τη χρήση μαθηματικών, μπορούμε να καταλάβουμε τη λύση με τον παρακάτω απλό τρόπο.
Εφόσον οι ομάδες ισορροπούν, δηλαδή το σχοινί δεν μετακινείται, μπορούμε να καταργήσουμε τη μια ομάδα και να δέσουμε το σχοινί σ’ έναν σταθερό τοίχο.
Το αποτέλεσμα είναι το ίδιο, και είναι πλέον φανερό ότι η δύναμη πάνω στο σχοινί είναι ίση με τη δύναμη που βάζει η (μία μόνο) ομάδα.
Με αντίστοιχο τρόπο μπορούμε να καταλάβουμε ότι η σύγκρουση δύο ίδιων οχημάτων που κινούνται με αντίθετες ταχύτητες, είναι ισοδύναμη (σαν αποτέλεσμα) με τη σύγκρουση του ενός οχήματος που κινείται με την ίδια ταχύτητα, πάνω σ’ έναν άκαμπτο τοίχο.
Εφόσον η σύγκρουση είναι συμμετρική, μπορούμε να φανταστούμε στο σημείο σύγκρουσης μία εύκαμπτη μεμβράνη μεταξύ των αυτοκινήτων, η οποία (θεωρητικά) δεν έχει λόγο να μετακινηθεί κατά τη διάρκεια της σύγκρουσης.
Τώρα αφαιρούμε τη μεμβράνη και την αντικαθιστούμε με έναν άκαμπτο τοίχο, και το αποτέλεσμα για το (ένα) αυτοκίνητο που θα πέσει επάνω του θα είναι το ίδιο.
ΔΕΝ πρέπει να συγχέουμε τα αποτελέσματα της συμμετρικής σύγκρουσης με τη σχετική ταχύτητα προσέγγισης των δύο αυτοκινήτων, που είναι πράγματι διπλάσια από αυτή του ενός αυτοκινήτου.
8. Είναι σταθερές δυνάμεις η Στατική Τριβή και η Αντίδραση;
Η παραπάνω ερώτηση μοιάζει να μην έχει νόημα, καθώς όλοι ξέρουμε ότι η στατική τριβή υπάρχει, αλλιώς πχ δεν θα μπορούσαμε να σταθούμε όρθιοι.
Όμως, η τριβή είναι μία δύναμη που εκδηλώνεται μόνον εφόσον υπάρχει δύναμη που τείνει να κινήσει ένα σώμα, και αντιτίθεται στην κίνησή του μέχρι να πάρει τη μέγιστη τιμή της που προκύπτει από τον γνωστό τύπο υπολογισμού της.
Άρα, αν εφαρμόσουμε μια αυξανόμενη δύναμη πάνω σ’ ένα σώμα που εφάπτεται σ’ένα άλλο, η τριβή αναπτύσσεται ώστε να είναι συνεχώς αντίθετη με την εφαρμοζόμενη δύναμη, μέχρι να φτάσει τη μέγιστη τιμή της, οπότε από εκεί και πέρα το σώμα θα κινηθεί.
Κάτι παρόμοιο συμβαίνει και με την Αντίδραση σε μια εφαρμοζόμενη και αυξανόμενη Δύναμη.
Η Αντίδραση (μιας επιφάνειας πχ) μεταβάλλεται έτσι ώστε να εξισορροπεί κάθε στιγμή τη Δύναμη (Δράση), μέχρι μια μέγιστη τιμή που την καθορίζει η αντοχή της επιφάνειας, μετά την οποία επέρχεται είτε μετακίνηση είτε κατάρρευσή της.
9. «Φυγόκεντρος» δύναμη.
Η φυγόκεντρος δύναμη απλά ... δεν υπάρχει!
Αυτό που ερμηνεύουμε σαν «φυγόκεντρο δύναμη» είναι η αδράνεια, η οποία προσπαθεί να διατηρήσει την ευθύγραμμη κίνηση ενός σώματος το οποίο εξαναγκάζεται σε περιστροφή, όπως ένας δορυφόρος της Γης ή μια πέτρα δεμένη στην άκρη ενός σχοινιού που τη στριφογυρίζουμε.
Η δύναμη που εφαρμόζεται στην πραγματικότητα είναι η κεντρομόλος δύναμη, που είναι αυτή που προκαλεί σ’ ένα σώμα την κεντρομόλο επιτάχυνση, εξαναγκάζοντάς το σε κυκλική τροχιά.
Η «φυγόκεντρος δύναμη» είναι λοιπόν η αντίδραση (αντίθετη δύναμη) στην κεντρομόλο δύναμη, αλλά συνήθως μάς είναι πιο εύκολο να την κατανοήσουμε σαν «δύναμη προς τα έξω», μια και για τις αισθήσεις μας η δράση της είναι πιο προφανής.
10. Η πίεση δεν εφαρμόζεται!
Η πίεση είναι μονόμετρο μέγεθος, οπότε δεν πρέπει να πούμε ότι «εφαρμόζεται» ή «ασκείται», αλλά ότι «υπάρχει» ή «επικρατεί».
Εξαιτίας της πίεσης που επικρατεί λοιπόν, εφαρμόζονται ή ασκούνται δυνάμεις επάνω σε επιφάνειες.
11. Ορμή και Κινητική Ενέργεια.
Με το θεώρημα διατήρησης της ορμής υπολογίζουμε τη μεταβολή της ταχύτητας σωμάτων που συγκρούονται είτε ελαστικά είτε πλαστικά, λαμβάνοντας όμως υπόψη τις ταχύτητες σαν διανυσματικά μεγέθη.
Χρησιμοποιώντας την κινητική ενέργεια μπορούμε να κάνουμε επίσης υπολογισμούς ταχυτήτων, αλλά μόνον εφόσον η κρούση είναι τελείως ελαστική και δεν υπεισέρχεται εξωτερική ενέργεια, αλλιώς ένα μέρος της κινητικής ενέργειας μετατρέπεται σε θερμική και χαλάει το ενεργειακό ισοζύγιο.
Εφόσον όμως μια κρούση είναι τελείως ελαστική, οι εξισώσεις της ορμής και της κινητικής ενέργειας μπορούν να χρησιμοποιηθούν ταυτόχρονα.
Ένα καλό παράδειγμα είναι η εκπυρσοκρότηση ενός όπλου, όπου η ορμή της ανάκρουσης ισούται με την ορμή του βλήματος, αλλά οι κινητικές τους ενέργειες είναι πολύ διαφορετικές, καθώς υπάρχει η ενέργεια της πυρίτιδας που προστίθεται στο σύστημα.
12α. Ροπή και Ισχύς.
Η ροπή είναι πιο κοντά σ’ ένα φυσικό φαινόμενο που μπορούμε να καταλάβουμε, καθώς είναι η στρέψη που εφαρμόζουμε, ή η στρέψη που παίρνουμε από τον άξονα ενός μηχανήματος.
Αν μάλιστα η ροπή είναι αρκετά μεγάλη (και ο άξονας σχετικά λεπτός), μπορούμε να δούμε και οπτικά τα αποτελέσματα της σαν στρεπτική παραμόρφωση στον άξονα. (Βλ και θέμα Νο 49).
Η ισχύς, από την άλλη πλευρά, που είναι η ροπή επί την γωνιακή ταχύτητα, είναι μάλλον ένα λογιστικό μέγεθος, του οποίου τα αποτελέσματα είναι περισσότερο έμμεσα ορατά. (Στην εικόνα επάνω, η κόκκινη καμπύλη είναι η ροπή ενώ η μπλε η ισχύς, ενός βενζινοκινητήρα).
Με την ευκαιρία, στην εικόνα παρακάτω φαίνεται γιατί τα αυτοκίνητα με κινητήρα εσωτερικής καύσης χρειάζονται κιβώτιο ταχυτήτων, ενώ αυτά με ηλεκτροκινητήρα όχι. Η ροπή του ηλεκτροκινητήρα είναι περίπου σταθερή από μηδέν στροφές (πράσινη γραμμή) και μόνο στις υψηλότερες μειώνεται, ενώ του κινητήρα εσωτερικής καύσης έχει ικανοποιητική τιμή σε περιορισμένη περιοχή στροφών, και ουσιαστικά "μεταφέρεται" με τη χρήση διαφορετικών σχέσεων μετάδοσης (υπόλοιπα χρώματα), ώστε να καλύψει όλο το φάσμα της ταχύτητας δρόμου (οριζόντιος άξονας), την οποία επιτρέπει η ισχύς του κινητήρα.
12β. Πόσους ίππους έχει ένα άλογο;
Ακούγεται σαν λογοπαίγνιο, αλλά δεν είναι. Πράγματι η ισχύς ενός ίππου (1HP = 745W) όπως έχει οριστεί από τον James Watt στο τέλος του 18ου αι. (ανύψωση βάρους 550 λιβρών, κατά ένα πόδι, σε ένα δευτερόλεπτο), μοιάζει να είναι αρκετά μικρή σε σχέση με τις δυνατότητες ενός μέσου αλόγου. Και είναι έτσι, επειδή ο Watt υπολόγισε τη μέση δυνατότητα ενός αλόγου σ' έναν 24-ωρο κύκλο, όπου το άλογο θα εργάζονταν συνολικά για 8 ώρες και τις υπόλοιπες θα ξεκουράζονταν. Οπότε τελικά, η ισχύς ενός μέσου αλόγου είναι το τριπλάσιο, δηλαδή, 3HP!
Αυτό εξηγεί και πώς ένας ποδηλάτης πχ, μπορεί να ξεπεράσει την ισχύ του ενός ίππου (1HP) για σύντομα χρονικό διάστημα, ενώ ένα άλογο μπορεί να αποδώσει πάνω από 12ΗΡ για σύντομο διάστημα.
13. Άνωση, ή Άντωση;
Συμβατικά ονομάζουμε άνωση (άνω + ώση) τη δύναμη που ασκούν τα ρευστά σ’ ένα βυθισμένο σώμα, ενώ άντωση (αντί + ώση) τη δύναμη που ασκείται σ’ ένα σώμα που κινείται μέσα σε ρευστό, εξαιτίας της διαταραχής που προκαλείται στο ρευστό. (Βλέπε και θέμα Νο 92).
14. Που οφείλεται η Άντωση σε πτέρυγα;
Συνήθως η άντωση, δηλαδή η δυναμική άνωση σε μία πτέρυγα, εξηγείται με το θεώρημα του Bernoulli, δηλαδή τη διαφορική πίεση που αναπτύσσεται γύρω από την πτέρυγα εξαιτίας της διαφορετικής καμπυλότητας των επιφανειών της.
Η διαφορετική αυτή πίεση όμως δεν αρκεί για να εξηγήσει τις αναπτυσσόμενες δυνάμεις επάνω στην πτέρυγα, ούτε το λόγο που οι συμμετρικές ή επίπεδες πτέρυγες δημιουργούν άντωση.
Η εξήγηση έχει δοθεί από το Ρουμάνο μηχανικό Coanda, που με το ομώνυμο φαινόμενο έδειξε ότι η πτέρυγα, καθώς κινείται με κλίση ως προς τον αέρα, τον επιταχύνει προς τα κάτω και είναι η αντίδραση σ’ αυτή τη δύναμη που ανυψώνει την πτέρυγα.
Το φαινόμενο Bernoulli με τη σειρά του, εξηγεί γιατί η ροή του αέρα προσκολλάται σε κυρτές επιφάνειες, ώστε να «δουλέψει» το φαινόμενο Coanda.
15. Ποδήλατα, νεροχύτες και γυροσκοπικά φαινόμενα.
Επικρατεί η άποψη ότι η ισορροπία στο ποδήλατο οφείλεται στο γυροσκοπικό φαινόμενο των τροχών και ο στροβιλισμός του νερού καθώς αδειάζει ο νεροχύτης στο φαινόμενο Κοριόλις. Και τα δύο είναι λάθος!
Το γυροσκοπικό φαινόμενο των τροχών του ποδηλάτου υπάρχει, αλλά είναι πολύ αδύναμο και όταν το ποδήλατο κινείται με μικρή ταχύτητα, μηδενικό.
Την ισορροπία μας την κρατάμε με μικροδιορθώσεις που κάνουμε ασυναίσθητα με το τιμόνι, το οποίο έχει και φυσική ευστάθεια εξαιτίας της γωνίας Κάστερ που σχηματίζει ο εμπρός τροχός.
Όσο για το νερό στο νεροχύτη, η δύναμη Κοριόλις είναι εντελώς ασήμαντη σ’ αυτή την κλίμακα, η φορά στροβιλισμού του νερού είναι είτε τελείως τυχαία, είτε οφείλεται σε μικροανωμαλίες της επιφάνειας του νεροχύτη.
Αντίθετα, η κίνηση του αέρα στην κλίμακα της Γης (εικόνα), σαφώς επηρεάζεται από τη δύναμη Κοριόλις.
Πάντως, αν τα περίεργα (για τη λογική μας) φαινόμενα που σχετίζονται από την μία πλευρά με τις πολύ μεγάλες ταχύτητες και τις πολύ μεγάλες μάζες, και από την άλλη πλευρά με τα υποατομικά φαινόμενα και σωματίδια, μπορούν να αποδοθούν στο ότι ζούμε σε περιοχή φυσικών φαινομένων πολύ μακριά από τις δύο αυτές περιοχές, το γυροσκοπικό φαινόμενο ίσως είναι το μόνο φυσικό φαινόμενο του άμεσα αισθητού μας κόσμου που είναι εξίσου παράδοξο και αντιβαίνει στην καθημερινή εμπειρία μας. (Βλέπε και θέμα Νο 109).
16. Έλικες και αεριοστρόβιλοι.
Συνήθως κατατάσσουμε τα αεροπλάνα ανάλογα με το σύστημα ώθησής τους, σε ελικοκίνητα και αεριωθούμενα και εξηγούμε με διαφορετικό τρόπο την ώθηση που παράγεται.
Όμως και τα δύο συστήματα στηρίζονται κατά βάση στην αντίδραση της ορμής από την εκτόξευση του αέρα προς τα πίσω, μάλιστα η εκτόξευση αυτή στα σύγχρονα αεριωθούμενα γίνεται σε μεγάλο ποσοστό από πολλαπλά μικρά πτερύγια σαν έλικες, μέσα στο κάλυμμα του κινητήρα (εικόνα).
Η ουσιαστική διαφορά είναι ότι η ταχύτητα του ρεύματος του αέρα από την έλικα περιορίζεται από την ταχύτητα των άκρων των πτερυγίων της, η οποία δεν πρέπει να ξεπεράσει την ταχύτητα του ήχου, γι’ αυτό και οι έλικες χρησιμοποιούνται σε πιο αργά αεροπλάνα.
17. Άνωση και βαρύτητα.
Οι αστροναύτες εκπαιδεύονται μέσα σε δεξαμενές νερού, για να εξοικειωθούν με διάφορες εργασίες σε κατάσταση έλλειψης βαρύτητας.
Παρόλο όμως που οι στολές τους ρυθμίζονται έτσι ώστε να τους προσφέρουν μηδενική πλευστότητα, υπάρχει μια σημαντική διαφορά με την κατάσταση έλλειψης βαρύτητας (μικροβαρύτητας) στην οποία θα βρεθούν όταν μπουν σε τροχιά.
Η άνωση μέσα στο νερό εφαρμόζεται στον «όγκο» που καταλαμβάνει ο αστροναύτης μαζί με τη στολή του.
Ο ίδιος ο αστροναύτης μέσα στη στολή νοιώθει την έλξη τη βαρύτητας, το ίδιο και τα εσωτερικά του όργανα, γι’ αυτό και διατηρεί την αίσθηση του «επάνω και κάτω».
Αυτό βέβαια δεν συμβαίνει σε κατάσταση μικροβαρύτητας, επειδή η έλλειψη της βαρύτητας επηρεάζει ΟΛΑ του τα όργανα και δεν υπάρχει πλέον η αίσθηση του «επάνω και κάτω».
Απλά η δεξαμενή νερού είναι η καλύτερη προσομοίωση, στην επιφάνεια της Γης.
18. Η ταχύτητα του ηλεκτρικού ρεύματος.
Συχνά συγχέουμε την ταχύτητα των ηλεκτρονίων με την ταχύτητα διάδοσης του ηλεκτρικού ρεύματος.
Στην πραγματικότητα η ταχύτητα των ηλεκτρονίων είναι πολύ μικρή (περπατάμε πιο γρήγορα απ’ αυτά!), ενώ η ταχύτητα διάδοσης του ηλεκτρικού ρεύματος πλησιάζει την ταχύτητα του φωτός.
Μπορούμε να φανταστούμε τη σειρά των ηλεκτρονίων σ’ ένα σύρμα πχ, σαν ένα πολύ μακρύ τραίνο στο οποίο από τη στιγμή που θα κινηθεί η μηχανή στο εμπρός μέρος, η μετάδοση της κίνησης στο τελευταίο βαγόνι γίνεται με πολύ μεγάλη ταχύτητα, παρόλο που η ταχύτητα του τραίνου μπορεί να είναι χαμηλή.
Εξάλλου, στο εναλλασσόμενο ρεύμα τα ηλεκτρόνια απλά ταλαντεύονται, χωρίς ουσιαστικά να μετακινούνται.
19α. Πρόσθεση παράλληλων αντιστάσεων.
Όταν υπολογίζουμε την ισοδύναμη αντίσταση παράλληλων αντιστάσεων, θα πρέπει να αναμένουμε ότι η τιμή της θα είναι πάντα μικρότερη από την τιμή της μικρότερης από τις παράλληλες αντιστάσεις (καθώς το ρεύμα περνάει και από άλλες διαδρομές, άρα πιο εύκολα).
Αλλιώς κάπου έχουμε κάνει λάθος στον υπολογισμό!
19β. Γιατί οι τύποι πρόσθεσης πυκνωτών είναι αντίστροφοι από των αντιστάσεων;
Όπως είναι γνωστό ο τύπος πρόσθεσης των αντιστάσεων σε σειρά μοιάζει με τον τύπο πρόσθεσης των παράλληλων πυκνωτών, και αντίστροφα ο τύπος πρόσθεσης παράλληλων αντιστάσεων μοιάζει με τον τύπο πρόσθεσης πυκνωτών σε σειρά.
Εννοείται φυσικά, ότι σε αντίθεση με τις αντιστάσεις, η πρόσθεση των πυκνωτών (και των πηνίων σαν επαγωγών) έχει νόημα μόνο στο εναλλασσόμενο ρεύμα.
Πώς όμως μπορούμε να το καταλάβουμε αυτό, χωρίς τη χρήση τύπων;
Το βασικό που πρέπει να καταλάβουμε είναι ότι η χωρητικότητα συμπεριφέρεται αντίστροφα από την αντίσταση.
Δηλαδή, όσο η τιμή της αντίστασης μεγαλώνει η διέλευση του ρεύματος εμποδίζεται, ενώ όσο η τιμή της χωρητικότητας μεγαλώνει, η διέλευση του ρεύματος διευκολύνεται.
Γενικά τώρα, αν συνδέσουμε δύο στοιχεία σε σειρά, η ένταση του ρεύματος θα μειωθεί, αλλά αν τα συνδέσουμε παράλληλα η ένταση του ρεύματος θα αυξηθεί (επειδή θα μπορεί να περάσει από παράλληλες διαδρομές).
Αλλά ενώ στις αντιστάσεις η μείωση του ρεύματος συνδέεται με αύξηση της αριθμητικής τιμής της συνολικής αντίστασης, στους πυκνωτές συνδέεται με μείωση της αριθμητικής τιμής της συνολικής χωρητικότητάς τους.
Και πώς μειώνεται μία αριθμητική τιμή κάνοντας πρόσθεση; Προσθέτοντας τα αντίστροφά τους, όπως στην περίπτωση των παράλληλων αντιστάσεων.
Μια και το περιλαμβάνει η παραπάνω εικόνα, αντίστοιχη περίπτωση με τις αντιστάσεις είναι και οι επαγωγές (πηνία).
Αλλά (με την ευκαιρία) και η ισχύς βραχυκύκλωσης.
Αλλά και η πρόσθεση των επί μέρους ισχύων βραχυκύκλωσης (για τον προσδιορισμό της τελικής ισχύος βραχυκύκλωσης) ακολουθεί τους τύπους πρόσθεσης των πυκνωτών. Από την ισχύ βραχυκύκλωσης υπολογίζεται η ένταση βραχυκύκλωσης η οποία καθορίζει την αντοχή των συσκευών προστασίας (ασφαλειών και διακοπτών) ώστε να μπορούν να διακόψουν το ρεύμα ενός βραχυκυκλώματος χωρίς να καταστραφούν / εκραγούν.
Συνήθως μας ενδιαφέρει να υπολογίσουμε την ισχύ βραχυκύκλωσης μετά από έναν μετασχηματιστή συν το καλώδιό του, συν ενδεχομένως ένα πηνίο στη γραμμή, συν ενδεχομένως και έναν δεύτερο μετασχηματιστή, εκεί δηλαδή όπου τελικά θα τοποθετήσουμε τη συσκευή προστασίας. Καθώς οι παραπάνω συσκευές συνδέονται σε σειρά, ο τύπος που δίνει την τελική ισχύ βραχυκύκλωσης όταν είναι γνωστές οι επιμέρους τιμές, είναι αυτός των πυκνωτών σε σειρά.
Και αυτό επειδή, όσο μεγαλύτερη η ισχύς βραχυκύκλωσης τόσο μεγαλύτερη είναι η ένταση του ρεύματος, κάτι που όπως είδαμε συμβαίνει και με τους πυκνωτές.
Και κάτι ακόμα.
Είναι γνωστό ότι οι πυκνωτές δεν επιτρέπουν τη διέλευση του συνεχούς ρεύματος (ΣΡ), δεν εμποδίζουν όμως ουσιαστικά το εναλλασσόμενο (ΕΡ). Ένας απλός τρόπος να το καταλάβουμε αυτό είναι ο παρακάτω:
Ας φανταστούμε το ηλεκτρικό ρεύμα σα ροή νερού μέσα από έναν σωλήνα. Το ΣΡ θα ήταν σαν συνεχής ροή, ενώ το ΕΡ σαν παλμική κίνηση. Αν παρεμβάλλουμε σε κάποιο σημείο του σωλήνα έναν πολύ ελαστικό δίσκο (πυκνωτής), τότε η συνεχής ροή του νερού θα εμποδιστεί, δεν θα αποτραπεί όμως η μετάδοση της παλμικής κίνησης του νερού παραπέρα. Ένας εύκολος και σχηματικός τρόπος να το θυμόμαστε, είναι η παρακάτω εικόνα από το ίντερνετ.
20. Πότε καίγονται οι λάμπες.
Θα έχετε παρατηρήσει ότι οι λάμπες πυράκτωσης συνήθως θα καούν (όταν βρίσκονται προς το τέλος της ζωής τους), κάποια στιγμή καθώς τις ανάβετε. Και δεν είναι τυχαίο.
Το νήμα της λάμπας πυράκτωσης είναι μία αντίσταση, και όπως όλες οι αντιστάσεις η τιμή της αυξάνεται με τη θερμοκρασία.
Όταν η λάμπα είναι σβηστή το νήμα είναι κρύο, σε αντίθεση με όταν είναι αναμμένη που φτάνει σε πολύ υψηλή θερμοκρασία, άρα και σε αρκετά ψηλότερη τιμή αντίστασης.
Σύμφωνα όμως με τον νόμο του Ωμ, όσο πιο μικρή η τιμή της αντίστασης, τόσο πιο μεγάλη η ένταση που θα την διαπεράσει (εφόσον εφαρμόζεται η ίδια τάση).
Έτσι λοιπόν, τη στιγμή του ανάμματος της λάμπας τη διαπερνά αρκετά μεγαλύτερα ένταση από την κανονική της, και εφόσον το νήμα της είναι ήδη καταπονημένο από πολλές ώρες λειτουργίας, προκαλείται το κάψιμό του.
21. Τάση και Ένταση του ηλεκτρικού ρεύματος. Ποια είναι πιο επικίνδυνη;
Κατ’ αρχήν θα πρέπει να θυμίσουμε ότι η ένταση του ηλεκτρικού ρεύματος μοιάζει με τη ροή ενός ποταμού. Όσο περισσότερο το νερό, τόσο μεγαλύτερη η ένταση.
Αντίστοιχα η τάση μοιάζει με την ορμητικότητα ενός ποταμού, όσο πιο ορμητικός τόσο μεγαλύτερη τάση.
Τέλος, η ισχύς της πηγής του ηλεκτρισμού μοιάζει με το μέγεθος της λίμνης ενός φράγματος, που τροφοδοτεί ένα ποτάμι. Όσο μεγαλύτερη η λίμνη, τόσο περισσότερο νερό μπορεί να δώσει, χωρίς να επηρεαστεί η στάθμη της.
Το όριο λοιπόν της βλάβης που προκαλεί το ηλεκτρικό ρεύμα στον άνθρωπο καθορίζεται από την έντασή του, και βρίσκεται χοντρικά στα 30 mA.
Όμως, η ένταση η οποία θα διαπεράσει το ανθρώπινο σώμα εξαρτάται από την τάση του ρεύματος και την αντίσταση του ανθρώπινου σώματος, σύμφωνα με τον γνωστό νόμο του Ωμ.
Η αντίσταση του ανθρώπινου σώματος βρίσκεται γύρω στα 1850 Ω, οπότε εφαρμόζοντας τον νόμο του Ωμ για τα 30 mA (0.03 A), έχουμε:
Τάση = 1850 Ω Χ 0.03 Α = περίπου 50 V, που είναι και το όριο της τάσης ασφαλείας για τα ηλεκτρικά κυκλώματα.
Αυτή είναι όμως η μισή ιστορία!
Η άλλη μισή είναι ότι σε περίπτωση υψηλότερης τάσης, η ισχύς της πηγής θα πρέπει να είναι αρκετή για να υποστηρίξει τη ροή των 30 mA, για να γίνει επικίνδυνη.
Για παράδειγμα, η τάση του κυκλώματος υψηλής τάσης του αυτοκινήτου είναι μεγαλύτερη από 10.000 V, αλλά η ισχύς του είναι περιορισμένη και το «χτύπημα» από ένα ενεργό μπουζοκαλώδιο πχ, είναι επώδυνο αλλά όχι θανατηφόρο.
Ο στατικός ηλεκτρισμός από την τριβή μας με συνθετικό ή μάλλινο ύφασμα μπορεί επίσης να φθάσει τα 10.000 V σε τάση, αλλά δεν μπορεί να δώσει αρκετή ένταση ώστε να γίνει κάτι περισσότερο από ενοχλητικός.
Αντίθετα, το οικιακό ρεύμα των 230 V είναι σαφώς θανατηφόρο, καθώς τροφοδοτείται από όλο το δίκτυο της ΔΕΗ.
Εδώ να διευκρινίσουμε ότι οι ασφάλειες στον ηλεκτρικό πίνακα έχουν αρκετά μεγάλη τιμή (τουλάχιστον 6 Α), οπότε ΔΕΝ μας προστατεύουν καθόλου από τα αποτελέσματα ενδεχόμενης επαφής μας με την οικιακή τάση.
Το μόνο που μας προστατεύει είναι το ειδικό ρελέ εναντίον της ηλεκτροπληξίας (που πλέον είναι υποχρεωτικό για όλες τις ηλεκτρικές εγκαταστάσεις), το οποίο ενεργοποιείται στα 30 mA και διακόπτει ακαριαία το ηλεκτρικό κύκλωμα.
22. Ενεργή (πραγματική) και Άεργος Ισχύς, και Ενέργεια.
Αναφερόμαστε φυσικά στο Εναλλασσόμενο Ρεύμα, το οποίο επικράτησε στον «πόλεμο των ρευμάτων», έναντι του Συνεχούς Ρεύματος (βλέπε και το άρθρο DC vs AC, στο ίδιο blog).
Το εναλλασσόμενο ρεύμα έχει την ιδιομορφία να περνάει από πυκνωτές και από πηνία, αντιμετωπίζοντας σε κάθε περίπτωση κάποια αντίσταση, ενώ για το συνεχές ρεύμα ο (ιδανικός) πυκνωτής είναι ανοικτό κύκλωμα και το (ιδανικό) πηνίο βραχυκύκλωμα.
Όμως η αντίσταση που προβάλλουν οι πυκνωτές και τα πηνία στο εναλλασσόμενο ρεύμα, δεν είναι σαν την ωμική αντίσταση, που θερμαίνεται.
Οι (ιδανικοί) πυκνωτές και πηνία δεν θερμαίνονται, και συμπεριφέρονται σαν «άεργες» αντιστάσεις στο κύκλωμα, καθώς αποθηκεύουν και εναλλάσσουν με την πηγή τροφοδοσίας ενέργεια, είτε σε μορφή ηλεκτρικού πεδίου (οι πυκνωτές), είτε σε μορφή μαγνητικού πεδίου (τα πηνία).
Όταν λοιπόν στο κύκλωμά μας υπάρχουν πυκνωτές ή συνηθέστερα πηνία (όπως στα σώματα φθορισμού πχ), κυκλοφορεί ένα επιπλέον ρεύμα που δεν παράγει πραγματικό έργο, δεν παύει όμως να «φορτώνει» τα καλώδια.
Αυτό το «άεργο» ρεύμα όμως και η κατά συνέπεια «άεργη» ισχύς και ενέργεια που αντιπροσωπεύει, δεν μετριόνται από τον μετρητή ενέργειας της ΔΕΗ, ο οποίος μετράει μόνο την «πραγματική» ισχύ και ενέργεια που καταναλώνουν τα ωμικά φορτία, όπως οι λάμπες πυράκτωσης, ο θερμοσίφωνας, η ηλεκτρική κουζίνα, τα ηλεκτρικά θερμαντικά σώματα, κλπ.
Ειδικότερα, οι ηλεκτρικοί κινητήρες επειδή έχουν πηνία αλλά παράγουν και πραγματικό έργο (αλλιώς πώς θα έπλενε το πλυντήριο?), καταναλίσκουν τόσο άεργη όσο και πραγματική ενέργεια.
Να επισημάνουμε με την ευκαιρία, ότι κάποιες συσκευές που κυκλοφορούν στο εμπόριο για να μπουν στην πρίζα και υπόσχονται μείωση του λογαριασμού του ρεύματος, ΔΕΝ δουλεύουν.
Οι συσκευές αυτές έχουν πυκνωτές που (καθώς η δράση τους είναι αντίθετη με αυτή των πηνίων) μειώνουν πράγματι την ένταση του ρεύματος, αλλά επιδρούν ΜΟΝΟ στο κομμάτι της έντασης που αντιστοιχεί στην άεργη ενέργεια, και που όπως προαναφέρθηκε ΔΕΝ μετριέται από τον μετρητή ενέργειας της ΔΕΗ.
23. Mια αντίσταση διαφορετική από τις άλλες.
Θα έχετε ακούσει ότι τα συνηθισμένα κυλινδρικά (ομοαξονικά) καλώδια της τηλεόρασης έχουν αντίσταση 75 Ω, και μάλιστα χωρίς η αντίσταση αυτή να αναφέρεται σε συγκεκριμένο μήκος τους.
Αυτό συμβαίνει επειδή στις υψηλές συχνότητες (μεγαλύτερες από 100 kHz), αυτό που προκαλεί την εξασθένιση του ηλεκτρικού σήματος* δεν είναι η συνηθισμένη ωμική αντίσταση του καλωδίου, αλλά η κυματική ή σύνθετη αντίστασή του, που εξαρτάται από τα γεωμετρικά στοιχεία της διατομής του και το μονωτικό υλικό.
Η σύνθετη αυτή αντίσταση έχει επίσης σαν μονάδα το Ωμ, και για τα καλώδια της τηλεόρασης έχει τυποποιηθεί στα 75 Ω, καθώς είναι σημαντικό το καλώδιο να τερματίζει σε υποδοχή με την ίδια σύνθετη αντίσταση, ώστε να μην υπάρχουν ανακλάσεις (και απώλεια ισχύος) του ηλεκτρομαγνητικού κύματος.
Σε υψηλότερες συχνότητες μάλιστα όπως στα ραντάρ, τα ηλεκτρομαγνητικά κύματα δεν χρειάζεται καν συμπαγή αγωγό, αλλά ένας κούφιος μεταλλικός σωλήνας που ονομάζεται κυματοδηγός κάνει μια χαρά τη δουλειά.
*Σε αυτές τις ψηλές συχνότητες, η ισχύς που μεταφέρεται είναι σε μορφή ηλεκτρομαγνητικού κύματος και είναι σχετικά χαμηλή, ενώ είναι συνήθως το σήμα (δηλαδή η πληροφορία) που μεταφέρεται, αυτό που μας ενδιαφέρει. Υπάρχουν βέβαια και εξαιρέσεις όπως ο φούρνος μικροκυμάτων, όπου εκεί αξιοποιείται αυτή καθαυτή η ισχύς της ηλεκτρομαγνητικής ακτινοβολίας.
24. Τα όρια της Ατμόσφαιρας, του Διαστήματος και της Βαρύτητας.
Το όριο της ατμόσφαιρας (και η αρχή του Διαστήματος) έχει οριστεί στα 100 km πάνω από την επιφάνεια της Γης, με το σκεπτικό ότι η ατμόσφαιρα στο ύψος αυτό είναι τόσο αραιή, ώστε για να διατηρήσει την πτήση του ένα αεροπλάνο (προφανώς πυραυλοκίνητο) θα πρέπει ουσιαστικά να τεθεί σε τροχιά, για την οποία απαιτείται ταχύτητα τουλάχιστον 28.000 km/h. (Η ταχύτητα τροχιάς δεν πρέπει να συγχέεται με την ταχύτητα διαφυγής από τη Γη, που είναι 40.300 km/h).
Για σύγκριση, ο Διεθνής Διαστημικός Σταθμός περιστρέφεται γύρω στα 400 km πάνω από την επιφάνεια της Γης. Δεν πρέπει όμως να συγχέεται η ύπαρξη ατμόσφαιρας με την ύπαρξη βαρύτητας, τα δύο είναι τελείως άσχετα μεταξύ τους!
Αν και η ατμόσφαιρα ουσιαστικά τελειώνει στα 100 km πάνω από τη Γη (με τη μισή πυκνότητά της να βρίσκεται στα 5 πρώτα km), η βαρύτητα της Γης επεκτείνεται πολύ περισσότερο (μειούμενη φυσικά γρήγορα με την απόσταση) αλλά φθάνει τουλάχιστον μέχρι τη Σελήνη, αφού την κρατάει σε τροχιά!
Ο άνθρωπος μπορεί να ζήσει μεγάλο διάστημα χωρίς βαρύτητα, αλλά μόνο 1-2 λεπτά χωρίς ατμόσφαιρα, καθώς θα πεθάνει από έλλειψη οξυγόνου (δεν σκάει πάντως σαν μπαλόνι!)
Γενικότερα, η επίδραση της βαρύτητας ενός ουράνιου σώματος καθορίζεται από τον συνδυασμό της μάζας του και της απόστασής του από άλλα ουράνια σώματα, και η εμβέλειά της εκφράζεται με την ακτίνα της "σφαίρας του Hill" γύρω απ' αυτό.
Στο παρακάτω διάγραμμα φαίνεται η ακτίνα Hill (σε km, σε λογαριθμική κλίμακα) των πλανητών του Ηλιακού Συστήματος (και κάποιων νάνων πλανητών). Από το διάγραμμα προκύπτει ότι η Σελήνη είναι σαφώς μέσα στη σφαίρα Hill της Γης, αλλά τη μεγαλύτερη σφαίρα Hill την έχει ο Ποσειδώνας (Neptun) παρότι δεν είναι ο μεγαλύτερος πλανήτης, εξαιτίας της μεγάλης απόστασής του από τον Ήλιο.
25. Ποιά είναι η θερμοκρασία του Διαστήματος;
Φυσικά ξέρουμε ότι η ελάχιστη δυνατή θερμοκρασία, όπου παύει κάθε κίνηση των μορίων είναι -273 βαθμοί Κελσίου, και ένα σώμα που θα αφεθεί στο Διάστημα για αρκετό χρόνο προστατευμένο τελείως από την ακτινοβολία του Ήλιου θα πλησιάσει αυτή τη θερμοκρασία, καθώς βαθμιαία θα ακτινοβολήσει όλη τη θερμότητά του.
Καθώς όμως το κενό είναι το τέλειο μονωτικό, αυτή είναι η μοναδική διαδικασία με την οποία το σώμα θα χάσει θερμότητα, οπότε χρειάζεται αρκετός χρόνος και δεν συμβαίνει ταχύτατα όπως εμφανίζεται σε κάποιες κινηματογραφικές ταινίες. (Βλέπε και θέμα Νο 93).
26. Ποια είναι η πρωταρχική πηγή των ανανεώσιμων πηγών ενέργειας;
Όλες οι ανανεώσιμες πηγές ενέργειας στη Γη, έχουν μόνο δύο πρωταρχικές πηγές:-Την Ηλιακή ενέργεια (που είναι η αιτία για τη φωτεινή, επιφανειακή θερμική, αιολική, των κυμάτων, φωτοσύνθεσης άρα και των καυσίμων κλπ), και
-Τη Γεωθερμική ενέργεια. Μάλιστα η ενέργεια αυτή προέρχεται κατά περίπου 50% από την υπολειπόμενη θερμότητα δημιουργίας της Γης που κρατάει ακόμα διάπυρο τον πυρήνα της, και κατά 50% από την Αργή Ραδιενεργή Διάσπαση που συμβαίνει με φυσικό τρόπο στα ραδιενεργά στοιχεία των μεσαίων και εξωτερικών στρωμάτων της Γης (Μανδύας και Λιθόσφαιρα).
27. Το σφαιρικό σχήμα.
Η σφαίρα είναι το σχήμα που για δεδομένο όγκο έχει τη μικρότερη επιφάνεια.
Αντίστοιχα, ο κύκλος για δεδομένη επιφάνεια έχει την μικρότερη περίμετρο.
Επειδή λοιπόν τα υγρά, και ιδιαίτερα το νερό παρουσιάζουν επιφανειακή τάση, σταγόνες ή ποσότητες νερού σε συνθήκες μικροβαρύτητας παίρνουν τέλειο σφαιρικό σχήμα, εφόσον φυσικά παραμένουν αδιατάρακτες.
Επίσης, το σφαιρικό σχήμα είναι αυτό που παρουσιάζει τις μικρότερες θερμικές απώλειες (εφόσον αυτό είναι κάτι που μας ενδιαφέρει) και αυτή η ιδιότητα γίνεται τόσο πιο έντονη όσο μεγαλώνει η διάμετρος της σφαίρας, καθώς ο όγκος της (από τον οποίο εξαρτάται η θερμοχωρητικότητα) είναι ανάλογος με τον κύβο της ακτίνας της, ενώ η επιφάνειά της (από την οποία γίνεται η ανταλλαγή θερμότητας) από το τετράγωνό της.
Αυτός είναι και ένας από τους λόγους* που οι μικρότεροι από τη Γη γαιώδεις πλανήτες και δορυφόροι (όπως ο Άρης και η Σελήνη) έχουν ψυχθεί σε βάθος, ταχύτερα από τη Γη.**
Αλλά και ο λόγος που οι μικρές χιονόμπαλες λιώνουν με ταχύτερο ρυθμό από τις μεγαλύτερες!
Αλλά και ο λόγος που οι μικρές χιονόμπαλες λιώνουν με ταχύτερο ρυθμό από τις μεγαλύτερες!
Αντίστροφα, όσο μια συγκεκριμένη μάζα διασκορπίζεται σε μικρότερα κομμάτια (σφαιρικά ή όχι), η συνολική εξωτερική επιφάνειά της αυξάνεται κατά πολύ, με αποτέλεσμα να ψύχεται πολύ ταχύτερα αλλά και να αναφλέγεται πολύ πιο εύκολα και έντονα, καθώς πολύ μεγαλύτερη επιφάνεια έρχεται σε επαφή με το οξυγόνο της ατμόσφαιρας.
Αυτός είναι και ο λόγος που τα υγρά καύσιμα καίγονται ταχύτατα όταν είναι σε διασκορπισμό, αλλά και σκόνη από σιτηρά ή ακόμα και κοινή σκόνη μπορεί να αναφλεγεί εκρηκτικά κάτω από ορισμένες συνθήκες.
* Ένας άλλος λόγος είναι ότι η Γη θερμαίνεται και από την αργή πυρηνική διάσπαση των ραδιενεργών τμημάτων των πετρωμάτων της.
** Η σχετικά γρήγορη στερεοποίηση μεγάλου μέρους του πυρήνα τους, είχε σαν αποτέλεσμα να εξαφανιστεί το μαγνητικό τους πεδίο, που με τη σειρά του επέτρεψε στον ηλιακό άνεμο να «σαρώσει» την ατμόσφαιρά τους, και στη συνέχεια να χάσουν το νερό που είχαν σε υγρή μορφή.
28. Γιατί δεν έχει νόημα το Αεικίνητο.
Φυσικά το Αεικίνητο δεν έχει κατασκευαστεί, ούτε θα κατασκευαστεί ποτέ.
Κάποιες συσκευές επίδειξης που μοιάζουν με «Αεικίνητα», είτε παίρνουν ενέργεια από το περιβάλλον, είτε την έχουν αποθηκευμένη.*
Όμως, ακόμα και αν μπορούσε να κατασκευαστεί ένα Αεικίνητο, δεν θα ήταν τίποτα περισσότερο από μια αξιοπερίεργη μηχανή σ’ ένα μουσείο, καθώς θα μπορούσε μόνο να συντηρήσει την κίνησή της, αλλά θα σταματούσε αμέσως αν θα έπρεπε να δώσει ωφέλιμη ισχύ.
Οπότε πόσο απέχει ένα Αεικίνητο με (θεωρητική) απόδοση 100%, από τις σύγχρονες μεγάλες γεννήτριες, κινητήρες και μετασχηματιστές, που έχουν πραγματική απόδοση που πλησιάζει το 99%?
* Δύο τέτοιες συσκευές είναι, η πρώτη το "ηλεκτρικό κουδούνι της Οξφόρδης" εικόνα κάτω, που δουλεύει από το 1840 με ηλεκτροστατικό τρόπο, τροφοδοτούμενο από δύο ξηρές ηλεκτρικές στήλες υψηλής τάσης σε σειρά.
Η δεύτερη συσκευή είναι το Beverly clock (από το όνομα του κατασκευαστή του), που βρίσκεται σε πανεπιστήμιο της Νέας Ζηλανδίας. Αν και μοιάζει με συμβατικό εκκρεμές της εποχής του, δεν χρειάστηκε ποτέ κούρδισμα από το 1864 που κατασκευάστηκε! Το μυστικό του βρίσκεται σ' έναν αεροστεγή θάλαμο 28 λίτρων που ένα τμήμα του διαθέτει μία μεταλλική μεμβράνη, η οποία μετακινείται ελαφρά καθώς η θερμοκρασία και η πίεση του αέρα μεταβάλλονται. Αυτή η κίνηση μετατρέπεται από κατάλληλο μηχανισμό σε ένα πολύ μικρό αλλά συχνά επαναλαμβανόμενο κούρδισμα.
29. Καλή ταλάντωση εναντίον κακής ταλάντωσης.
Όταν μια ταλάντωση είναι ενοχλητική ή επιβλαβής και πρέπει να αποσβεστεί, δύο είναι οι μέθοδοι:
-Να απορροφήσουμε με «φρενάρισμα» την ενέργειά της μετατρέποντάς την σε θερμότητα, όπως πχ στα αμορτισέρ των αυτοκινήτων.
-Να την εξουδετερώσουμε με μια ταλάντωση ίσης συχνότητας, αλλά αντίθετης φάσης. Έτσι, εκεί όπου η αρχική ταλάντωση έχει κορυφή, η νέα ταλάντωση θα έχει βύθιση, οπότε το άθροισμά τους θα δώσει μια πολύ μειωμένη ή και μηδενική ταλάντωση (εικόνα).
Ο πρώτος τρόπος είναι ο πιο εύκολος και διαδεδομένος και επίσης είναι αυτός που χρησιμοποιεί η Φύση, ενώ ο δεύτερος χρησιμοποιείται από τη μοντέρνα τεχνολογία και εφαρμόζεται σε «ενεργές» ωτοασπίδες, μείωση ταλάντευσης ουρανοξυστών κλπ.
30. Μικροσκόπια και τηλεσκόπια.
Όλοι γνωρίζουμε τι είναι τα μικροσκόπια και τα τηλεσκόπια, και πώς χρησιμοποιούνται.
Όμως τα μικροσκόπια έχουν ένα πλεονέκτημα έναντι των τηλεσκοπίων στο να αυξάνουν την ικανότητα του ματιού, που βασίζεται στο ότι πολύ μικρά αντικείμενα μπορεί να «φωτιστούν» και με δέσμη ηλεκτρονίων (στα ηλεκτρονικά μικροσκόπια), ώστε ουσιαστικά να μπορούμε να δούμε σε ατομικό μέγεθος.
Έτσι, με τα ηλεκτρονικά μικροσκόπια μπορούμε να δούμε 700.000 φορές μικρότερα αντικείμενα απ’ ότι με το γυμνό μάτι, ενώ με τα ισχυρότερα τηλεσκόπια μόνο 6.000 φορές λιγότερο λαμπρά αντικείμενα, απ’ ότι με το γυμνό μάτι.
31. Η φωνή του «Ντόναλτ Ντακ».
Θα έχετε ενδεχομένως δει ή μάλλον ακούσει, ότι η φωνή κάπου που έχει μόλις πάρει μια αναπνοή με αέριο ήλιο, λεπταίνει με ένα μάλλον αστείο τρόπο, θυμίζοντας τη φωνή του Ντόναλτ Ντακ.
Αυτό συμβαίνει επειδή η ταχύτητα διάδοσης των ηχητικών κυμάτων στο ήλιο είναι 2.5 φορές μεγαλύτερη απ’ ότι στον αέρα, εξαιτίας της πολύ μικρότερης πυκνότητάς του, με αποτέλεσμα ο ήχος να μεταδίδεται με μεγαλύτερη ταχύτητα και να συντονίζεται σε ψηλότερες συχνότητες.
Έτσι όταν έχουμε αναπνεύσει ήλιο, οι ψηλότερες συχνότητες της φωνής μας συντονίζονται και ενισχύονται μέσα στη στοματική μας κοιλότητα πολύ περισσότερο από τις χαμηλότερες, με αποτέλεσμα η φωνή μας να ακούγεται πιο «λεπτή».
Ο Ντόναλτ Ντακ πάντως δεν αναπνέει ήλιο, αλλά (σαν πάπια) έχει λεπτότερες χορδές και μικρότερη στοματική κοιλότητα (αντηχείο) από του ανθρώπου.
Αντίστροφα, αν πάρει κανείς μια αναπνοή με το αέριο SF6 (χρησιμοποιείται σαν μονωτικό στους διακόπτες υψηλής τάσης), που είναι 6 φορές πυκνότερο από τον αέρα, η φωνή του «βαραίνει» και ακούγεται σαν του Darth Vader.
32. Το παράδοξο με την ταχύτητα του φωτός.
Η Γυμνασιακή Φυσική διδάσκει ότι εάν βρισκόμαστε σ’ ένα όχημα που κινείται ευθύγραμμα με ταχύτητα πχ 50 km/h, και ρίξουμε προς τα εμπρός ένα βέλος που φεύγει από το τόξο με ταχύτητα 150 km/h, η ταχύτητα του βέλους ως προς το έδαφος (πριν τουλάχιστον αρχίσει να μειώνεται από την αντίσταση του αέρα), θα είναι 200 km/h.
Αν όμως βρισκόμαστε μέσα σ’ ένα πολύ γρήγορο διαστημόπλοιο που κινείται με την μισή πχ ταχύτητα του φωτός (δεν προβλέπεται πάντως να κατασκευαστεί σύντομα!) και ρίξουμε μια φωτεινή ακτίνα από το εμπρός παράθυρο προς την κατεύθυνση κίνησης, τότε τόσο ο αστροναύτης (λογικό), όσο και ένας εξωτερικός παρατηρητής (όχι τόσο λογικό), θα «δουν» τα φωτόνια της ακτίνας να κινούνται ακριβώς με την ταχύτητα του φωτός.
Δηλαδή η ταχύτητα του φωτός, ΔΕΝ προστίθεται στην ταχύτητα που διαστημοπλοίου για τον εξωτερικό παρατηρητή*.
Αυτό είναι μία από τις συνέπειες της θεωρίας της Σχετικότητας, οι οποίες μοιάζουν να έρχονται σε αντίθεση με την κοινή λογική, και η οποία φυσικά βασίζεται στην εμπειρία μας.
Όμως η θεωρία της Σχετικότητας ισχύει πάντα, απλά η επίδρασή της είναι ασήμαντη για τις ταχύτητες της καθημερινότητάς μας, γι’ αυτό και οι συνέπειές της είχαν περάσει απαρατήρητες μέχρι σχετικά πρόσφατα.
* Η συχνότητα όμως της φωτεινής ακτινοβολίας που βλέπει ο εξωτερικός παρατηρητής επηρεάζεται από την ταχύτητα του διαστημοπλοίου (φαινόμενο Doppler) και αυτό μας επιτρέπει να μετράμε την ταχύτητα απομάκρυνσης των άστρων και των γαλαξιών από το Ηλιακό μας σύστημα, και μάλιστα με αυτόν τον τρόπο έχει βρεθεί ότι το Σύμπαν διαστέλλεται.
33. Θα μπορέσουμε ποτέ να ξεπεράσουμε την ταχύτητα του φωτός;
Όχι!, γιατί τότε ο χρόνος θα έπρεπε να κυλά ανάποδα και επίσης θα έπρεπε να ξεπεράσουμε την άπειρη αδράνεια των σωμάτων!
Μια από τις συνέπειες της θεωρίας της Σχετικότητας είναι ότι όταν κάτι «υλικό» πλησιάζει την ταχύτητα του φωτός, ο χρόνος για τον εξωτερικό παρατηρητή επιβραδύνεται (και η αδράνεια του «υλικού» αυξάνεται, αλλά γι’ αυτό παρακάτω) και αν θα μπορούσαμε να φτάσουμε ακριβώς στην ταχύτητα αυτή, η ροή του χρόνου θα σταμάταγε τελείως.
Μέχρι τώρα τίποτα δεν έχει έλθει σε αντίφαση με αυτή την αρχή, το αντίθετο μάλιστα όλες οι μέχρι τώρα παρατηρήσεις την έχουν επιβεβαιώσει, και αν σε κάποιες περιπτώσεις υπήρξε αμφιβολία, ακριβέστερες μετρήσεις εντόπισαν το λάθος.
Σε μία μόνο περίπτωση μοιάζει να έχει γίνει υπέρβαση της ταχύτητας του φωτός και αυτό συνέβη αμέσως μετά τη Δημιουργία του Σύμπαντος (Big Bang), όταν στιγμιαία το Σύμπαν επεκτάθηκε πάρα πολύ γρήγορα.
Όμως, οι επιστήμονες κατέληξαν ότι η επέκταση εκείνη έγινε με τη δημιουργία νέου χώρου, οπότε το παγκόσμιο ρεκόρ της ταχύτητας εξακολουθεί και ανήκει στο φως, όταν κινείται στο κενό.
Όταν οι συνέπειες της (υποθετικής) υπέρβασης της ταχύτητας του φωτός έγιναν γνωστές στις αρχές του 20ου αιώνα, σατιρίστηκαν με τους παρακάτω στίχους (η μετάφραση από παλιά ελληνική έκδοση σειράς βιβλίων του περιοδικού LIFE):
«Ήταν μια κομψή κυρία που εγνώριζε σαφώς
πώς να ταξιδεύει μόνη, γρηγορότερα απ’ το φως.
Εξεκίνησε μια μέρα - κατευόδειο καλό της-
και επέστρεψε ξανά - να τι είναι η Σχετικότητης-
την προηγουμένη νύχτα πίσω πάλι στο χωριό της!»
34. Οδηγίες για μελλοντικούς ... Jedi.
Μία από τις συνέπειες της κίνησης σε ταχύτητες κοντά στην ταχύτητα του φωτός είχε διατυπωθεί ήδη πριν τον Αϊνστάιν από τους Lorentz και FitzGerald (το κεφαλαίο G δεν είναι λάθος), και αφορά στη συστολή του μήκους κατά τη φορά της κίνησης, στις ταχύτητες αυτές.
Δεν είναι λοιπόν καθόλου περίεργο, που ο Τύπος της εποχής σατίρισε την ανακάλυψη αυτή με τους παρακάτω στίχους (η μετάφραση από παλιά ελληνική έκδοση σειράς βιβλίων του περιοδικού LIFE):
«Ήτανε ένας νέος σπουδαίος στο σπαθί
κανένας δεν μπορούσε να του αντισταθεί
στα χέρια του το ξίφος πετούσε σαν πουλί.
Του Φίτζεραλντ και Λόρεντζ όμως η συστολή
τον κάναν άνω κάτω, και τ’ ακριβό σπαθί
να μοιάζει μ’ ένα ...πιάτο!»
Και μπορεί εκείνη την εποχή να ήταν σάτιρα, στη μελλοντική εποχή των ... Jedi όμως τίποτα δεν αποκλείεται, και οι ικανότεροι στο φωτόσπαθο του είδους τους, θα πρέπει μάλλον να το λάβουν σοβαρά υπόψη!
35. Αύξηση της «μάζας» κοντά στην ταχύτητα του φωτός.
Η εξίσωση της μάζας στη θεωρία της Σχετικότητας, δείχνει αύξησή της όσο η ταχύτητά της πλησιάζει την ταχύτητα του φωτός.
Αυτό δεν σημαίνει όμως ότι η μάζα «φουσκώνει», αλλά ότι η αδράνειά της αυξάνεται.
Όσο δηλαδή επιταχύνεται μια μάζα και πλησιάζει την ταχύτητα του φωτός, η δύναμη που χρειάζεται για να την επιταχύνει λίγο ακόμα αυξάνεται με τρομακτικό ρυθμό, με αποτέλεσμα να μην υπάρχει δύναμη αρκετά μεγάλη στο Σύμπαν για να της προσδώσει ακριβώς την ταχύτητα αυτή.
Γι’ αυτό και στους επιταχυντές σωματιδίων χρειάζονται τεράστια μηχανήματα και ανάλογη ισχύς, για να επιταχύνουν μερικά υποατομικά σωματιδίων πολύ κοντά αλλά όχι ακριβώς, στην ταχύτητα του φωτός.
36. Επίδραση της ταχύτητας και της μάζας στον χρόνο.
Στην εικόνα, φαίνεται η επίδραση της ταχύτητας και της απομάκρυνσης από το κέντρο της Γης, στον χρόνο στο εσωτερικό ενός διαστημοπλοίου. Ένα διαστημόπλοιο για να διατηρηθεί σε χαμηλή τροχιά (ακτίνας από το κέντρο της Γης περίπου 7000 km), πρέπει να έχει μία ταχύτητα που του δίνει μία επιβράδυνση στον χρόνο (μπλε γραμμή) κατά 30 μs/24h. Σε αυτό το ύψος η επίδραση της βαρύτητας στον χρόνο (πράσινη γραμμή) είναι πρακτικά μηδενική. Σε τροχιά ακτίνας γύρω στα 10.000 km (δηλ. 3500 km πάνω από την επιφάνεια της Γης) η επίδραση της ταχύτητας και της βαρύτητας αλληλοαναιρούνται (κόκκινη γραμμή). Στο ύψος των δορυφόρων GPS όμως, προκύπτει μία σαφής επιτάχυνση του χρόνου, η οποία μεγαλώνει λίγο ακόμα για τους γεωστατικούς δορυφόρους που κινούνται ακόμα ψηλότερα. Είναι φανερό όμως, ότι αυτή η επιτάχυνση στον χρόνο δεν μπορεί να ξεπεράσει ουσιαστικά τα 50 μs/24h, για αντικείμενα σε τροχιά γύρω από τη Γη.
Είναι φανερό ότι τα συστήματα GPS πρέπει να μετρούν με πολύ μεγάλη ακρίβεια τους χρόνους διαδρομής των ηλεκτρομαγνητικών σημάτων από τους δορυφόρους, για να προσδιορίζουν την απόσταση (και τελικά τη θέση) του παρατηρητή με ικανοποιητική ακρίβεια.
Για να υπάρχει όμως η ακρίβεια αυτή, θα πρέπει να ληφθεί υπόψη τόσο η ταχύτητα των δορυφόρων GPS, όσο και απόστασή τους από τη Γη, επειδή οι δύο αυτοί παράγοντες επηρεάζουν το χρονικό πλαίσιο των ηλεκτρομαγνητικών κυμάτων σύμφωνα με τη θεωρία της Σχετικότητας.
Όσο πιο μεγάλη η ταχύτητα και όσο πιο μεγάλη η βαρύτητα, τόσο ο χρόνος για τα ηλεκτρομαγνητικά κύματα διαστέλλεται (καθυστερεί).
Έχει βρεθεί λοιπόν ότι εξαιτίας της γραμμικής ταχύτητας των δορυφόρων GPS ο χρόνος καθυστερεί κατά 7.2 μs/ημέρα, ενώ εξαιτίας της απομάκρυνσης των δορυφόρων από τη μάζας της Γης, ο χρόνος επιταχύνεται κατά 45.8 μs/ημέρα (μπλε και πράσινη διακεκομμένες καμπύλες αντίστοιχα, στο παραπάνω διάγραμμα). Συνεπώς υπάρχει συνολικά επιτάχυνση του χρόνου κατά 38.6 μs/ημέρα (κόκκινη καμπύλη), κάτι που διορθώνεται αυτόματα από το σύστημα.
Οι παραπάνω απαιτούμενες διορθώσεις, ήταν μία ακόμα επιβεβαίωση της ακρίβειας της θεωρίας της Σχετικότητας.
Εδώ θα πρέπει να σημειωθεί ότι δεν είναι το τοπικό μηδενικό βαρυτικό πεδίο των δορυφόρων (αποτέλεσμα του ότι βρίσκονται σε τροχιά) που προκαλεί την επιτάχυνση του χρόνου, αλλά η απομάκρυνσή τους από τη μάζα της Γης δηλαδή το ότι κινούνται μέσα σε μειωμένο βαρυτικό πεδίο..
ΥΓ: Το πείραμα των Hafele-Keating το 1971, κατέγραψε την επίδραση της ταχύτητας στην καθυστέρηση του χρόνου (σύμφωνα με την ειδική θεωρία της σχετικότητας), συγκρίνοντας τον χρόνο που έγραψαν δύο εργαστηριακά ατομικά ρολόγια τα οποία τοποθετήθηκαν μέσα σε αντίστοιχα αεροσκάφη που έκαναν τον γύρο του κόσμου, το ένα κινούμενο ανατολικά, ενώ το άλλο δυτικά. Η διαφορά που διαπιστώθηκε σε σχέση με ένα τρίτο όμοιο ατομικό ρολόι στο έδαφος, ήταν -184ns για το πρώτο και +96ns για το δεύτερο. Αυτό οφείλεται στο ότι ενώ τα αεροσκάφη πετούν με σταθερή ταχύτητα ως προς αέρα (άρα και περίπου και ως προς το έδαφος), η ταχύτητά τους προστίθεται ή αφαιρείται ανάλογα, στην επιφανειακή ταχύτητα περιστροφής της Γης και το αποτέλεσμα επηρεάζει τη ροή του χρόνου, η οποία "κυλάει" ως προς ένα σύστημα αναφοράς εκτός Γης (παγκόσμιου χρόνου).
Τελικά, ο Ιούλιος Βερν είχε δίκιο ότι κάνοντας τον γύρω του κόσμου ανατολικά κερδίζεις χρόνο, αλλά όχι μόνον ημερολογιακά αλλά και πραγματικά (αν και βέβαια αυτό το "πραγματικά" είναι ουσιαστικά σε θεωρητικό επίπεδο).
37. Η θεωρία της Σχετικότητας, δύο θεωρίες σε μία.
Μέχρι τώρα έχουμε αναφερθεί αρκετές φορές στη θεωρία της Σχετικότητας.Στην πραγματικότητα όμως πρόκειται για δύο θεωρίες, και οι δύο δημιουργίες του Α. Αϊνστάιν:
-Την Ειδική Σχετικότητα, που παρουσιάστηκε το 1905 και ασχολείται με την επίδραση στην ύλη και στον χρόνο, των ταχυτήτων που πλησιάζουν την ταχύτητα του φωτός (σε μη επιταχυνόμενη κίνηση). Η γνωστή εξίσωση E=mc2, ανήκει σ’ αυτό το τμήμα της θεωρίας.
-Τη Γενική Σχετικότητα, που παρουσιάστηκε το 1915 και ασχολείται με την προέλευση και την επίδραση της βαρύτητας, στην ύλη και στον χρόνο (και σε βαρυτικά επιταχυνόμενη κίνηση).
Το φωτόνιο είναι ένα κβάντο φωτός, δηλαδή το στοιχειώδες (μικρότερο δυνατόν) «πακέτο» φωτεινής ενέργειας.
Όσο για το εάν είναι κύμα ή σωματίδιο, η απάντηση είναι: "και τα δύο!" *, και ανάλογα με τις συνθήκες η συμπεριφορά του φωτονίου ταιριάζει περισσότερο με του ενός ή του άλλου.
Νεότερες απόψεις παρουσιάζουν το φωτόνιο σαν σωματίδιο που περιβάλλεται από ένα κύμα, σαν "φωτοστέφανο".
38. Τελικά τι είναι το φωτόνιο? Και σχετικά με την ταχύτητα του φωτός.
Όσο για το εάν είναι κύμα ή σωματίδιο, η απάντηση είναι: "και τα δύο!" *, και ανάλογα με τις συνθήκες η συμπεριφορά του φωτονίου ταιριάζει περισσότερο με του ενός ή του άλλου.
Νεότερες απόψεις παρουσιάζουν το φωτόνιο σαν σωματίδιο που περιβάλλεται από ένα κύμα, σαν "φωτοστέφανο".
Μία πιο πρακτική προσέγγιση είναι να θεωρήσουμε το φωτόνιο σαν κύμα όσο ταξιδεύει, αλλά σαν σωματίδιο όταν παρατηρείται, όταν δηλαδή αλληλοεπιδρά με έναν ανιχνευτή (φωτόμετρο, μάτι κλπ).
* Ο γνωστός Αμερικανός Φυσικός Ρ. Φέινμαν το διατύπωνε κάπως διαφορετικά: "κανένα από τα δύο!"
* Ο γνωστός Αμερικανός Φυσικός Ρ. Φέινμαν το διατύπωνε κάπως διαφορετικά: "κανένα από τα δύο!"
Σχετικά με την ταχύτητα του φωτός.
Ένα ενδιαφέρον ερώτημα, είναι γιατί η ταχύτητα του φωτός είναι αυτή που είναι.
Κανείς ουσιαστικά δεν ξέρει, και οι προσπάθειες αιώνων επικεντρώνονταν στη μέτρηση της τιμής της με ακρίβεια, καθώς (ειδικά πρόσφατα) η τιμή αυτή υπεισέρχεται σε πλήθος μετρήσεων μεγάλης ακρίβειας που αφορούν συνήθως μεγάλες αποστάσεις (laser, GPS κλπ).
Η (απλοϊκή) άποψη του γράφοντα είναι ότι είναι η μέγιστη δυνατή για "κάτι" χωρίς μάζα, όπως το φωτόνιο, δεν θα μπορούσε όμως να είναι μεγαλύτερη από την ταχύτητα διαστολής του Σύμπαντος σε οποιαδήποτε φάση του, αφού θα έπρεπε να περιέχεται σ' αυτό.
Πάντως πρόκειται για μια σταθερά, που πέρα από την πολύ γνωστή εξίσωση που συσχετίζει μάζα και ενέργεια (βλ εικόνα παραπάνω, καθώς και θέμα Νο 98), συνδέει άμεσα δύο άλλες σταθερές, αυτή της Διηλεκτρικής Σταθεράς του κενού (εο), και της Μαγνητικής Διαπερατότητας του κενού (μο), μέσα από τον τύπο: c2 = 1/e0μ0
39. Γιατί είναι δύσκολο να κατανοήσουμε την Κβαντομηχανική?
Για την ιστορία, η Κβαντομηχανική ξεκίνησε το 1900 με τον Μαξ Πλανκ, αλλά χρειάστηκαν αρκετά χρόνια και η συμβολή αρκετών κορυφαίων Φυσικών (αλλά κυρίως του Μπορ) ώστε να διαμορφωθεί στη σημερινή της μορφή.
Ακόμα όμως και η σημερινή της μορφή μάλλον δεν είναι η τελική, πάντως δίνει συνεπείς απαντήσεις στα παρατηρούμενα περίεργα φαινόμενα σε ατομικό και υποατομικό επίπεδο.
Κατά μία άποψη, το να προσπαθούμε να κατανοήσουμε την Κβαντομηχανική είναι σαν να κοιτάζουμε από πολύ και με το μικροσκόπιο μια φωτογραφία, οπότε διακρίνουμε μόνο τα πίξελ, αλλά μας διαφεύγει η συνολική εικόνα.
Όσο για το ερώτημα γιατί τα φαινόμενα της Κβαντομηχανικής παρατηρούνται μόνο στα πολύ μικρά μεγέθη (συγκεντρώσεις μερικών δεκάδων σωματιδίων ή μεγέθη της τάξης του νανόμετρου), η απάντηση είναι ότι τα φαινόμενα πάντα συμβαίνουν, απλά στα μεγαλύτερα μεγέθη η τυχαιότητα της εμφάνισής τους δεν επηρεάζει τη συνολική εικόνα της "Νευτώνιας" συμπεριφοράς του υλικού.
Λίγα περισσότερα για τη Κβαντομηχανική μπορείτε να διαβάσετε παρακάτω, στο Νο 55.
Η ώσμωση, συνήθως αναφέρεται στα βιβλία της Βιολογίας, πρόκειται όμως για ένα καθαρά φυσικό φαινόμενο, και μάλιστα που φαίνεται να αντιβαίνει στην καθημερινή εμπειρία μας.
Η οποία εμπειρία έχει επηρεαστεί από το γνωστό πείραμα με τα συγκοινωνούντα δοχεία, όπου η ισορροπία μεταξύ των διαφορετικών στηλών του υγρού εξηγείται από το γεγονός ότι προσπαθούν να εξισώσουν τις πιέσεις τους, και ότι εάν μια στήλη περιείχε πυκνότερο υγρό θα χρειαζόταν μικρότερο ύψος για να δημιουργήσει την ίδια πίεση στο κοινό κάτω τμήμα των σωλήνων.
Αυτή η εικόνα ανατρέπεται όμως, αν τα υγρά με διαφορετική πυκνότητα επικοινωνούν μέσω μιας ημιπερατής μεμβράνης.
Εδώ να σημειωθεί όμως, ότι το πυκνότερο υγρό πρέπει να είναι υδατικό διάλυμα βαρύτερων μορίων, όπως το αλάτι πχ, και η μεμβράνη διαπερατή μόνο από μόρια στο μέγεθος του νερού.
Στην περίπτωση αυτή λοιπόν, καθαρό νερό θα περάσει μέσα από την ημιπερατή μεμβράνη προς το διάλυμα (σαν να προσπαθεί να το αραιώσει) και θα αυξήσει τη στάθμη, άρα και την πίεσή του.
Αυτός ο μηχανισμός, που εξηγείται με την κίνηση Brown, υπάρχει στη φύση (ειδικά στα κύτταρα), αλλά αξιοποιείται και στην τεχνολογία αφαλάτωσης, παραγωγής δηλαδή πόσιμου νερού από το θαλασσινό, μέσω του μηχανισμού «αντίστροφης ώσμωσης» όπως ονομάζεται.
Μάλιστα, η νανοτεχνολογία έχει πρόσφατα αναπτύξει μεμβράνες που μπορούν να χρησιμοποιηθούν για αφαλάτωση, με πολύ μικρότερη δαπάνη ενέργειας.
Το ότι το νερό βράζει σε θερμοκρασία περιβάλλοντος αν μειώσουμε αρκετά την ατμοσφαιρική πίεση είναι γνωστό, και συχνά επιδεικνύεται σε σχολικά πειράματα.
Βέβαια το «βράσιμο» αυτό δεν ανεβάζει προφανώς τη θερμοκρασία του νερού, οπότε οι «extreme» ορειβάτες θα έχουν πρόβλημα να φτιάξουν ... καφέ!
Λιγότερο γνωστό όμως είναι ότι μπορούμε να ανάψουμε φωτιά χρησιμοποιώντας κυριολεκτικά «αέρα κοπανιστό», και μια συσκευή που στα αγγλικά ονομάζεται «fire piston» (εικόνα επάνω).
Πρόκειται για μια συσκευή σαν σύριγγα μεσαίου μεγέθους, συνήθως μεταλλική και κλειστή στο ένα της άκρο, που μέσα της εισάγεται μικρή ποσότητα προσανάμματος.
Ένα απότομο και ισχυρό χτύπημα στο έμβολο, αυξάνει στιγμιαία την πίεση του αέρα κατά 25 φορές, οπότε σαν αποτέλεσμα ο αέρας θερμαίνεται (αδιαβατικά) σε πάνω από 200 βαθμούς Κελσίου, και έτσι ανάβει το προσάναμμα.
Αν η μέθοδος σας φαίνεται γνωστή από τον τρόπο που δουλεύουν οι ντίζελ κινητήρες, έχετε απόλυτο δίκαιο!
43. Τριβή και λάστιχα.
Το φαινόμενο του σιφονιού είναι γνωστό, και στηρίζεται στους δεσμούς των μορίων του νερού μεταξύ τους, καθώς και στη διαφορά βαρών των δύο στηλών του νερού που δημιουργούνται.
Λιγότερο γνωστό όμως είναι ότι το ίδιο φαινόμενο μπορεί να αναπαραχθεί με μια αλυσίδα από μικρές μπίλιες που ενώνονται εύκαμπτα μεταξύ τους, όπως πχ οι αλυσιδίτσες που συγκρατούν τις λαστιχένιες τάπες του νεροχύτη.
Το φαινόμενο είναι ιδιαίτερα εντυπωσιακό (ψάξτε στο ίντερνετ: bead chain experiment), καθώς μάλιστα η «ροή» της αλυσίδας υλοποιείται στον αέρα, χωρίς στήριγμα!
Παλαιότερα, πριν από την ανάπτυξη των ηλεκτρικών κινητήρων, ήταν πολύ συνηθισμένη η μεταφορά κίνησης από τον βασικό κινητήρα (συνήθως ατμομηχανή) προς άλλα σημεία, με επίπεδες τροχαλίες και ιμάντες.
Στα παλιά υφαντουργεία και μηχανουργεία μάλιστα, υπήρχε ένα «δάσος» από ιμάντες προς όλες τις κατευθύνσεις που ήταν πολύ επικίνδυνο για τους απρόσεχτους, και ευτυχώς σήμερα έχει εκλείψει.
Οι επίπεδες εκείνες τροχαλίες αντιμετώπιζαν όμως ένα πρόβλημα, που ήταν το να διατηρούν τους (επίσης επίπεδους) ιμάντες κεντραρισμένους, ώστε να μη βγαίνουν κατά τη λειτουργία.
Η λύση μοιάζει «ανάποδη» από αυτό που θα μπορούσε να φανταστεί κανείς και δεν ήταν παρά η κυλινδρική τους επιφάνεια να αποκτήσει ένα ελαφρά «πομπέ» σχήμα, προς τα ΕΞΩ.
Όσο και να φαίνεται περίεργο, με αυτό το ελαφρά βαρελοειδές (μόλις που διακρίνεται με το μάτι) σχήμα της τροχαλίας, αν ο ιμάντας εκτραπεί προς το πλάι, η σφαιρική επιφάνειά οδηγεί τον ιμάντα να κινηθεί πάλι προς το κέντρο της (εικόνα).
Και ΔΕΝ πρέπει να μας παρασύρει η σκέψη ότι το πομπέ της τροχαλίας δημιουργεί μεγαλύτερη τάση στον ιμάντα όταν είναι κεντραρισμένος, άρα το κέντρο της τροχαλίας είναι ένα «ασταθές» σημείο.
48. Το «γαλόνι» της Σιτροέν.
Ίσως έχετε προσέξει ότι οι άξονες μεταφοράς ισχύος τοποθετούνται σε τέτοια σημεία σ’ ένα σύστημα μετάδοσης, ώστε να περιστρέφονται με μεγάλη ταχύτητα.
Αν και αυτό μοιάζει σαν μειονέκτημα, στην πραγματικότητα όσο πιο γρήγορα περιστρέφεται ένας άξονας, τόσο μικρότερη ροπή πρέπει να μεταφέρει για δεδομένη ισχύ, καθώς ισχύει Ρ = Μ x ω.
Η ροπή όμως που μεταφέρεται σχετίζεται με την αντοχή σε στρέψη του άξονα, άρα όσο μεγαλύτερη, τόσο βαρύτερος και ακριβότερος ο άξονας.
Αντίθετα, η μεγάλη ταχύτητα περιστροφής το μόνο που απαιτεί, είναι προσεκτικότερη ζυγοστάθμιση.
Το θέμα αυτό μοιάζει πολύ με το «τρικ» της μεταφοράς σε μεγάλη απόσταση ηλεκτρικής ενέργειας, με μικρές απώλειες.
Θυμίζουμε ότι η ισχύς του ηλεκτρικού ρεύματος είναι P = V x I, ενώ οι απώλειες μεταφοράς (Pμ) είναι ανάλογες με το τετράγωνο της έντασής του Pμ = R x I2
Η εξερεύνηση του Διαστήματος έφτασε σ’ ένα σημείο που έχει φέρει τον άνθρωπο στα όρια της αντοχής του, ως προς τη διάρκεια των μελλοντικών ταξιδιών στο Διάστημα (πχ προς τον Άρη).
Δύο συστήματα όμως μπορούν να προσφέρουν ουσιαστική βοήθεια μελλοντικά:
Ο «πυραυλοκινητήρας» ιόντων και η «πλανητική υποβοήθηση».
Ο κινητήρας ιόντων έχει εξαιρετικά υψηλή ταχύτητα εκτόξευσης των ιόντων, διαδικασία που μπορεί να επιταχύνει ένα ελαφρύ σκάφος σε περισσότερα από 300.000 km/h.
Ο λόγος είναι ότι μέγιστη απόδοση ενός πυραυλοκινητήρα συμβαίνει όταν η ταχύτητα των καυσαερίων (ή ιόντων) είναι περίπου διπλάσια της ταχύτητας του σκάφους, και στους χημικούς πυραύλους η ταχύτητα των καυσαερίων περιορίζεται από την ίδια την ταχύτητα της καύσης.
Αντίθετα, η ταχύτητα των ιόντων (στο κενό) μπορεί να είναι πολύ ψηλότερη, και παρότι ένας κινητήρας ιόντων μπορεί να προσφέρει πολύ ασθενική επιτάχυνση (και μόνο αφού ο διαστημόπλοιο βρεθεί στο Διάστημα), μπορεί να τη διατηρήσει για πολύ μεγάλο χρονικό διάστημα, και μάλιστα με μικρή κατανάλωση καυσίμου.
Το δεύτερο σύστημα είναι η πλανητική υποβοήθηση, που βασίζεται στο ότι αν ένα διαστημόπλοιο πλησιάσει «μετωπικά» έναν πλανήτη με μικρή γωνία ως προς την κατεύθυνση κίνησής του, μπει σε τροχιά γύρω του για μισή περίπου περιστροφή και εκτοξευτεί σχετικά αντίθετα από την κατεύθυνση από την οποία ήλθε, μπορεί να προσθέσει στην αρχική ταχύτητά του, μέχρι και δύο φορές τη γραμμική ταχύτητα του πλανήτη. Στην πράξη βέβαια, η αλλαγή πορείας του διαστημοπλοίου δεν είναι τόσο ακραία, αλλά τόση όση χρειάζεται για το επιθυμητό αποτέλεσμα. Με αντίστοιχο τρόπο, μπορεί να γίνει και "φρενάρισμα" των διαστημοπλοίων προκειμένου να μπουν σε τροχιά γύρω από τους εσωτερικούς (ως προς τη Γη) πλανήτες του Ηλιακού Συστήματος.
51. Το «αλλόκοτο» φαινόμενο Mpemba.
Απ’ όλα τα περίεργα φαινόμενα της θερμοδυναμικής, το φαινόμενο Mpemba, διεκδικεί μάλλον τα πρωτεία. Ο Mpemba ήταν μαθητής γυμνασίου στην Τασμανία το 1969, όταν παρατήρησε ότι δοχεία με παγωτό αρχικά, και νερό αργότερα, έπηζαν το περιεχόμενό τους ταχύτερα όταν τοποθετούνταν στο ψυγείο έχοντας υψηλότερη αρχική θερμοκρασία.
Αφού υπέμενε για μερικά χρόνια τη σχετική «καζούρα», τελικά η επιμονή του νίκησε και η επιστημονική κοινότητα επιβεβαίωσε το φαινόμενο, δίνοντάς του μάλιστα το όνομα του παρατηρητικού μαθητή.
Ακόμα πιο περίεργο είναι ότι γεγονός ότι το φαινόμενο αυτό ήταν γνωστό από την εποχή του Αριστοτέλη, αλλά αγνοήθηκε από τους μεταγενέστερους, μάλλον επειδή δεν μπορούσαν να το εξηγήσουν!
Βέβαια το φαινόμενο δεν παρατηρείται πάντοτε, χωρίς να έχουν προσδιοριστεί ακριβώς ούτε οι συνθήκες στις οποίες συμβαίνει ούτε να έχει δοθεί τελείως ικανοποιητική εξήγηση γιατί συμβαίνει.
Η καλύτερη εξήγηση πάντως είναι ότι προκαλείται από τα διαλυμένα αέρια στο νερό, που επειδή διαφεύγουν ευκολότερα στις υψηλότερες θερμοκρασίες, καθιστούν το θερμό νερό πιο ομοιογενές ή "συμπαγές", επιτρέποντας τη γρηγορότερη ψύξη του. Σ’ αυτό συνηγορεί και το γεγονός ότι το φαινόμενο γίνεται τόσο πιο έντονο, όσο περισσότερο αέριο περιέχει αρχικά το νερό.
Κάτι αντίστοιχο συμβαίνει και όταν το νερό είναι πολύ καθαρό ή απεσταγμένο*, οπότε μπορεί να παραμείνει υγρό σε χαμηλότερη θερμοκρασία από τους 0ο Kελσίου, και να παγώσει απότομα από μια διαταραχή (κούνημα του δοχείου, πρόσκρουση «υπέρψυχρων» σταγόνων σε επιφάνεια κλπ).
*Το συνηθισμένο νερό περιέχει αρκετή ποσότητα αερίων, που δίνουν «γαλακτερή» όψη στον πάγο. Νερό απαλλαγμένο από αέρια (πχ με προηγούμενη θέρμανση), δίνει τελείως διάφανο πάγο.
Πετάει!, αν και το ακριβέστερο είναι ότι αιωρείται, αρκεί το μαγνητικό πεδίο να είναι αρκετά ισχυρό (τουλάχιστον 15 Τ, που είναι ΠΟΛΥ ισχυρό * και δημιουργείται με ειδικά δισκοειδή πηνία, που ονομάζεται πηνία Bitter).
Στις συνθήκες αυτές, ακόμα και τα μη μαγνητικά (διαμαγνητικά) υλικά όπως το νερό αντιδρούν στο μαγνητικό πεδίο και μάλιστα με τρόπο ώστε να απωθούνται απ' αυτό **, οπότε ακόμα και ένας ζωντανός βάτραχος μπορεί να αιωρηθεί χωρίς δυσμενείς επιπτώσεις για την υγεία του.
* Για σύγκριση, ο ισχυρότερος μόνιμος μαγνήτης δεν ξεπερνά το 1.5 Τ, τα μαγνητικά πεδία των ηλεκτρομαγνητών στο CERN δεν ξεπερνούν τα 10 T, ενώ το ισχυρότερο μαγνητικό πεδίο που έχει δημιουργηθεί (από πηνία Bitter) είναι 45 Τ.
** Αντίθετα, τα υλικά από σίδηρο (σιδηρομαγνητικά) αλλά και τα λιγότερο μαγνητικά (παραμαγνητικά), αντιδρούν με τρόπο ώστε να έλκονται από το μαγνητικό πεδίο.
53. Η Φύση αγαπάει την "αταξία"!
Και την αγαπάει πράγματι, επειδή είναι μια πιο «οικονομική» ή σταθερή κατάσταση από πλευράς ενέργειας όσον αφορά στη διάταξη των μορίων, με περίπου αντίστοιχο τρόπο που η ευσταθής ισορροπία είναι από πλευράς μηχανικής ενέργειας οικονομικότερη κατάσταση σε σχέση με την ασταθή ισορροπία.
Όπως λοιπόν, εάν μια εδαφική περιοχή αφεθεί μόνο στις δυνάμεις της διάβρωσης θα καταλήξει επίπεδη μετά από ΠΟΛΥ χρόνο, έτσι και ενεργειακά ένα σύστημα θα καταλήξει μακροχρόνια σε πλήρη «αταξία», καθώς όλο και μεγαλύτερο μέρος της ενέργειάς του θα υποβαθμίζεται σε θερμότητα, δηλαδή σε άτακτη κίνηση των μορίων του.
Μέτρο αυτής της αταξίας είναι η ελληνική λέξη Εντροπία (από το εν + τροπή) που χρησιμοποιείται διεθνώς και συνιστά μία από τις σημαντικότερες λέξεις της Θερμοδυναμικής.
Ένα απλό παράδειγμα είναι μια τάξη με ζωηρούς μαθητές.
Χρειάζεται προσπάθεια (έργο) από την πλευρά του δάσκαλου για να βάλει (ή να επαναφέρει) τους μαθητές σε τάξη, αλλά στην πρώτη ευκαιρία οι μαθητές του θα επιβεβαιώσουν περίτρανα την τάση ενός συστήματος να ρέπει προς την αύξηση της Εντροπίας του.
Μια δεύτερη σημαντική ελληνική (και επίσης διεθνής) λέξη στον τομέα της Θερμοδυναμικής είναι και η Ενθαλπία (εν + θάλπω*), που είναι το μέτρο της περιεχόμενης θερμικής ενέργειας ενός συστήματος.
Υπόψη ότι και οι δύο αυτές ελληνικές λέξεις έχουν καθιερωθεί από ξένους επιστήμονες (Clausius και Onnes αντίστοιχα).
* σύγκρινε και το: περι + θάλπω
Λίγα περισσότερα για τη Κβαντομηχανική μπορείτε να διαβάσετε παρακάτω, στο Νο 55.
40. Η πυρηνική ενέργεια. Τόσο απλή, τόσο πολύπλοκη!
Η πυρηνική ενέργεια που κάποτε φαινόταν σαν "Η" λύση στα προβλήματα ενέργειας της ανθρωπότητας, σήμερα είναι σε «δυσμένεια».
Θεωρώντας ότι τα βασικά για την πυρηνική ενέργεια είναι γνωστά, θα εστιάσουμε στα δύο είδη της πυρηνικής ενέργειας, τη Σχάση και τη Σύντηξη.
Η σχάση είναι «σχετικά» εύκολη, το δυσκολότερο τμήμα της είναι η απομόνωση του κατάλληλου ισότοπου ουρανίου, από το αρχικό ορυκτό που το περιέχει σε πολύ μικρές ποσότητες.
Η ενέργεια σχάσης αξιοποιείται πάντοτε σαν θερμική ενέργεια.
Ο «πυρήνας» θερμαίνεται από τις ραδιενεργές διασπάσεις και η θερμότητα αυτή χρησιμοποιείται για την παραγωγή ατμού, όπως χρησιμοποιείται το καύσιμο στον λέβητα σε οποιοδήποτε θερμικό εργοστάσιο παραγωγής ηλεκτρικής ενέργειας.
Ακόμα και οι πυρηνικές κυψέλες που τοποθετούνται στα διαστημόπλοια για την απ’ ευθείας παραγωγή ρεύματος, έχουν σαν ρόλο να θερμαίνουν ένα διμεταλλικό κύκλωμα στο οποίο η διαφορά θερμοκρασίας με το άλλο άκρο του παράγει ηλεκτρισμό.
Βέβαια, η σχάση έχει σαν υποπροϊόντα ραδιενεργά υλικά και ακτινοβολία, και η μέχρι τώρα εμπειρία έχει δείξει ότι καμία κατασκευή δεν μπορεί να θεωρηθεί απολύτως «απρόσβλητη» από ανθρώπινο λάθος ή φυσική καταστροφή.
Φυσικά, η διαρροή ραδιενέργειας δεν είναι καθόλου αποτρεπτική ώστε τη σχάση να χρησιμοποιηθεί για την κατασκευή βόμβας!
Από την άλλη πλευρά, η σύντηξη μοιάζει να έχει όλα τα πλεονεκτήματα, αλλά και ένα μεγάλο μειονέκτημα!
Για να ξεκινήσει χρειάζεται να έχει δημιουργηθεί περιβάλλον πολύ υψηλής πίεσης και θερμοκρασίας*, κάτι εύκολο όταν πρόκειται για βόμβα, καθώς η βόμβα σύντηξης περιλαμβάνει και μια βόμβα σχάσης σε ρόλο «πυροκροτητή».
Αντίθετα όμως, για ειρηνική χρήση η σύντηξη προϋποθέτει τη δημιουργία πολύ ισχυρών μαγνητικών πεδίων, και τη χρήση ακόμα πιο ισχυρών laser που θα στοχεύσουν (μέσα σε θάλαμο απόλυτου κενού) μια μικροσκοπική μπίλια από υλικό που έχει προσροφήσει υδρογόνο ή κάποια από τα ισότοπά του, ώστε να πυροδοτηθεί η σύντηξη.
Αλλά και τότε το «καύσιμο» θα πρέπει να ανανεώνεται περιοδικά, και το απόλυτο κενό που το περιβάλλει δεν βοηθάει καθόλου τη μετάδοση της θερμότητας προς τα έξω για αξιοποίηση.
Επιπλέον, η ενέργεια που χρειάζονται οι μαγνήτες και τα laser, ισοσκελίζουν (τουλάχιστον προς το παρόν) την όποια ενέργεια παράγεται.
Έτσι λοιπόν, ενώ η πρώτη βόμβα σχάσης δοκιμάστηκε το 1945 (ΗΠΑ) και η πρώτη βόμβα υδρογόνου δοκιμάστηκε το 1952 (ΗΠΑ), το πρώτο εργοστάσιο ηλεκτροπαραγωγής με πυρηνική ενέργεια λειτούργησε το 1954 (σημερινή Ρωσία), αλλά το πρώτο εργοστάσιο σύντηξης δεν φαίνεται ακόμα ούτε στον ορίζοντα!
Στο μεταξύ υπάρχουν ισχυρισμοί και ελπίδες για την κατασκευή συστημάτων «ψυχρής σύντηξης», που δεν θα απαιτούν δηλαδή τις κλασικές συνθήκες πολύ υψηλής πίεσης και θερμοκρασίας, αλλά τίποτα δεν έχει επιβεβαιωθεί ακόμα (βλ και: https://geometax12.blogspot.com/2023/01/blog-post.html) .
*Οι ίδιες συνθήκες επικρατούν στον Ήλιο, που αποτελείται κυρίως από υδρογόνο και (το παράγωγο της σύντηξης) ήλιο. Η τεράστια πίεση δημιουργείται από την ίδια τη βαρύτητα του Ήλιου εξαιτίας της τεράστιας μάζας του, ενώ η θερμοκρασία είναι αποτέλεσμα της πίεσης αυτής. Η (προς τα έξω) πίεση από τη σύντηξη ισορροπεί με την (προς τα μέσα) πίεση από τη βαρύτητα του Ήλιου.
ΥΓ. Μετά τα προβλήματα της ενεργειακής επάρκειας στην Ευρώπη το 2022, η πυρηνική ενέργεια δεν μοιάζει πλέον τόσο μεγάλος "μπαμπούλας", και όλο και περισσότερο γίνεται κουβέντα για τα πλεονεκτήματά της. ίσως στο κοντινό μέλλον η λύση των αλάτων θορίου δώσει μια παράταση ζωής στη "γηραιά" τεχνολογία της σχάσης.
41. Ώσμωση, ένα περίεργο φαινόμενο.
Η οποία εμπειρία έχει επηρεαστεί από το γνωστό πείραμα με τα συγκοινωνούντα δοχεία, όπου η ισορροπία μεταξύ των διαφορετικών στηλών του υγρού εξηγείται από το γεγονός ότι προσπαθούν να εξισώσουν τις πιέσεις τους, και ότι εάν μια στήλη περιείχε πυκνότερο υγρό θα χρειαζόταν μικρότερο ύψος για να δημιουργήσει την ίδια πίεση στο κοινό κάτω τμήμα των σωλήνων.
Αυτή η εικόνα ανατρέπεται όμως, αν τα υγρά με διαφορετική πυκνότητα επικοινωνούν μέσω μιας ημιπερατής μεμβράνης.
Εδώ να σημειωθεί όμως, ότι το πυκνότερο υγρό πρέπει να είναι υδατικό διάλυμα βαρύτερων μορίων, όπως το αλάτι πχ, και η μεμβράνη διαπερατή μόνο από μόρια στο μέγεθος του νερού.
Στην περίπτωση αυτή λοιπόν, καθαρό νερό θα περάσει μέσα από την ημιπερατή μεμβράνη προς το διάλυμα (σαν να προσπαθεί να το αραιώσει) και θα αυξήσει τη στάθμη, άρα και την πίεσή του.
Αυτός ο μηχανισμός, που εξηγείται με την κίνηση Brown, υπάρχει στη φύση (ειδικά στα κύτταρα), αλλά αξιοποιείται και στην τεχνολογία αφαλάτωσης, παραγωγής δηλαδή πόσιμου νερού από το θαλασσινό, μέσω του μηχανισμού «αντίστροφης ώσμωσης» όπως ονομάζεται.
Μάλιστα, η νανοτεχνολογία έχει πρόσφατα αναπτύξει μεμβράνες που μπορούν να χρησιμοποιηθούν για αφαλάτωση, με πολύ μικρότερη δαπάνη ενέργειας.
Τελικά, μπορούμε να θεωρήσουμε την ώσμωση σαν μια έκφραση της τάσης της Φύσης προς ομοιομορφία και σταθερότητα.
42. Βράσιμο χωρίς, και άναμμα φωτιάς με, ... αέρα.
Βέβαια το «βράσιμο» αυτό δεν ανεβάζει προφανώς τη θερμοκρασία του νερού, οπότε οι «extreme» ορειβάτες θα έχουν πρόβλημα να φτιάξουν ... καφέ!
Λιγότερο γνωστό όμως είναι ότι μπορούμε να ανάψουμε φωτιά χρησιμοποιώντας κυριολεκτικά «αέρα κοπανιστό», και μια συσκευή που στα αγγλικά ονομάζεται «fire piston» (εικόνα επάνω).
Πρόκειται για μια συσκευή σαν σύριγγα μεσαίου μεγέθους, συνήθως μεταλλική και κλειστή στο ένα της άκρο, που μέσα της εισάγεται μικρή ποσότητα προσανάμματος.
Ένα απότομο και ισχυρό χτύπημα στο έμβολο, αυξάνει στιγμιαία την πίεση του αέρα κατά 25 φορές, οπότε σαν αποτέλεσμα ο αέρας θερμαίνεται (αδιαβατικά) σε πάνω από 200 βαθμούς Κελσίου, και έτσι ανάβει το προσάναμμα.
Αν η μέθοδος σας φαίνεται γνωστή από τον τρόπο που δουλεύουν οι ντίζελ κινητήρες, έχετε απόλυτο δίκαιο!
43. Τριβή και λάστιχα.
Στο σχολείο μαθαίνουμε ότι η τριβή είναι ανεξάρτητη από την επιφάνεια επαφής.
Γιατί τότε στα σπορ αυτοκίνητα τα λάστιχα είναι πολύ φαρδύτερα από τα συνηθισμένα?
Γιατί ενώ η τριβή είναι πράγματι ανεξάρτητη από την επιφάνεια επαφής, ένα στενό λάστιχο παραμορφώνεται εύκολα, με συνέπεια να μειώνεται ουσιαστικά η επιφάνεια επαφής του με τον δρόμο, οπότε αν πρέπει να μεταφέρει και σημαντική ισχύ υπερθερμαίνεται και λιώνει τοπικά, και τότε ο συντελεστής τριβής πάει ... περίπατο.
Το ίδιο συμβαίνει αν σε ισχυρό φρενάρισμα ένας τροχός «μπλοκάρει», οπότε πάλι το λάστιχο λιώνει στην επιφάνεια επαφής του με την άσφαλτο, και η τριβή μειώνεται σημαντικά.
44. Η πίεση των υγρών.
Η πίεση των υγρών που έχουν ελεύθερη επιφάνεια, προκαλείται από τη βαρύτητα.
Γι’ αυτό υγρά σε τροχιά (σε μικροβαρύτητα) δεν δημιουργούν πίεση οσοδήποτε και να είναι το ύψος του δοχείου που τα περιέχει, και μάλιστα το νερό πχ μπορεί να βγει από το δοχείο του και να αιωρείται.
Παρούσες είναι μόνο οι ελάχιστες δυνάμεις της επιφανειακής τάσης του νερού, που τείνουν να του δώσουν σφαιρικό σχήμα.
Αντίθετα, η δημιουργία ισχυρού βαρυτικού πεδίου με φυγοκέντρηση χρησιμοποιείται για την επιτάχυνση του διαχωρισμού υγρών που δεν αναμιγνύονται, όπως νερό και λάδι, ή το γρήγορο κατακάθισμα στερεών συστατικών σε υγρό, όπως σε δείγματα αίματος. Στην εικόνα, η φυσαλίδα στην μπάλα νερού σε συνθήκες μικροβαρύτητας, δεν έχει την τάση να μετακινηθεί.
45. Γιατί όλες οι παλίρροιες δεν είναι ίσες.
Εννοούμε φυσικά τις παλίρροιες στην ίδια περιοχή της Γης.
Κατ’ αρχήν οι παλίρροιες συμβαίνουν με τη διπλάσια συχνότητα απ’ ότι θα περίμενε κανείς, αφού οφείλονται βασικά στη έλξη της Σελήνης, η οποία μεσουρανεί σε κάθε τόπο κάθε 25 περίπου ώρες.
Όμως, ενώ είναι εύκολο να καταλάβουμε ότι η Σελήνη έλκει το νερό που βρίσκεται "απέναντί" της, χρειάζεται λίγη φαντασία για να συνειδητοποιήσουμε ότι εξαιτίας της μεγαλύτερης απόστασης, ασκεί ταυτόχρονα μειωμένη έλξη στο νερό που βρίσκεται αντιδιαμετρικά στη Γη, σε σχέση με το νερό που βρίσκεται κάθετα στον άξονα Γης - Σελήνης (υπόψην ότι Γη και Σελήνη περιφέρονται περίπου στο ίδιο επίπεδο σε σχέση με τον Ήλιο).
Κατά συνέπεια, το νερό από την περιοχή των πόλων έχει την τάση να μετακινηθεί και να «φουσκώσει» και στην αντίθετη πλευρά από αυτή που βρίσκεται η Σελήνη.
Έτσι καταλήγει ο κύκλος της παλίρροιας να συμβαίνει δύο φορές το 25-ωρο (καθώς εξαρτάται κυρίως από τη Σελήνη), αν και προφανώς όχι με την ίδια ένταση.
Επιπλέον, η ένταση των παλιρροιών επηρεάζεται και από τη θέση του Ήλιου, καθώς η έλξη του (περίπου η μισή από αυτή της Σελήνης) μπορεί να ενισχύει ή να μειώνει αυτήν της Σελήνης.
Μάλιστα, αν στη σύμπτωση να βρεθούν από την ίδια πλευρά ή αντιδιαμετρικά (ως προς τη Γη) ο Ήλιος και η Σελήνη (όταν δηλαδή είναι Νέα Σελήνη ή Πανσέληνος), προστεθεί και η σύμπτωση μιας σημαντικής μεταβολή του βαρομετρικού, όπως υψηλό βαρομετρικό στις περιοχές που βρίσκονται σε άμπωτη, τότε η στάθμη της θάλασσας μπορεί να κατέβει σημαντικά (το αντίθετο φυσικά συμβαίνει, σε σύμπτωση χαμηλού βαρομετρικού με πλημμυρίδα). Ακόμα πιο έντονη μπορεί να γίνει η άμπωτη, όταν για αρκετό διάστημα πνέει ισχυρός άνεμος από την ξηρά προς τη θάλασσα. Κάτι τέτοιο συνέβη στην Ελλάδα στις αρχές του Μαρτίου του 2021, παρότι η άμπωτη που οφείλεται στα αστρονομικά φαινόμενα, δεν ήταν από τις ισχυρότερες εκείνες τις ημέρες.
Γιατί τότε στα σπορ αυτοκίνητα τα λάστιχα είναι πολύ φαρδύτερα από τα συνηθισμένα?
Γιατί ενώ η τριβή είναι πράγματι ανεξάρτητη από την επιφάνεια επαφής, ένα στενό λάστιχο παραμορφώνεται εύκολα, με συνέπεια να μειώνεται ουσιαστικά η επιφάνεια επαφής του με τον δρόμο, οπότε αν πρέπει να μεταφέρει και σημαντική ισχύ υπερθερμαίνεται και λιώνει τοπικά, και τότε ο συντελεστής τριβής πάει ... περίπατο.
Το ίδιο συμβαίνει αν σε ισχυρό φρενάρισμα ένας τροχός «μπλοκάρει», οπότε πάλι το λάστιχο λιώνει στην επιφάνεια επαφής του με την άσφαλτο, και η τριβή μειώνεται σημαντικά.
44. Η πίεση των υγρών.
Γι’ αυτό υγρά σε τροχιά (σε μικροβαρύτητα) δεν δημιουργούν πίεση οσοδήποτε και να είναι το ύψος του δοχείου που τα περιέχει, και μάλιστα το νερό πχ μπορεί να βγει από το δοχείο του και να αιωρείται.
Παρούσες είναι μόνο οι ελάχιστες δυνάμεις της επιφανειακής τάσης του νερού, που τείνουν να του δώσουν σφαιρικό σχήμα.
Αντίθετα, η δημιουργία ισχυρού βαρυτικού πεδίου με φυγοκέντρηση χρησιμοποιείται για την επιτάχυνση του διαχωρισμού υγρών που δεν αναμιγνύονται, όπως νερό και λάδι, ή το γρήγορο κατακάθισμα στερεών συστατικών σε υγρό, όπως σε δείγματα αίματος. Στην εικόνα, η φυσαλίδα στην μπάλα νερού σε συνθήκες μικροβαρύτητας, δεν έχει την τάση να μετακινηθεί.
45. Γιατί όλες οι παλίρροιες δεν είναι ίσες.
Κατ’ αρχήν οι παλίρροιες συμβαίνουν με τη διπλάσια συχνότητα απ’ ότι θα περίμενε κανείς, αφού οφείλονται βασικά στη έλξη της Σελήνης, η οποία μεσουρανεί σε κάθε τόπο κάθε 25 περίπου ώρες.
Όμως, ενώ είναι εύκολο να καταλάβουμε ότι η Σελήνη έλκει το νερό που βρίσκεται "απέναντί" της, χρειάζεται λίγη φαντασία για να συνειδητοποιήσουμε ότι εξαιτίας της μεγαλύτερης απόστασης, ασκεί ταυτόχρονα μειωμένη έλξη στο νερό που βρίσκεται αντιδιαμετρικά στη Γη, σε σχέση με το νερό που βρίσκεται κάθετα στον άξονα Γης - Σελήνης (υπόψην ότι Γη και Σελήνη περιφέρονται περίπου στο ίδιο επίπεδο σε σχέση με τον Ήλιο).
Κατά συνέπεια, το νερό από την περιοχή των πόλων έχει την τάση να μετακινηθεί και να «φουσκώσει» και στην αντίθετη πλευρά από αυτή που βρίσκεται η Σελήνη.
Έτσι καταλήγει ο κύκλος της παλίρροιας να συμβαίνει δύο φορές το 25-ωρο (καθώς εξαρτάται κυρίως από τη Σελήνη), αν και προφανώς όχι με την ίδια ένταση.
Επιπλέον, η ένταση των παλιρροιών επηρεάζεται και από τη θέση του Ήλιου, καθώς η έλξη του (περίπου η μισή από αυτή της Σελήνης) μπορεί να ενισχύει ή να μειώνει αυτήν της Σελήνης.
Μάλιστα, αν στη σύμπτωση να βρεθούν από την ίδια πλευρά ή αντιδιαμετρικά (ως προς τη Γη) ο Ήλιος και η Σελήνη (όταν δηλαδή είναι Νέα Σελήνη ή Πανσέληνος), προστεθεί και η σύμπτωση μιας σημαντικής μεταβολή του βαρομετρικού, όπως υψηλό βαρομετρικό στις περιοχές που βρίσκονται σε άμπωτη, τότε η στάθμη της θάλασσας μπορεί να κατέβει σημαντικά (το αντίθετο φυσικά συμβαίνει, σε σύμπτωση χαμηλού βαρομετρικού με πλημμυρίδα). Ακόμα πιο έντονη μπορεί να γίνει η άμπωτη, όταν για αρκετό διάστημα πνέει ισχυρός άνεμος από την ξηρά προς τη θάλασσα. Κάτι τέτοιο συνέβη στην Ελλάδα στις αρχές του Μαρτίου του 2021, παρότι η άμπωτη που οφείλεται στα αστρονομικά φαινόμενα, δεν ήταν από τις ισχυρότερες εκείνες τις ημέρες.
ΥΓ. Ακόμα και το σχήμα όλης της Γης επηρεάζεται από τις παλιρροϊκές δυνάμεις, με το έδαφος να μεταβάλει το ύψος του μέχρι και 30cm, ανεξάρτητα από την παρουσία νερού ή όχι.
46. Ένα σιφόνι από μπίλιες.
Λιγότερο γνωστό όμως είναι ότι το ίδιο φαινόμενο μπορεί να αναπαραχθεί με μια αλυσίδα από μικρές μπίλιες που ενώνονται εύκαμπτα μεταξύ τους, όπως πχ οι αλυσιδίτσες που συγκρατούν τις λαστιχένιες τάπες του νεροχύτη.
Το φαινόμενο είναι ιδιαίτερα εντυπωσιακό (ψάξτε στο ίντερνετ: bead chain experiment), καθώς μάλιστα η «ροή» της αλυσίδας υλοποιείται στον αέρα, χωρίς στήριγμα!
47. Η επίπεδη τροχαλία που δεν είναι ... επίπεδη.
Παλαιότερα, πριν από την ανάπτυξη των ηλεκτρικών κινητήρων, ήταν πολύ συνηθισμένη η μεταφορά κίνησης από τον βασικό κινητήρα (συνήθως ατμομηχανή) προς άλλα σημεία, με επίπεδες τροχαλίες και ιμάντες.
Στα παλιά υφαντουργεία και μηχανουργεία μάλιστα, υπήρχε ένα «δάσος» από ιμάντες προς όλες τις κατευθύνσεις που ήταν πολύ επικίνδυνο για τους απρόσεχτους, και ευτυχώς σήμερα έχει εκλείψει.
Οι επίπεδες εκείνες τροχαλίες αντιμετώπιζαν όμως ένα πρόβλημα, που ήταν το να διατηρούν τους (επίσης επίπεδους) ιμάντες κεντραρισμένους, ώστε να μη βγαίνουν κατά τη λειτουργία.
Η λύση μοιάζει «ανάποδη» από αυτό που θα μπορούσε να φανταστεί κανείς και δεν ήταν παρά η κυλινδρική τους επιφάνεια να αποκτήσει ένα ελαφρά «πομπέ» σχήμα, προς τα ΕΞΩ.
Όσο και να φαίνεται περίεργο, με αυτό το ελαφρά βαρελοειδές (μόλις που διακρίνεται με το μάτι) σχήμα της τροχαλίας, αν ο ιμάντας εκτραπεί προς το πλάι, η σφαιρική επιφάνειά οδηγεί τον ιμάντα να κινηθεί πάλι προς το κέντρο της (εικόνα).
Και ΔΕΝ πρέπει να μας παρασύρει η σκέψη ότι το πομπέ της τροχαλίας δημιουργεί μεγαλύτερη τάση στον ιμάντα όταν είναι κεντραρισμένος, άρα το κέντρο της τροχαλίας είναι ένα «ασταθές» σημείο.
48. Το «γαλόνι» της Σιτροέν.
Το γνωστό σήμα των αυτοκινήτων Σιτροέν θυμίζει το γαλόνι λοχία, ανεστραμμένο.
Δεν σχετίζεται όμως με τον στρατό, αλλά με μια εφεύρεση του ίδιου του Σιτροέν στις αρχές του 20ου αιώνα, για τα διπλά λοξά γρανάζια.
Αρχικά, τα γρανάζια είχαν ευθύγραμμα δόντια, παράλληλα με τον άξονά τους.
Τα γρανάζια αυτά ήταν εύκολα στην κατασκευή, αλλά επίσης θορυβώδη και εμπλέκανε ένα ζευγάρι δόντια κάθε φορά.
Έτσι άρχισαν να κατασκευάζονται γρανάζια με λοξά δόντια, που έλυσαν τα προηγούμενα προβλήματα, αλλά καθώς οι ροπές που έπρεπε να μεταφερθούν αυξάνονταν με την πρόοδο της τεχνολογίας, προέκυψε ένα άλλο πρόβλημα.
Τα λοξά δόντια προκαλούσαν ωστικές δυνάμεις, δηλαδή διαμήκεις δυνάμεις στον άξονά τους, που δημιουργούσαν σημαντικά προβλήματα φθοράς στα ρουλεμάν και λοιπά έδρανα της εποχής εκείνης.
Ο Σιτροέν έλυσε με απλό και ευφυή τρόπο το πρόβλημα αυτό, κατασκευάζοντας γρανάζια με διπλά αντίθετης κλίσης λοξά δόντια, που αλληλοαναιρούσαν τις ωστικές δυνάμεις.
Το σύστημα αυτό ήταν τόσο πετυχημένο που ο Σιτροέν το επέλεξε σαν σήμα των αυτοκινήτων που δημιούργησε στη συνέχεια.
49. Άξονες και ροπή, καλώδια και ένταση (βλ και θέμα 104).
Δεν σχετίζεται όμως με τον στρατό, αλλά με μια εφεύρεση του ίδιου του Σιτροέν στις αρχές του 20ου αιώνα, για τα διπλά λοξά γρανάζια.
Αρχικά, τα γρανάζια είχαν ευθύγραμμα δόντια, παράλληλα με τον άξονά τους.
Τα γρανάζια αυτά ήταν εύκολα στην κατασκευή, αλλά επίσης θορυβώδη και εμπλέκανε ένα ζευγάρι δόντια κάθε φορά.
Έτσι άρχισαν να κατασκευάζονται γρανάζια με λοξά δόντια, που έλυσαν τα προηγούμενα προβλήματα, αλλά καθώς οι ροπές που έπρεπε να μεταφερθούν αυξάνονταν με την πρόοδο της τεχνολογίας, προέκυψε ένα άλλο πρόβλημα.
Τα λοξά δόντια προκαλούσαν ωστικές δυνάμεις, δηλαδή διαμήκεις δυνάμεις στον άξονά τους, που δημιουργούσαν σημαντικά προβλήματα φθοράς στα ρουλεμάν και λοιπά έδρανα της εποχής εκείνης.
Ο Σιτροέν έλυσε με απλό και ευφυή τρόπο το πρόβλημα αυτό, κατασκευάζοντας γρανάζια με διπλά αντίθετης κλίσης λοξά δόντια, που αλληλοαναιρούσαν τις ωστικές δυνάμεις.
Το σύστημα αυτό ήταν τόσο πετυχημένο που ο Σιτροέν το επέλεξε σαν σήμα των αυτοκινήτων που δημιούργησε στη συνέχεια.
49. Άξονες και ροπή, καλώδια και ένταση (βλ και θέμα 104).
Οπτικοποίηση του αποτελέσματος υπερβολικής ροπής για τον συγκεκριμένο άξονα.
Αν και αυτό μοιάζει σαν μειονέκτημα, στην πραγματικότητα όσο πιο γρήγορα περιστρέφεται ένας άξονας, τόσο μικρότερη ροπή πρέπει να μεταφέρει για δεδομένη ισχύ, καθώς ισχύει Ρ = Μ x ω.
Η ροπή όμως που μεταφέρεται σχετίζεται με την αντοχή σε στρέψη του άξονα, άρα όσο μεγαλύτερη, τόσο βαρύτερος και ακριβότερος ο άξονας.
Αντίθετα, η μεγάλη ταχύτητα περιστροφής το μόνο που απαιτεί, είναι προσεκτικότερη ζυγοστάθμιση.
Το θέμα αυτό μοιάζει πολύ με το «τρικ» της μεταφοράς σε μεγάλη απόσταση ηλεκτρικής ενέργειας, με μικρές απώλειες.
Θυμίζουμε ότι η ισχύς του ηλεκτρικού ρεύματος είναι P = V x I, ενώ οι απώλειες μεταφοράς (Pμ) είναι ανάλογες με το τετράγωνο της έντασής του Pμ = R x I2
Χρησιμοποιώντας λοιπόν τη δυνατότητα του εναλλασσόμενου ρεύματος να μετασχηματίζεται αυξάνουμε την τάση του, οπότε (για δεδομένη ισχύ) μειώνεται η έντασή του, και κάνουμε τη δουλειά μας πολύ πιο οικονομικά (μικρότερες απώλειες και λεπτότεροι αγωγοί).
Ενώ η μόνη επίπτωση από την υψηλότερη τάση, είναι μεγαλύτερες αποστάσεις ασφαλείας και παχύτερη μόνωση.
Ενώ η μόνη επίπτωση από την υψηλότερη τάση, είναι μεγαλύτερες αποστάσεις ασφαλείας και παχύτερη μόνωση.
50. Πώς θα καλύψουμε τις μεγάλες αποστάσεις στο Διάστημα.
Δύο συστήματα όμως μπορούν να προσφέρουν ουσιαστική βοήθεια μελλοντικά:
Ο «πυραυλοκινητήρας» ιόντων και η «πλανητική υποβοήθηση».
Ο κινητήρας ιόντων έχει εξαιρετικά υψηλή ταχύτητα εκτόξευσης των ιόντων, διαδικασία που μπορεί να επιταχύνει ένα ελαφρύ σκάφος σε περισσότερα από 300.000 km/h.
Ο λόγος είναι ότι μέγιστη απόδοση ενός πυραυλοκινητήρα συμβαίνει όταν η ταχύτητα των καυσαερίων (ή ιόντων) είναι περίπου διπλάσια της ταχύτητας του σκάφους, και στους χημικούς πυραύλους η ταχύτητα των καυσαερίων περιορίζεται από την ίδια την ταχύτητα της καύσης.
Αντίθετα, η ταχύτητα των ιόντων (στο κενό) μπορεί να είναι πολύ ψηλότερη, και παρότι ένας κινητήρας ιόντων μπορεί να προσφέρει πολύ ασθενική επιτάχυνση (και μόνο αφού ο διαστημόπλοιο βρεθεί στο Διάστημα), μπορεί να τη διατηρήσει για πολύ μεγάλο χρονικό διάστημα, και μάλιστα με μικρή κατανάλωση καυσίμου.
Το δεύτερο σύστημα είναι η πλανητική υποβοήθηση, που βασίζεται στο ότι αν ένα διαστημόπλοιο πλησιάσει «μετωπικά» έναν πλανήτη με μικρή γωνία ως προς την κατεύθυνση κίνησής του, μπει σε τροχιά γύρω του για μισή περίπου περιστροφή και εκτοξευτεί σχετικά αντίθετα από την κατεύθυνση από την οποία ήλθε, μπορεί να προσθέσει στην αρχική ταχύτητά του, μέχρι και δύο φορές τη γραμμική ταχύτητα του πλανήτη. Στην πράξη βέβαια, η αλλαγή πορείας του διαστημοπλοίου δεν είναι τόσο ακραία, αλλά τόση όση χρειάζεται για το επιθυμητό αποτέλεσμα. Με αντίστοιχο τρόπο, μπορεί να γίνει και "φρενάρισμα" των διαστημοπλοίων προκειμένου να μπουν σε τροχιά γύρω από τους εσωτερικούς (ως προς τη Γη) πλανήτες του Ηλιακού Συστήματος.
Εφαρμογή του παραπάνω είναι η διαδρομή των δύο διαστημοσυσκευώνVoyager που αξιοποίησαν την βαρυτική έλξη των μεγάλων και μακρινών πλανητών για να αυξήσουν σημαντικά την ταχύτητά τους (διάγραμμα κάτω).
Υπόψη ότι στο διάγραμμα, η πράσινη γραμμή αντιστοιχεί στην ταχύτητα διαφυγής από το Ηλιακό Σύστημα (όχι μόνο από το βαρυτικό πεδίο της Γης). Μία AU (Astronomical Unit) αντιστοιχεί στην απόσταση Ήλιου - Γης.
51. Το «αλλόκοτο» φαινόμενο Mpemba.
Αφού υπέμενε για μερικά χρόνια τη σχετική «καζούρα», τελικά η επιμονή του νίκησε και η επιστημονική κοινότητα επιβεβαίωσε το φαινόμενο, δίνοντάς του μάλιστα το όνομα του παρατηρητικού μαθητή.
Ακόμα πιο περίεργο είναι ότι γεγονός ότι το φαινόμενο αυτό ήταν γνωστό από την εποχή του Αριστοτέλη, αλλά αγνοήθηκε από τους μεταγενέστερους, μάλλον επειδή δεν μπορούσαν να το εξηγήσουν!
Βέβαια το φαινόμενο δεν παρατηρείται πάντοτε, χωρίς να έχουν προσδιοριστεί ακριβώς ούτε οι συνθήκες στις οποίες συμβαίνει ούτε να έχει δοθεί τελείως ικανοποιητική εξήγηση γιατί συμβαίνει.
Η καλύτερη εξήγηση πάντως είναι ότι προκαλείται από τα διαλυμένα αέρια στο νερό, που επειδή διαφεύγουν ευκολότερα στις υψηλότερες θερμοκρασίες, καθιστούν το θερμό νερό πιο ομοιογενές ή "συμπαγές", επιτρέποντας τη γρηγορότερη ψύξη του. Σ’ αυτό συνηγορεί και το γεγονός ότι το φαινόμενο γίνεται τόσο πιο έντονο, όσο περισσότερο αέριο περιέχει αρχικά το νερό.
Κάτι αντίστοιχο συμβαίνει και όταν το νερό είναι πολύ καθαρό ή απεσταγμένο*, οπότε μπορεί να παραμείνει υγρό σε χαμηλότερη θερμοκρασία από τους 0ο Kελσίου, και να παγώσει απότομα από μια διαταραχή (κούνημα του δοχείου, πρόσκρουση «υπέρψυχρων» σταγόνων σε επιφάνεια κλπ).
*Το συνηθισμένο νερό περιέχει αρκετή ποσότητα αερίων, που δίνουν «γαλακτερή» όψη στον πάγο. Νερό απαλλαγμένο από αέρια (πχ με προηγούμενη θέρμανση), δίνει τελείως διάφανο πάγο.
52. Πετάει ο βάτραχος;
Πετάει!, αν και το ακριβέστερο είναι ότι αιωρείται, αρκεί το μαγνητικό πεδίο να είναι αρκετά ισχυρό (τουλάχιστον 15 Τ, που είναι ΠΟΛΥ ισχυρό * και δημιουργείται με ειδικά δισκοειδή πηνία, που ονομάζεται πηνία Bitter).
Στις συνθήκες αυτές, ακόμα και τα μη μαγνητικά (διαμαγνητικά) υλικά όπως το νερό αντιδρούν στο μαγνητικό πεδίο και μάλιστα με τρόπο ώστε να απωθούνται απ' αυτό **, οπότε ακόμα και ένας ζωντανός βάτραχος μπορεί να αιωρηθεί χωρίς δυσμενείς επιπτώσεις για την υγεία του.
* Για σύγκριση, ο ισχυρότερος μόνιμος μαγνήτης δεν ξεπερνά το 1.5 Τ, τα μαγνητικά πεδία των ηλεκτρομαγνητών στο CERN δεν ξεπερνούν τα 10 T, ενώ το ισχυρότερο μαγνητικό πεδίο που έχει δημιουργηθεί (από πηνία Bitter) είναι 45 Τ.
** Αντίθετα, τα υλικά από σίδηρο (σιδηρομαγνητικά) αλλά και τα λιγότερο μαγνητικά (παραμαγνητικά), αντιδρούν με τρόπο ώστε να έλκονται από το μαγνητικό πεδίο.
53. Η Φύση αγαπάει την "αταξία"!
Όπως λοιπόν, εάν μια εδαφική περιοχή αφεθεί μόνο στις δυνάμεις της διάβρωσης θα καταλήξει επίπεδη μετά από ΠΟΛΥ χρόνο, έτσι και ενεργειακά ένα σύστημα θα καταλήξει μακροχρόνια σε πλήρη «αταξία», καθώς όλο και μεγαλύτερο μέρος της ενέργειάς του θα υποβαθμίζεται σε θερμότητα, δηλαδή σε άτακτη κίνηση των μορίων του.
Μέτρο αυτής της αταξίας είναι η ελληνική λέξη Εντροπία (από το εν + τροπή) που χρησιμοποιείται διεθνώς και συνιστά μία από τις σημαντικότερες λέξεις της Θερμοδυναμικής.
Ένα απλό παράδειγμα είναι μια τάξη με ζωηρούς μαθητές.
Χρειάζεται προσπάθεια (έργο) από την πλευρά του δάσκαλου για να βάλει (ή να επαναφέρει) τους μαθητές σε τάξη, αλλά στην πρώτη ευκαιρία οι μαθητές του θα επιβεβαιώσουν περίτρανα την τάση ενός συστήματος να ρέπει προς την αύξηση της Εντροπίας του.
Μια δεύτερη σημαντική ελληνική (και επίσης διεθνής) λέξη στον τομέα της Θερμοδυναμικής είναι και η Ενθαλπία (εν + θάλπω*), που είναι το μέτρο της περιεχόμενης θερμικής ενέργειας ενός συστήματος.
Υπόψη ότι και οι δύο αυτές ελληνικές λέξεις έχουν καθιερωθεί από ξένους επιστήμονες (Clausius και Onnes αντίστοιχα).
54. H Θάτσερ και το μποζόνιο του Higgs.
Το μποζόνιο του Higgs έχει μια ενδιαφέρουσα ιστορία.
Κατ’ αρχή προβλέφθηκε από τον Higgs μαζί με άλλους συναδέλφους του το 1964, επιβεβαιώθηκε από το CERN το 2012, ενώ το επόμενο έτος ο Higgs και ένας άλλος συνάδελφός του μοιράστηκαν το βραβείο Νόμπελ για τη Φυσική.
Ένα μποζόνιο, είναι ένα υποατομικό σωματίδιο που «μεταφέρει» μια ιδιότητα και το συγκεκριμένο του Higgs είναι αυτό που θεωρείται ότι δίνει στην ύλη την ιδιότητα της μάζας, δηλαδή της αδράνειας.
Συχνά το μποζόνιο αυτό αναφέρεται και σαν το «σωματίδιο του Θεού» και το πώς απέκτησε αυτό το όνομα έχει ενδιαφέρον.
Ο Φυσικός Leon Lederman*, γράφοντας ένα βιβλίο για το σωματίδιο αυτό το 1993 ήθελε να του δώσει σαν τίτλο «The Goddamn Particle» δηλαδή «το διαβολεμένο σωματίδιο». Ο εκδότης του όμως διαφώνησε, οπότε ο Lederman περιέκοψε τον τίτλο στο «The God Particle» και η ονομασία αυτή παρέμεινε.
Κάτι άλλο ενδιαφέρον, έχει να κάνει με το γεγονός ότι το 1993 ο τότε Βρετανός υπουργός Επιστημών ζήτησε από τους συνεργάτες του μια απλοποιημένη περιγραφή για τον τρόπο που δρα το σωματίδιο Higgs.
H καλύτερη απάντηση που δόθηκε και έκτοτε χρησιμοποιείται συχνά, ήταν η παρακάτω:
«Φανταστείτε ότι η Θάτσερ (πρώην πρωθυπουργός εκείνη την εποχή, αλλά ακόμα δημοφιλής) μπαίνει σε μια συγκέντρωση πολιτικών.
Καθώς κινείται φαίνεται να διαθέτει μεγάλη μάζα, επειδή όλοι συγκεντρώνονται γύρω της, οπότε όσον κινείται είναι δύσκολο να σταματήσει και εφόσον σταματήσει δύσκολα ξεκινάει πάλι. Το ίδιο θα συμβεί αν δεν είναι η ίδια η Θάτσερ παρούσα, αλλά μια φήμη (πεδίο) που την αφορά και που εξαπλώνεται με παρόμοιο τρόπο».
* Ο Lederman (που είναι Αμερικανός) έχει πει και το εξής, σε σχέση με τη "γλυκόπικρη" αίσθηση που άφηνε η διαφαινόμενη νίκη του Cern έναντι των αμερικανικών ινστιτούτων, στην «κούρσα» για τον εντοπισμό του σωματιδίου Higgs:
«Είναι σαν να βλέπεις την πεθερά σου να πέφτει στον γκρεμό, οδηγώντας το αγαπημένο σου αυτοκίνητο!»
55. Ζάρια ή ταχυδακτυλουργικά;
55. Ζάρια ή ταχυδακτυλουργικά;
Είναι γνωστή η φράση του Αϊνστάιν «ο Θεός δεν παίζει ζάρια με το Σύμπαν»,
καθώς δεν του άρεσε η απροσδιοριστία που είναι η «κεντρική ιδέα» της Κβαντομηχανικής.
Μήπως όμως, «ο Θεός κάνει ταχυδακτυλουργικά»?
Μήπως δηλαδή κάποιες ιδιότητες μεταδίδονται «παρακάμπτοντας» τους (γνωστούς) φυσικούς νόμους?
Και αναφερόμαστε στο πιο παράδοξο από τα (ούτως ή άλλως) παράδοξα φαινόμενο της Κβαντομηχανικής, την «κβαντική εμπλοκή», (ή διεμπλοκή) ή «κβαντικό συσχετισμό», ή στα αγγλικά «quantum entanglement», το οποίο ο Αϊνστάιν χαρακτήριζε σαν «spooky action at a distance», δηλαδή «εξώκοσμη δράση από απόσταση».
Και όχι αναίτια, καθώς αυτό είναι το μόνο γνωστό φαινόμενο που μοιάζει να περιγελά το «θέσφατο» της Φυσικής, το όριο της ταχύτητας του φωτός στο κενό.
Η κβαντική εμπλοκή, συνδέει δύο αρχικά συσχετισμένα σωματίδια με ένα είδος «μη φυσικού δεσμού», ώστε η εν συνεχεία απομάκρυνσή τους να μην προκαλεί ούτε την εξασθένιση, ούτε την καθυστέρηση στην αλλαγή μιας συγκεκριμένης κατάστασης στο ένα, εφόσον η αντίστοιχη κατάσταση έχει μεταβληθεί στο άλλο.
Ο συσχετισμός αυτός γίνεται ακαριαία, ή τουλάχιστον τόσο γρήγορα ώστε δεν είναι δυνατόν να μετρηθεί κάποια καθυστέρηση.
Η κβαντική εξήγηση του φαινομένου (που είναι συμβατή με την μη υπέρβαση του ορίου της ταχύτητας του φωτός), βασίζεται στην απροσδιοριστία που κυριαρχεί στα σωματίδια όσο δεν τα παρατηρεί (ή δεν τα μετράει) κάποιος.
Δύο συσχετισμένα κβαντικά σωματίδια όμως (συνήθως φωτόνια), έχουν συσχετισμένες και τις απροσδιοριστίες τους, οπότε μόλις το ένα παρατηρηθεί και αρθεί η απροσδιοριστία του»*, το ίδιο (άρση της απροσδιοριστίας) θα συμβεί ακαριαία και στο δεύτερο, ανεξάρτητα της απόστασής του.
Οι πιθανές επιπτώσεις από την αξιοποίηση αυτού του φαινομένου είναι πολλές και σημαντικές, από τις πλέον ευφάνταστες, όπως η τηλεμεταφορά αντικειμένων ακόμα και ζωντανών οργανισμών, μέχρι τις πιο προσγειωμένες, όπως στην αύξηση της ταχύτητας επεξεργασίας δεδομένων των κβαντικών υπολογιστών, καθώς η κβαντική εμπλοκή δεν μπορεί να χρησιμοποιηθεί για τη μεταφορά πληροφοριών, επειδή δεν συμβαίνει μεταφορά ενέργειας.
* Στη γλώσσα της Κβαντομηχανικής: «όταν καταρρεύσει η κυματοσυνάρτησή του».
Θα σας περνούσε ποτέ από μυαλό να τρέξετε πάνω σ’ ένα «υγρό», που ακόμα και ακίνητος να μένατε επάνω του, θα βουλιάζατε?
Και όμως αυτή η προφανώς παράλογη σκέψη είναι απολύτως σωστή, αν πρόκειται για μια κατηγορία υγρών που ονομάζονται «μη Νευτώνια».
Και μην φανταστείτε ότι τα μη Νευτώνια είναι κάτι το εξωτικό, ένα τέτοιο υγρό για παράδειγμα είναι καλαμποκάλευρο διαλυμένο σε νερό!
Η ιδιοτροπία αυτών των υγρών οφείλεται στο ότι όταν κάτι κινείται με μικρή ταχύτητα μέσα στη μάζα τους, εμφανίζουν σχετικά μικρή αντίσταση, ενώ όσο η ταχύτητα αυξάνεται τόσο συμπεριφέρονται σαν πιο «συμπαγή».
Μια τεχνολογική εφαρμογή αυτού του φαινόμενου είναι οι «viscocouplers», αυτόματοι συμπλέκτες με μη Νευτώνιο σιλικονούχο υγρό μέσα τους, που «σφίγγουν» όσο μεγαλώνει η σχετική ταχύτητα των δύο ροτόρων που συνδέονται με τους άξονες εισόδου και εξόδου.
Δεν «σφίγγουν» όμως όλα τα μη Νευτώνια υγρά όταν πιεστούν.
Κάποια εμφανίζουν ακριβώς την αντίθετη συμπεριφορά, όπως το κέτσαπ!
57. Σπηλαίωση. Πρόβλημα ή λύση;
- Ένα Σύμπαν από το Τίποτα.
- Η ενέργεια του Απόλυτου Κενού.
Οι παραπάνω θέσεις της Σύγχρονης Φυσικής μοιάζουν απίθανες και παράλογες και αντίκεινται στην εμπειρία μας και κατά συνέπεια και στη λογική μας, όμως η Σύγχρονη Φυσική τις εξετάζει γιατί δεν έρχονται σε αντίθεση με τα μαθηματικά της.
Το νερό είναι η πιο κοινή, πιο γνωστή, αλλά ταυτόχρονα και η πιο περίεργη ουσία στη Γη.
Η παραδοξότητά της οφείλεται βασικά στο γεγονός ότι το μόριο του νερού δεν είναι συμμετρικό, αλλά τα δύο άτομα του υδρογόνου σχηματίζουν μια ανοικτή γωνία μεταξύ τους έχοντας το άτομο του οξυγόνου ανάμεσά τους, με αποτέλεσμα να παρουσιάζουν ηλεκτρική πόλωση.
Σε αυτή την ιδιότητα χρωστάει το νερό την επιφανειακή τάση που αναπτύσσει (σαν να το περιβάλλει μια λεπτή μεμβράνη), αλλά και το γεγονός ότι παραμένει υγρό στις συνηθισμένες θερμοκρασίες, ενώ ακόμα και σημαντικά βαρύτερα μόρια είναι αέρια.
Η ιδιότητα όμως του νερού με τη σημαντικότερη επίπτωση στη ζωή στη Γη είναι ότι η πυκνότητα του μειώνεται κάτω από τους 4ο C, με αποτέλεσμα ο πάγος να επιπλέει και οι υδάτινοι όγκοι να παγώνουν μόνο επιφανειακά, προστατεύοντας τη ζωή στο βάθος τους.
Επίσης, το σημείο βρασμού του είναι ιδιαίτερα υψηλό και για να μετατραπεί σε αέριο απορροφά σημαντική ποσότητα θερμότητας (λανθάνουσα θερμότητα), η οποία αποδίδεται αντίστοιχα κατά την υγροποίησή του (πολύ χρήσιμο στις ατμομηχανές).
Ακόμα, είναι με διαφορά το πιο αποτελεσματικό διαλυτικό όλων σχεδόν των ουσιών της γης, ενώ είναι διαφανές μόνο στο ορατό τμήμα του ηλεκτρομαγνητικού φάσματος (μην περιμένετε λοιπόν να μαυρίσετε μέσα στο νερό).
Τέλος, ρίξτε μια ματιά στο φαινόμενο Mpemba (θέμα Νο 51), για να διαπιστώστε ότι το νερό έχει και άλλους «άσσους» στο μανίκι του!
Είναι γνωστό ότι ο ενεργειακός βαθμός απόδοσης μιας συσκευής, που είναι ο λόγος της προσφερόμενης ενέργειας στο σύστημα προς την αποδιδόμενη ενέργεια παραμένει πάντα μικρότερος από τη μονάδα, δηλαδή μικρότερος από 100%, γι’ αυτό δεν πρόκειται ποτέ να υπάρξει το αεικίνητο.
Κάποιες μάλιστα συσκευές που οι εφευρέτες τους ισχυρίζονταν ότι ήταν «αεικίνητα», αποδείχθηκε ότι στην πραγματικότητα έπαιρναν ενέργεια από το περιβάλλον σαν θερμότητα, φως κλπ.
Υπάρχει όμως μια συσκευή η οποία όχι μόνο ξεπερνάει σε ενεργειακή απόδοση το 100%, αλλά φθάνει στο 300% ή και περισσότερο!
Και μάλιστα δεν πρόκειται για κάποια «εξωτική» συσκευή αλλά για την αντλία θερμότητας που βρίσκεται στην καρδιά κάθε κλιματιστικού συστήματος.
Η αιτία για μια τέτοια φαινομενικά εξωπραγματική απόδοση είναι ότι η αντλία θερμότητας δεν χρησιμοποιεί την ηλεκτρική ενέργεια με την οποία την τροφοδοτούμε για να τη μετατρέψει σε θερμότητα, όπως πχ κάνει μία ηλεκτρική θερμάστρα, αλλά για να μεταφέρει θερμότητα από μία περιοχή σε μία άλλη.
Μάλιστα, αν χρησιμοποιηθεί το έδαφος σαν δεξαμενή θερμότητας (γεωεναλλάκτης) αντί του αέρα, ο βαθμός απόδοσης μιας σύγχρονης αντλίας θερμότητας (με inverter) μπορεί να φθάσει και το 500%!
Επειδή έχουν πολύ μεγαλύτερη θερμική αγωγιμότητα από τα υπόλοιπα υλικά και οι υποδοχείς στο δέρμα μας ερμηνεύουν την αίσθηση ανάλογα με την ένταση και τη φορά της ροής της θερμότητας κατά την επαφή, σαν περισσότερο κρύο ή ζέστη.
Όμως για να συμβεί αυτό δηλαδή ροή θερμότητας, θα πρέπει το αντικείμενο που ακουμπάμε να έχει διαφορετική θερμοκρασία από αυτή του σώματός μας (36ο C), κάτι που βέβαια συνήθως ισχύει καθώς η θερμοκρασία των χώρων και των αντικειμένων είναι σχεδόν πάντα χαμηλότερη από αυτή του σώματός μας, γεγονός που ερμηνεύεται από τον εγκέφαλό μας σαν κρύο.
Είναι γνωστό ότι οι δυνάμεις διαστολής και συστολής είναι πολύ μεγάλες και ειδικά στα στερεά προκαλούν σοβαρές παραμορφώσεις εάν εμποδιστούν.
Πόσο μεγάλες όμως είναι αυτές οι δυνάμεις?
Μια ιδέα του μεγέθους τους παίρνουμε αν τις θεωρήσουμε ίσες με τις δυνάμεις που απαιτούνται για να επιφέρουμε την ίδια παραμόρφωση, χωρίς αύξηση της θερμοκρασίας του υλικού.
Για παράδειγμα, η δύναμη που θα ασκήσει ένα κομμάτι σίδερο που θα εμποδιστεί να διασταλεί εφόσον θερμανθεί, είναι ίση με τη δύναμη που θα πρέπει να εφαρμόσουμε για να το επιμηκύνουμε κατά το ίδιο ποσοστό τεντώνοντάς το μηχανικά, χωρίς να το θερμάνουμε.
Ακούγεται παράδοξο ένα ιστιοφόρο να μπορεί να κινηθεί ταχύτερα από το ίδιο τον άνεμο και πράγματι αυτό είναι αδύνατον στην ούρια πλεύση, δηλαδή όταν ο άνεμος έρχεται από την πρύμνη και σπρώχνει το πανί σαν ένα εμπόδιο.
56. Μη Νευτώνια ρευστά.
Και όμως αυτή η προφανώς παράλογη σκέψη είναι απολύτως σωστή, αν πρόκειται για μια κατηγορία υγρών που ονομάζονται «μη Νευτώνια».
Και μην φανταστείτε ότι τα μη Νευτώνια είναι κάτι το εξωτικό, ένα τέτοιο υγρό για παράδειγμα είναι καλαμποκάλευρο διαλυμένο σε νερό!
Η ιδιοτροπία αυτών των υγρών οφείλεται στο ότι όταν κάτι κινείται με μικρή ταχύτητα μέσα στη μάζα τους, εμφανίζουν σχετικά μικρή αντίσταση, ενώ όσο η ταχύτητα αυξάνεται τόσο συμπεριφέρονται σαν πιο «συμπαγή».
Μια τεχνολογική εφαρμογή αυτού του φαινόμενου είναι οι «viscocouplers», αυτόματοι συμπλέκτες με μη Νευτώνιο σιλικονούχο υγρό μέσα τους, που «σφίγγουν» όσο μεγαλώνει η σχετική ταχύτητα των δύο ροτόρων που συνδέονται με τους άξονες εισόδου και εξόδου.
Δεν «σφίγγουν» όμως όλα τα μη Νευτώνια υγρά όταν πιεστούν.
Κάποια εμφανίζουν ακριβώς την αντίθετη συμπεριφορά, όπως το κέτσαπ!
57. Σπηλαίωση. Πρόβλημα ή λύση;
Πρόκειται για ένα περίεργο φαινόμενο που σχετίζεται με τις δυναμικές ιδιότητες των υγρών, και ενώ συνήθως είναι πονοκέφαλος για τους Μηχανικούς, μπορεί να δώσει μια γιγάντια ώθηση στην ταχύτητα μετακίνησης μέσα στο νερό.
Το φαινόμενο αφορά τη δημιουργία φυσαλίδων κενού (ή περίπου κενού), ακριβώς πίσω από ένα εξάρτημα που κινείται με μεγάλη ταχύτητα μέσα στο νερό, εφόσον δημιουργείται πολύ έντονη υποπίεση στο σημείο αυτό.
Οι φυσαλίδες αυτές τελικά θα «σκάσουν προς τα μέσα», μόλις έχουν την ευκαιρία, δηλαδή μόλις η υποπίεση πάψει να είναι έντονη, αλλά τότε σταγονίδια νερού θα κινηθούν ταχύτητα να καταλάβουν τον χώρο, και με τη «φόρα» που έχουν θα προσκρούσουν στην επιφάνεια που επάνω της βρίσκονταν οι φυσαλίδες, σκάβοντάς την κυριολεκτικά.
Έτσι δημιουργείται σημαντική φθορά στα εξαρτήματα (συνήθως έλικες ή ρότορες), αλλά και πονοκέφαλος στους Μηχανικούς!
Η λύση βέβαια είναι καλύτερη σχεδίαση των εξαρτημάτων, και στην εποχή της σχεδίασης με υπολογιστή αυτό είναι εύκολο, οι Μηχανικοί όμως σκέφτηκαν να αξιοποιήσουν το φαινόμενο τραβώντας το στα άκρα.
Η ιδέα είναι να δημιουργήσουν επίτηδες σπηλαίωση στο ρύγχος ενός υδροδυναμικού και γρήγορα κινούμενου σώματος, οπότε οι φυσαλίδες από τη σπηλαίωση θα «καλύψουν» σαν μανδύας το σώμα, απομονώνοντάς το από την τριβή του με το νερό!
58. Γιατί τα κύματα είναι χρήσιμα;
Το φαινόμενο αφορά τη δημιουργία φυσαλίδων κενού (ή περίπου κενού), ακριβώς πίσω από ένα εξάρτημα που κινείται με μεγάλη ταχύτητα μέσα στο νερό, εφόσον δημιουργείται πολύ έντονη υποπίεση στο σημείο αυτό.
Οι φυσαλίδες αυτές τελικά θα «σκάσουν προς τα μέσα», μόλις έχουν την ευκαιρία, δηλαδή μόλις η υποπίεση πάψει να είναι έντονη, αλλά τότε σταγονίδια νερού θα κινηθούν ταχύτητα να καταλάβουν τον χώρο, και με τη «φόρα» που έχουν θα προσκρούσουν στην επιφάνεια που επάνω της βρίσκονταν οι φυσαλίδες, σκάβοντάς την κυριολεκτικά.
Έτσι δημιουργείται σημαντική φθορά στα εξαρτήματα (συνήθως έλικες ή ρότορες), αλλά και πονοκέφαλος στους Μηχανικούς!
Η λύση βέβαια είναι καλύτερη σχεδίαση των εξαρτημάτων, και στην εποχή της σχεδίασης με υπολογιστή αυτό είναι εύκολο, οι Μηχανικοί όμως σκέφτηκαν να αξιοποιήσουν το φαινόμενο τραβώντας το στα άκρα.
Η ιδέα είναι να δημιουργήσουν επίτηδες σπηλαίωση στο ρύγχος ενός υδροδυναμικού και γρήγορα κινούμενου σώματος, οπότε οι φυσαλίδες από τη σπηλαίωση θα «καλύψουν» σαν μανδύας το σώμα, απομονώνοντάς το από την τριβή του με το νερό!
58. Γιατί τα κύματα είναι χρήσιμα;
Εννοούμε φυσικά πέρα από το να επιτρέπουν στους σέρφερς να κάνουν τις θεαματικές φιγούρες τους, και να επιτρέπουν (προς το παρόν πειραματικά) και την παραγωγή ηλεκτρικής ενέργειας.
Τα παραπάνω ισχύουν βέβαια για τα θαλασσινά κύματα, τα οποία αποτελούν και την πιο οικεία εικόνα κυμάτων, καθώς τα άλλα είδη, δηλαδή τα ηχητικά και πολύ περισσότερο τα ηλεκτρομαγνητικά, είναι αόρατα.
Τα σταθερά και συνεχόμενα κύματα γενικά, είναι ένας από τους τρόπους της φύσης να μεταφέρει ενέργεια με ελεγχόμενο τρόπο.
Και λέμε με ελεγχόμενο τρόπο, γιατί και το κύμα από ένα τσουνάμι ή μια έκρηξη μεταφέρει ενέργεια και μάλιστα μεγάλη, αλλά προφανώς με καταστροφικό τρόπο.
Τη μεταφορά αυτής της ενέργειας στην περίπτωση των θαλασσινών κυμάτων μπορούμε να την καταλάβουμε από τους τρόπους με τους οποίους μπορεί να αξιοποιηθεί η ενέργειά τους, πχ με πλωτήρες που ανεβοκατεβαίνουν ή αρθρωτούς σωλήνες που κάμπτονται και ενεργοποιούν συστήματα παραγωγής ηλεκτρικής ενέργειας.
Ακόμα και την ενέργεια των ηχητικών κυμάτων μπορούμε να την καταλάβουμε σχετικά εύκολα, αρκεί να παρακολουθήσουμε τον κώνο ενός μεγάλου ηχείου χαμηλών συχνοτήτων να πάλλεται, ή από τον πόνο στα αυτιά μας εξαιτίας δυνατής μουσικής.
Τα ηλεκτρομαγνητικά κύματα από την άλλη πλευρά (εικόνα επάνω) είναι σχεδόν αδύνατον να τα ανιχνεύσουμε με τις αισθήσεις μας, εκτός από την φωτεινή ακτινοβολία φυσικά, αλλά είμαστε κυριολεκτικά βυθισμένοι μέσα σ’ αυτά εξαιτίας των εκπομπών τηλεόρασης, ραδιοφώνου, κινητών τηλεφώνων, ραντάρ κλπ.
Τα ηλεκτρομαγνητικά κύματα έχουν επίσης το μεγάλο πλεονέκτημα να μην χρειάζονται υλικό μέσο για τη μετάδοσή τους, μεταδίδονται μια χαρά (και ακόμα καλύτερα) στο κενό, αλλιώς για παράδειγμα το φως του Ήλιου δεν θα έφτανε ποτέ στη Γη.
Μέχρι τώρα πάντως, δεν έχει βρεθεί πρακτικός τρόπος να μεταφερθεί σημαντική ποσότητα ενέργειας με ηλεκτρομαγνητική ακτινοβολία (μεταφέρονται ουσιαστικά μόνο σήματα), και ο Τέσλα που επιχείρησε να κατασκευάσει ένα τέτοιο σύστημα στις αρχές του 20ου αιώνα, δεν μπόρεσε να το ολοκληρώσει.
Τα παραπάνω ισχύουν βέβαια για τα θαλασσινά κύματα, τα οποία αποτελούν και την πιο οικεία εικόνα κυμάτων, καθώς τα άλλα είδη, δηλαδή τα ηχητικά και πολύ περισσότερο τα ηλεκτρομαγνητικά, είναι αόρατα.
Τα σταθερά και συνεχόμενα κύματα γενικά, είναι ένας από τους τρόπους της φύσης να μεταφέρει ενέργεια με ελεγχόμενο τρόπο.
Και λέμε με ελεγχόμενο τρόπο, γιατί και το κύμα από ένα τσουνάμι ή μια έκρηξη μεταφέρει ενέργεια και μάλιστα μεγάλη, αλλά προφανώς με καταστροφικό τρόπο.
Τη μεταφορά αυτής της ενέργειας στην περίπτωση των θαλασσινών κυμάτων μπορούμε να την καταλάβουμε από τους τρόπους με τους οποίους μπορεί να αξιοποιηθεί η ενέργειά τους, πχ με πλωτήρες που ανεβοκατεβαίνουν ή αρθρωτούς σωλήνες που κάμπτονται και ενεργοποιούν συστήματα παραγωγής ηλεκτρικής ενέργειας.
Ακόμα και την ενέργεια των ηχητικών κυμάτων μπορούμε να την καταλάβουμε σχετικά εύκολα, αρκεί να παρακολουθήσουμε τον κώνο ενός μεγάλου ηχείου χαμηλών συχνοτήτων να πάλλεται, ή από τον πόνο στα αυτιά μας εξαιτίας δυνατής μουσικής.
Τα ηλεκτρομαγνητικά κύματα από την άλλη πλευρά (εικόνα επάνω) είναι σχεδόν αδύνατον να τα ανιχνεύσουμε με τις αισθήσεις μας, εκτός από την φωτεινή ακτινοβολία φυσικά, αλλά είμαστε κυριολεκτικά βυθισμένοι μέσα σ’ αυτά εξαιτίας των εκπομπών τηλεόρασης, ραδιοφώνου, κινητών τηλεφώνων, ραντάρ κλπ.
Τα ηλεκτρομαγνητικά κύματα έχουν επίσης το μεγάλο πλεονέκτημα να μην χρειάζονται υλικό μέσο για τη μετάδοσή τους, μεταδίδονται μια χαρά (και ακόμα καλύτερα) στο κενό, αλλιώς για παράδειγμα το φως του Ήλιου δεν θα έφτανε ποτέ στη Γη.
Μέχρι τώρα πάντως, δεν έχει βρεθεί πρακτικός τρόπος να μεταφερθεί σημαντική ποσότητα ενέργειας με ηλεκτρομαγνητική ακτινοβολία (μεταφέρονται ουσιαστικά μόνο σήματα), και ο Τέσλα που επιχείρησε να κατασκευάσει ένα τέτοιο σύστημα στις αρχές του 20ου αιώνα, δεν μπόρεσε να το ολοκληρώσει.
59. Τρείς απίθανες θέσεις της Σύγχρονης Φυσικής.
- Η ενέργεια του Απόλυτου Κενού.
- Ο Χρόνος που γυρίζει πίσω.
Οι παραπάνω θέσεις της Σύγχρονης Φυσικής μοιάζουν απίθανες και παράλογες και αντίκεινται στην εμπειρία μας και κατά συνέπεια και στη λογική μας, όμως η Σύγχρονη Φυσική τις εξετάζει γιατί δεν έρχονται σε αντίθεση με τα μαθηματικά της.
Αφού στο παρελθόν οι επιστήμονες την «πάτησαν» αρκετές φορές βάζοντας αυθαίρετα όρια σε διάφορα φυσικά φαινόμενα ή δυνατότητες και στη συνέχεια διαψεύσθηκαν πανηγυρικά, πλέον απορρίπτουν μόνο ότι αντιβαίνει στα μαθηματικά της Φυσικής, ενώ όλα τα άλλα, όσο περίεργα και αν ακούγονται, εξετάζονται.
- Η γέννηση λοιπόν ενός ολόκληρου Σύμπαντος (ακόμα και πολλών Συμπάντων) από το Τίποτα μπορεί να συμβεί αυθόρμητα και χωρίς κανένα πρόβλημα, εφόσον το σύνολο της θετικής ενέργειας (που περιλαμβάνει και την ύλη) ισούται με το σύνολο της αρνητικής ενέργειας που εκδηλώνεται με τη βαρύτητα.
Για παράδειγμα, πρέπει να καταβάλουμε ενέργεια για να σηκώσουμε ένα αντικείμενο, εργαζόμενοι αντίθετα προς την ενέργεια της βαρύτητας.
- Στο απόλυτο κενό, υποατομικά σωματίδια (αλλά και ενεργειακά πεδία) ξεπηδούν από το μηδέν, διασπώνται, συγχωνεύονται και εξαφανίζονται, κάνοντάς το να μοιάζει πιο πολύ με καζάνι που βράζει, παρά με χώρο που «δεν περιέχει τίποτα» σύμφωνα με την κλασική Φυσική.
- ‘Οσο για τον χρόνο, τίποτα δεν τον εμποδίζει να πάει προς τα πίσω, όχι πάντως οι εξισώσεις της Φυσικής. Αυτό θα μπορούσαμε να το καταλάβουμε καλύτερα, αν κάνουμε ένα διανοητικό πείραμα.
Ας θεωρήσουμε ότι παρακολουθούμε σε κινηματογραφική ταινία (ή βίντεο) μία επιφάνεια μπιλιάρδου χωρίς όρια. Στο κέντρο είναι στημένες στην τριγωνική διάταξη εκκίνησης οι μπίλιες, και ξαφνικά μια μπίλια εμφανίζεται από κάπου και χτυπάει με δύναμη τις συγκεντρωμένες μπίλιες, στέλνοντάς τες προς όλες τις κατευθύνσεις.
Ας φανταστούμε τώρα μια δεύτερη σκηνή.
Βλέπουμε (σε ταινία ή βίντεο) μια άδεια επιφάνεια μπιλιάρδου, και ξαφνικά έρχονται μπίλιες από διάφορες κατευθύνσεις και συγκεντρώνονται σ’ ένα σφικτό τέλειο τρίγωνο, εκτοξεύοντας ταυτόχρονα και μία μπίλια προς τα έξω.
Είναι προφανώς λογικό να σκεφτούμε ότι η πρώτη σκηνή είναι παιγμένη προς την σωστή χρονική κατεύθυνση, ενώ η δεύτερη είναι παιγμένη ανάποδα.
Όμως κανένας φυσικός νόμος δεν εμποδίζει να συμβεί το γεγονός της δεύτερης σκηνής, απλά θα πρέπει «κάποιος» να υπολογίσει τις γωνίες, τις θέσεις και τις ταχύτητες των μπιλιών με πολύ μεγάλη ακρίβεια (άρα να καταβάλει σημαντική ενέργεια)* και στη συνέχεια να τις εκτοξεύσει ώστε να κινηθούν αντίθετα προς την αύξηση της «εντροπίας» τους (δηλαδή της αταξίας τους), που στον κόσμο μας καθορίζει τη φυσιολογική φορά της ροής του χρόνου.
Συνεπώς, το να μην είναι παιγμένη ανάποδα η δεύτερη σκηνή δεν είναι αδύνατον, απλά είναι εξαιρετικά απίθανο.
*Και όμως αυτό ακριβώς συμβαίνει στο CERN, όπου οι επιστήμονες παίζουν «ανάποδο μπιλιάρδο» συστηματικά. Συνθέτουν τις τροχιές και ταχύτητες των σωματιδίων που προκύπτουν από τις διασπάσεις στον επιταχυντή, για να καθορίσουν τις ιδιότητες των αρχικών σωματιδίων.
60. Το νερό, ένα «μαγικό» υγρό.
Η παραδοξότητά της οφείλεται βασικά στο γεγονός ότι το μόριο του νερού δεν είναι συμμετρικό, αλλά τα δύο άτομα του υδρογόνου σχηματίζουν μια ανοικτή γωνία μεταξύ τους έχοντας το άτομο του οξυγόνου ανάμεσά τους, με αποτέλεσμα να παρουσιάζουν ηλεκτρική πόλωση.
Σε αυτή την ιδιότητα χρωστάει το νερό την επιφανειακή τάση που αναπτύσσει (σαν να το περιβάλλει μια λεπτή μεμβράνη), αλλά και το γεγονός ότι παραμένει υγρό στις συνηθισμένες θερμοκρασίες, ενώ ακόμα και σημαντικά βαρύτερα μόρια είναι αέρια.
Η ιδιότητα όμως του νερού με τη σημαντικότερη επίπτωση στη ζωή στη Γη είναι ότι η πυκνότητα του μειώνεται κάτω από τους 4ο C, με αποτέλεσμα ο πάγος να επιπλέει και οι υδάτινοι όγκοι να παγώνουν μόνο επιφανειακά, προστατεύοντας τη ζωή στο βάθος τους.
Επίσης, το σημείο βρασμού του είναι ιδιαίτερα υψηλό και για να μετατραπεί σε αέριο απορροφά σημαντική ποσότητα θερμότητας (λανθάνουσα θερμότητα), η οποία αποδίδεται αντίστοιχα κατά την υγροποίησή του (πολύ χρήσιμο στις ατμομηχανές).
Ακόμα, είναι με διαφορά το πιο αποτελεσματικό διαλυτικό όλων σχεδόν των ουσιών της γης, ενώ είναι διαφανές μόνο στο ορατό τμήμα του ηλεκτρομαγνητικού φάσματος (μην περιμένετε λοιπόν να μαυρίσετε μέσα στο νερό).
Τέλος, ρίξτε μια ματιά στο φαινόμενο Mpemba (θέμα Νο 51), για να διαπιστώστε ότι το νερό έχει και άλλους «άσσους» στο μανίκι του!
61. Βαθμός απόδοσης 300%;
Κάποιες μάλιστα συσκευές που οι εφευρέτες τους ισχυρίζονταν ότι ήταν «αεικίνητα», αποδείχθηκε ότι στην πραγματικότητα έπαιρναν ενέργεια από το περιβάλλον σαν θερμότητα, φως κλπ.
Υπάρχει όμως μια συσκευή η οποία όχι μόνο ξεπερνάει σε ενεργειακή απόδοση το 100%, αλλά φθάνει στο 300% ή και περισσότερο!
Και μάλιστα δεν πρόκειται για κάποια «εξωτική» συσκευή αλλά για την αντλία θερμότητας που βρίσκεται στην καρδιά κάθε κλιματιστικού συστήματος.
Η αιτία για μια τέτοια φαινομενικά εξωπραγματική απόδοση είναι ότι η αντλία θερμότητας δεν χρησιμοποιεί την ηλεκτρική ενέργεια με την οποία την τροφοδοτούμε για να τη μετατρέψει σε θερμότητα, όπως πχ κάνει μία ηλεκτρική θερμάστρα, αλλά για να μεταφέρει θερμότητα από μία περιοχή σε μία άλλη.
Μάλιστα, αν χρησιμοποιηθεί το έδαφος σαν δεξαμενή θερμότητας (γεωεναλλάκτης) αντί του αέρα, ο βαθμός απόδοσης μιας σύγχρονης αντλίας θερμότητας (με inverter) μπορεί να φθάσει και το 500%!
62. Γιατί τα μεταλλικά αντικείμενα είναι κρύα στην αφή;
Όμως για να συμβεί αυτό δηλαδή ροή θερμότητας, θα πρέπει το αντικείμενο που ακουμπάμε να έχει διαφορετική θερμοκρασία από αυτή του σώματός μας (36ο C), κάτι που βέβαια συνήθως ισχύει καθώς η θερμοκρασία των χώρων και των αντικειμένων είναι σχεδόν πάντα χαμηλότερη από αυτή του σώματός μας, γεγονός που ερμηνεύεται από τον εγκέφαλό μας σαν κρύο.
63. Δυνάμεις διαστολής.
Πόσο μεγάλες όμως είναι αυτές οι δυνάμεις?
Μια ιδέα του μεγέθους τους παίρνουμε αν τις θεωρήσουμε ίσες με τις δυνάμεις που απαιτούνται για να επιφέρουμε την ίδια παραμόρφωση, χωρίς αύξηση της θερμοκρασίας του υλικού.
Για παράδειγμα, η δύναμη που θα ασκήσει ένα κομμάτι σίδερο που θα εμποδιστεί να διασταλεί εφόσον θερμανθεί, είναι ίση με τη δύναμη που θα πρέπει να εφαρμόσουμε για να το επιμηκύνουμε κατά το ίδιο ποσοστό τεντώνοντάς το μηχανικά, χωρίς να το θερμάνουμε.
64. Ιστοφόρο ταχύτερο από τον άνεμο;
Φυσικά για χιλιάδες χρόνια τα ιστιοφόρα ταξίδευαν με αυτόν τον τρόπο, γι’ αυτόν τον λόγο ο ούριος άνεμος ήταν τόσο επιθυμητός.
Στα σύγχρονα όμως ιστιοφόρα το πανί χρησιμοποιείται σαν κατακόρυφα τοποθετημένη πτέρυγα και αξιοποιείται καλύτερα όταν ο άνεμος έρχεται από τα πλάγια του σκάφους, οπότε το πανί τον εκτρέπει αεροδυναμικά λοξά προς τα πίσω.
Αυτή η αλλαγή κατεύθυνσης του ανέμου δημιουργεί λοξή προς τα εμπρός ώση επάνω στο πανί και κατ’ επέκταση στο σκάφος.
Απαραίτητη προϋπόθεση όμως για την αξιοποίηση αυτών των λοξών δυνάμεων που αναπτύσσονται επάνω στο σκάφος είναι η ύπαρξη μιας μεγάλης σε επιφάνεια καρίνας που «κόβει» την πλευρική κίνηση του σκάφους και επιτρέπει ουσιαστικά μόνο την κίνηση κατά τον διαμήκη άξονά του.
Έτσι, καθώς η κίνηση του σκάφους γίνεται κάθετα προς τον τοπικό άνεμο (βέβαια ο φαινόμενος άνεμος επηρεάζεται από την κίνηση του σκάφους), ένα καλοσχεδιασμένο αγωνιστικό ιστιοφόρο μπορεί να κινηθεί με ταχύτητα στο νερό μεγαλύτερη από την ταχύτητα του τοπικού ανέμου ως προς το νερό.
Αυτό είναι ιδιαίτερα εμφανές σε αγωνιστικά υδροπτέρυγα καταμαράν (εικόνα επάνω), στα οποία ελάχιστο μέρος του σκάφους έρχεται σε επαφή με το νερό, και τα οποία μπορούν να ξεπεράσουν άνετα το διπλάσιο της ταχύτητας του ανέμου που τα κινεί.
ΥΓ1. (Δεκ. 2021) Και όμως ένα όχημα μπορεί να κινηθεί ταχύτερα, και στην ίδια κατεύθυνση, από τον άνεμο που το σπρώχνει (τουλάχιστον αυτό έχει επιδειχθεί σε όχημα, αναζητείστε το στο internet σαν blackbird wind car, εικόνα επάνω). Αν και φαίνεται αδύνατον εκ πρώτης όψης, πρόκειται για ένα ελαφρύ όχημα που οι τροχοί του κινούν μέσω οδόντωσης πολλαπλασιασμού στροφών μία έλικα, σχεδιασμένη να το προωθεί προς την κατεύθυνση που το σπρώχνει ο άνεμος. Από τη στιγμή που το όχημα αρχίζει να το κινείται σπρωγμένο από τον άνεμο, η έλικα (λειτουργώντας σαν έλικα αεροπλάνου) το επιταχύνει και αν οι τριβές είναι χαμηλές μπορεί άνετα να κινηθεί ταχύτερα από τον άνεμο, δηλαδή να συναντά τον (φαινόμενο) άνεμο από εμπρός!
ΥΓ2. Ένα αντίστοιχο παράδοξο φαινόμενο είναι η κίνηση της τορπίλης Brennan. Πατενταρισμένη το 1877(!) από τον Louis Brennan, η λειτουργία της γίνεται πιο εύκολα κατανοητή στο απλοποιημένο μοντέλο της εικόνας. Πηγή: https://www.printables.com/model/1087789-brennan-torpedo-dave-ansell
Ένα αντίστοιχο "παράδοξο" συμβαίνει όταν δέσουμε ένα σπάγκο στο πεντάλ ενός ποδηλάτου ενώ βρίσκεται στην κάτω θέση, και το τραβήξουμε προς τα πίσω. Ανάλογα με το γρανάζωμα (αν έχει πχ σχέση γραναζιών κατάλληλη για ανήφορο) θα κινηθεί εύκολα προς τα εμπρός.
65. 2000 βαθμοί Κελσίου, και όμως παγωνιά!
Πώς γίνεται όμως να κινούνται και να διαπερνούν τη ζώνη αυτή πύραυλοι και διαστημόπλοια με μεγάλη ταχύτητα χωρίς να παθαίνουν ζημιά;
Η απάντηση είναι ότι οι 2.000 βαθμοί αντιστοιχούν σε συγκεκριμένη κινητικότητα των μορίων της ατμόσφαιρας, που οφείλεται στην ανεμπόδιστη επίδραση της ακτινοβολίας του Ήλιου, κυρίως της υπεριώδους. Τα μόρια της ατμόσφαιρας όμως σ’ αυτά τα μεγάλα ύψη είναι τόσο απομακρυσμένα μεταξύ τους, που στην πραγματικότητα το αποτέλεσμα σ’ ένα αντικείμενο που θα βρεθεί σ’ αυτή την περιοχή, είναι η έντονη ψύξη του εξαιτίας της θερμικής ακτινοβολίας του!
(Βλ και θέμα Νο 93).
66. Χαμηλές και
υψηλές συχνότητες.
Από την εμπειρία μας είναι γνωστό ότι οι ήχοι χαμηλής
συχνότητας (μπάσα) ακούγονται πολύ περισσότερο και μεταδίδονται πολύ μακρύτερα
από τις υψηλές συχνότητες (πρίμα). Η Φυσική όμως λέει ότι οι υψηλές συχνότητες
μεταφέρουν μεγαλύτερη ισχύ και αυτό είναι φανερό στην ηλεκτρομαγνητική
ακτινοβολία, καθώς η υπεριώδης ακτινοβολία (από το οπτικό φάσμα), οι ακτίνες Χ
και ακόμα περισσότερο οι ακτίνες γ διαπερνούν και κάνουν ζημιά ανάλογα με τον
χρόνο έκθεσης, τους ανθρώπινους ιστούς.
Θα νόμιζε λοιπόν κανείς ότι τα ηχητικά κύματα
συμπεριφέρονται ανάποδα απ’ ότι η ηλεκτρομαγνητική ακτινοβολία. Όμως δεν είναι
έτσι. Σε κάθε περίπτωση η υψηλότερη συχνότητα (μικρότερο μήκος κύματος)
μεταφέρει μεγαλύτερη ισχύ, εφόσον το πλάτος της ταλάντωσης είναι το ίδιο. Αυτό που συμβαίνει με τα ηχητικά μπάσα είναι
ότι χρειάζονται πολύ περισσότερη ισχύ (σε πλάτος ταλάντωσης) για να παραχθούν,
ώστε να δώσουν την ίδια ακουστική αίσθηση στο ανθρώπινο αυτί και αυτό για δύο
λόγους:
1. Για να παραχθούν τα μπάσα χρειάζονται μεγάλες
επιφάνειες ή «χοντρές» χορδές. Αν συγκρίνει κανείς την ογκώδη κατασκευή ενός
ηχείου woofer (μπάσο) με την πολύ μικρότερη ενός tweeter (πρίμο),
ή μίας μπάσας χορδής με μία πρίμα, η διαφορά γίνεται εμφανής.
2. Το ανθρώπινο αυτί είναι πολύ πιο «αναίσθητο» στα μπάσα
απ’ ότι στα πρίμα, οπότε χρειάζεται πολύ μεγαλύτερο πλάτος ταλάντωσης από τις
μπάσες ηχητικές συσκευές σε σχέση με τις πρίμες, για να παραχθεί το ίδιο
ακουστικό αποτέλεσμα. Η αργή, μεγάλου πλάτους ταλάντωση του κώνου ενός woofer, είναι
χαρακτηριστική.
Από την άλλη πλευρά, τα μπάσα άπαξ και παραχθούν δεν
απορροφώνται εύκολα από τον αέρα, σε αντίθεση με τα πρίμα που απορροφώνται
πολύ περισσότερο. Επιπλέον τα μπάσα «παρακάμπτουν» εμπόδια, ενώ τα πρίμα
«σκοντάφτουν» επάνω τους και εξασθενούν. Γι’ αυτό από τις μακρινές βροντές
ακούμε μόνο το μπάσο του ήχου τους, τα ραδιοφωνικά κύματα τα λαμβάνουμε
πρακτικά παντού, ενώ τα τηλεοπτικά που είναι μεγαλύτερης συχνότητας χρειάζονται
«οπτική επαφή», όπως εξάλλου και το ίδιο το φως.
Μάλιστα τα όρια των οπτικών μικροσκοπίων προκύπτουν από
το γεγονός ότι το φως δεν εμποδίζεται αλλά παρακάμπτει τα αντικείμενα με μέγεθος μικρότερο από το μήκος κύματος του,
με αποτέλεσμα τα πολύ μικρά αντικείμενα να γίνονται αόρατα. Η μέθοδος λοιπόν που εφαρμόζεται για να
ξεπεράσουμε αυτό το πρόβλημα είναι να «φωτίσουμε» τα πολύ μικρά αυτά
αντικείμενα με ηλεκτρομαγνητικά κύματα ακόμα μικρότερου μήκους κύματος από το
φως, όπως οι ακτίνες Χ ή οι δέσμες ηλεκτρονίων.
67. Ταχύτητα
τροχιάς και ταχύτητα διαφυγής.
Συχνά γίνεται σύγχυση μεταξύ ταχύτητας τροχιάς και
ταχύτητας διαφυγής. Η ταχύτητα τροχιάς είναι η ταχύτητα που χρειάζεται ένα
διαστημόπλοιο για να παραμείνει σε τροχιά γύρω από ένα ουράνιο σώμα. συνήθως βέβαια
αναφερόμαστε στη Γη.
Ενώ η ταχύτητα διαφυγής είναι η αρχική ταχύτητα που
απαιτείται ώστε ένα διαστημόπλοιο να ξεφύγει από την έλξη ενός ουράνιου σώματος
και να κινηθεί στο διάστημα. Υπόψη ότι μιλάμε για αρχική ταχύτητα όπως στην
περίπτωση ενός βλήματος κανονιού (και χωρίς να ληφθεί υπόψη η αντίσταση της
ατμόσφαιρας) και όχι για την περίπτωση ενός πυραύλου όπου η ταχύτητα αυξάνεται
προοδευτικά, επειδή στη δεύτερη περίπτωση η απαιτούμενη τελική ταχύτητα
διαφυγής εξαρτάται από το ύψος που θα βρεθεί, όταν σταματήσει η προώθησή του.
Έτσι, ενώ η ταχύτητα διαφυγής είναι συγκεκριμένη (για τη
Γη είναι 11.2 km/s), η ταχύτητα τροχιάς εξαρτάται από το ύψος της. Για τη χαμηλότερη πρακτικά τροχιά, σε ύψος περίπου 350 km πάνω από
την επιφάνεια της Γης απαιτείται ταχύτητα 7.7 km/s*, ενώ όσο
η τροχιά γίνεται ψηλότερη η ταχύτητα αυτή μειώνεται. για παράδειγμα οι γεωστατικοί τηλεπικοινωνιακοί
δορυφόροι σε ύψος 36.000 km από την επιφάνεια της Γης κινούνται με ταχύτητα 3.3 km/s.
Επίσης για σύγκριση, η ταχύτητα διαφυγής από το Ηλιακό Σύστημα είναι περίπου 18 km/s, ενώ περιέργως, για να φθάσει ένα διαστημόπλοιο στον Ήλιο θα χρειάζονταν ακόμα μεγαλύτερη αρχική ταχύτητα! Και μάλιστα πολύ περισσότερη ενέργεια, αν συνυπολογίσουμε και το αναγκαίο "φρενάρισμα" στο τέλος.
Για την ιστορία, η ταχύτητα των Apollo** μειώνονταν μέχρι τα 2.2 km/s στο σημείο της διαδρομής προς τη Σελήνη όπου η βαρύτητα της τελευταίας άρχιζε να υπερτερεί, ενώ λίγο πριν την επανείσοδο στην τροχιά της Γης μετά την εκτέλεση της αποστολής, η ταχύτητα είχε ανέβει πάλι κοντά στην ταχύτητα διαφυγής. Υπόψην ότι οι ταχύτητες είχαν επιλεγεί έτσι ώστε η αποστολή να εκτελεστεί σε εύλογο χρονικό διάστημα, αλλά και με τη μικρότερη δαπάνη καυσίμων τόσο για την επιτάχυνση όσο και για την επιβράδυνση των διαστημοπλοίων.
*Θεωρητικά 8 km/s λίγο επάνω από την επιφάνεια της Γης, αν δεν υπήρχε η ατμόσφαιρα, καθώς η ταχύτητας διαφυγής σε οποιουδήποτε ουράνιο σώμα είναι ίση με την ταχύτητα χαμηλής τροχιάς επί την τετραγωνική ρίζα του 2.
**Η αρχική ταχύτητα (10.4 km/s) ήταν λίγο χαμηλότερη από την ταχύτητα διαφυγής, ώστε το διαστημόπλοιο να μπει σε μια πολύ ελλειπτική τροχιά (βλέπε και παρακάτω) που θα έφθανε μέχρι σ' ένα σημείο που υπερτερεί η βαρύτητα της Σελήνης.
Παρά τη μικρότερη ταχύτητα όμως, για την ψηλότερη τροχιά χρειάζεται περισσότερη συνολική ενέργεια (δηλαδή μεγαλύτερο πύραυλο), επειδή τα διαστημόπλοια θα πρέπει να μετακινηθούν σε μεγαλύτερη απόσταση ενάντια στη έλξη της βαρύτητας της Γης, κάτι που «μετράει» περισσότερο από τη μείωση της ταχύτητας. Στην ακραία περίπτωση, σε πολύ μεγάλη απόσταση από τη Γη, η ταχύτητα τροχιάς θα ήταν μηδενική, αφού ουσιαστικά ο δορυφόρος θα ήταν εκτός της βαρύτητας της Γης (κάτι που πρακτικά συμβαίνει 1.5 εκατομμύριο χιλιόμετρα από την επιφάνεια της Γης (σφαίρα του Hill, βλέπε και θέμα Νο 24).
Αν λοιπόν ένα διαστημόπλοιο βρεθεί με ταχύτητα μεγαλύτερη
της απαιτούμενης για τη δεδομένη τροχιά του (όπως αν ενεργοποιήσει τους
προωθητές του) αλλά μικρότερη της ταχύτητας διαφυγής, θα ανεβάσει το επίπεδο
της τροχιάς του χάνοντας ταυτόχρονα ταχύτητα, μέχρι να ισορροπήσει σε
μία νέα ψηλότερη τροχιά*. Αντίθετα αν στην τροχιά που βρίσκεται χάνει ταχύτητα
(κάτι που συμβαίνει βαθμιαία στους δορυφόρους χαμηλής τροχιάς, επειδή εκεί
υπάρχουν ακόμα μόρια της ατμόσφαιρας) το ύψος της τροχιάς θα μειώνεται με
ταυτόχρονη αύξηση της ταχύτητάς του, μέχρι να συναντήσει πυκνότερη ατμόσφαιρα (σε υψόμετρο περίπου 250 km), οπότε θα χάσει σχετικά απότομα σημαντική ενέργεια και ταχύτητα μέχρι τελικά να αναφλεγεί από την τριβή (ουσιαστικά από τη συμπίεση του αέρα)**. Αυτός είναι και ο τρόπος για να επιστρέψουν τα διαστημόπλοια στη Γη χωρίς να καούν (πολύ), "φρενάροντας" αρχικά την ταχύτητά τους με τους πυραυλοκινητήρες τους.
Φυσικά στα διαστημόπλοια που προορίζονται να κινηθούν στο
Διάστημα (εκτός τροχιάς γύρω από τη Γη) δίνεται ταχύτητα αρκετά μεγαλύτερη της ταχύτητας διαφυγής, ώστε να
«περισσέψει» και αρκετή για να εκτελέσουν την αποστολή τους σε εύλογο χρόνο.
*Αυτό δεν είναι τόσο απλό όσο ακούγεται, καθώς η αύξηση της ταχύτητας θα κάνει την κυκλική τροχιά αρχικά ελλειπτική. Το απόγειο της ελλειπτικής τροχιάς θα έχει υπολογιστεί να βρίσκεται στο ύψος της νέας τροχιάς. Καθώς λοιπόν το διαστημόπλοιο θα βρίσκεται στο απόγειο, μία ακόμα ενεργοποίηση των προωθητών του θα μετατρέψει την ελλειπτική τροχιά σε κυκλική, αλλά πλέον στο νέο υψόμετρο. Δεν είναι τυχαία η έκφραση "rocket science" για κάτι πολύ δυσνόητο! Η εικόνα κάτω δείχνει ακριβώς αυτή τη διαδικασία, που είναι γνωστή και σαν "μετάβαση Hohmann" (μαύρα βέλη). Παρόμοια, το χαμήλωμα σε κυκλική τροχιά γίνεται με δύο αντίστοιχα "φρεναρίσματα".
**Δηλαδή συμβαίνει το φαινομενικά παράδοξο, η αύξηση της αεροδυναμικής αντίστασης να οδηγεί (αρχικά) σε μικρή αύξηση της ταχύτητας του διαστημοπλοίου! Προφανώς η παροχή ενέργεια προέρχεται από τη μεταβολή του ύψους τροχιάς.
ΥΓ1. Η ταχύτητα διαφυγής είναι ένα σχετικά εύκολα υπολογίσιμο νούμερο. Όμως ένα άλλο θέμα είναι το πώς αναπτύσσεται αυτή η ταχύτητα. Εδώ υπάρχει ένας περιορισμός. Το βάρος ενός πυραύλου αποτελείται κυρίως από καύσιμο για να μπορέσει να αναπτύξει αυτήν την ταχύτητα. Όμως τα υγρά ή υγροποιημένα καύσιμα που χρησιμοποιούνται έχουν σημαντικό βάρος και αν η βαρύτητα της Γης ήταν 10% μεγαλύτερη, το επιπλέον καύσιμο που θα χρειάζονταν δεν θα επέτρεπε την ανάπτυξη ταχύτητας διαφυγής.
ΥΓ2. Ένα ενδιαφέρον και σχετικά απλό βίντεο για την αλλαγή τροχιών (στα Αγγλικά), είναι το παρακάτω: https://www.youtube.com/watch?v=bcvnfQlz1x4
68. Οι καμινάδες που
πέφτουν και οι μαύρες τρύπες.
Οι καμινάδες που πέφτουν (από τη βάση τους), σπάνε. Και
πού είναι το περίεργο θα πει κάποιος. Το θέμα είναι ότι σπάνε πριν
χτυπήσουν στο έδαφος. Ο λόγος είναι ότι καθώς πέφτει η καμινάδα, τα τμήματα τα
πιο απομακρυσμένα από τη βάση διαγράφουν στον ίδιο χρόνο μεγαλύτερο τόξο από τα
τμήματα τα κοντινότερα στη βάση της. Αυτό έχει σαν αποτέλεσμα τα πιο ψηλά
τμήματα να υφίστανται μεγαλύτερη επιτάχυνση από τα χαμηλότερα, με συνέπεια η
καμινάδα να δέχεται πλευρικές διατμητικές δυνάμεις που τη σπάνε πριν καν
αγγίξει στο έδαφος.
Και τι σχέση έχει αυτό με τη μαύρη τρύπα; Στη μαύρη
τρύπα, η βάθμωση της βαρύτητας (δηλαδή η διαφοροποίηση της ισχύος του βαρυτικού
πεδίου σε διαφορετικά σημεία) είναι τόσο ισχυρή, που ένας (άτυχος) αστροναύτης
που θα έφτανε μέχρι εκεί κυριολεκτικά θα διαρρηγνύονταν από τις άνισες δυνάμεις
που θα εφαρμόζονταν στο σώμα του (σαν συνέπεια των διαφορετικών τιμών της
επιτάχυνσης της βαρύτητας), κάτι ανάλογο δηλαδή με αυτό που συμβαίνει στην
καμινάδα.
Έτσι είναι φανερό, ότι ένας άνθρωπος θα μπορούσε να
αντέξει άνετα οσοδήποτε ισχυρή επιτάχυνση, με την προϋπόθεση ότι είναι βαρυτική
(δηλαδή ασκείται σε όλα τα άτομα του σώματός του) και είναι ομοιογενής. (Βλέπε και θέμα Νο 80).
69. Όταν δύο γάστρες πλοίου έχουν μικρότερη αντίσταση από μία.
Τα
τελευταία χρόνια, τα μεγάλα καταμαράν επικρατούν στις ακτοπλοϊκές μεταφορές
εξαιτίας της μεγαλύτερης ταχύτητάς τους. Βέβαια οι ιστιοπλόοι αυτό το γνώριζαν
από παλιά, ότι δηλαδή τα ιστιοπλοϊκά καταμαράν είναι ασυναγώνιστα σε ταχύτητα
σε σχέση με τα κλασικά σκάφη αντίστοιχου μεγέθους.
Σε
ορισμένες πλεύσεις μάλιστα, μπορούν να ξεπεράσουν σε ταχύτητα ακόμα και τον
αέρα που τα κινεί! (Βλ και θέμα Νο 64).
Η ταχύτητα των καταμαράν οφείλεται στο γεγονός ότι μια
γάστρα εκτοπίσματος (δηλαδή που δεν μειώνεται ο βυθισμένος όγκος της με την αύξηση της ταχύτητας, σε αντίθεση με τις γάστρες πλαναρίσματος των ταχύπλοων) έχει μια πρακτικά
μέγιστη ταχύτητα που εξαρτάται σημαντικά από τον λόγο μήκους προς το πλάτος
της.
Έτσι οι δύο γάστρες του καταμαράν εξαιτίας που πολύ «στενόμακρου» σχήματός τους, συνολικά έχουν μικρότερη αντίσταση από τη μοναδική γάστρα ενός κλασικού σκάφους ίσου μήκους.
70. Όταν οι πολλοί στρόβιλοι είναι καλύτεροι από τον έναν.
Έτσι οι δύο γάστρες του καταμαράν εξαιτίας που πολύ «στενόμακρου» σχήματός τους, συνολικά έχουν μικρότερη αντίσταση από τη μοναδική γάστρα ενός κλασικού σκάφους ίσου μήκους.
70. Όταν οι πολλοί στρόβιλοι είναι καλύτεροι από τον έναν.
Ο στροβιλισμός στα ρευστά (υγρά ή αέρια) σημαίνει
απώλειες και πρέπει να αποφεύγεται όσο είναι δυνατόν. Ο στροβιλισμός όμως
παράγεται αναπόφευκτα από την κίνηση ενός ρευστού σε επαφή με τα τοιχώματα ενός
αγωγού είτε από την κίνηση ενός σώματος μέσα στο ρευστό, εφόσον ξεπεραστεί μια
κρίσιμη ταχύτητα. Φυσικά το σχήμα του αντικειμένου έχει πολύ μεγάλη σημασία,
γι’ αυτό συνήθως τα σχήματα για κίνηση μέσα σε ρευστά είναι τα γνωστά
υδροδυναμικά ή αεροδυναμικά (όσο οι πρακτικοί περιορισμοί το επιτρέπουν), με
στόχο να καθυστερήσει όσο το δυνατόν η εμφάνιση στροβίλων, καθώς η ταχύτητα
αυξάνεται.
Υπάρχουν όμως και περιπτώσεις όπου επιδιώκεται η
δημιουργία πολλών μικρών στροβίλων ώστε να καθυστερήσει η εμφάνιση ενός
μεγαλύτερου, που θα προκαλούσε μεγαλύτερη αντίσταση στην κίνηση του σώματος, ή θα
δημιουργούσε κραδασμούς.
Τέτοια παραδείγματα είναι οι μικρές προεξοχές σε ορισμένα σημεία στις πτέρυγες κάποιων αεροσκαφών (vortex generators), η ελικοειδής ταινία γύρω από καμινάδες ή σωληνώσεις εκτεθειμένες σε δυνατό άνεμο, τα «λακκάκια» στα μπαλάκια του γκολφ (προέκυψαν από την παρατήρηση ότι τα «γραντζουνισμένα» μπαλάκια έφταναν μακρύτερα), και η επένδυση με μικροπροεξοχές σε γάστρες ιστιοπλοϊκών σκαφών και στολές κολυμβητών.
Τέτοια παραδείγματα είναι οι μικρές προεξοχές σε ορισμένα σημεία στις πτέρυγες κάποιων αεροσκαφών (vortex generators), η ελικοειδής ταινία γύρω από καμινάδες ή σωληνώσεις εκτεθειμένες σε δυνατό άνεμο, τα «λακκάκια» στα μπαλάκια του γκολφ (προέκυψαν από την παρατήρηση ότι τα «γραντζουνισμένα» μπαλάκια έφταναν μακρύτερα), και η επένδυση με μικροπροεξοχές σε γάστρες ιστιοπλοϊκών σκαφών και στολές κολυμβητών.
Μία άλλη εφαρμογή της ίδιας αρχής, ήταν στα αερόφρενα των παλιών (Β'ΠΠ) βομβαρδιστικών κάθετης εφόρμησης (εικόνα κάτω), που είχαν πολλές μεγάλες ή μικρότερες τρύπες. Τα αερόφρενα άνοιγαν για να μην αυξάνεται υπερβολικά η ταχύτητα κατά τη σχεδόν κάθετη βύθιση.
Όμως, ειδικά αν τα αερόφρενα ήταν μεγάλα, εάν δεν είχαν τις τρύπες θα δημιουργούσαν ένα ισχυρό στρόβιλο πίσω τους που θα καταπονούσε την κατασκευή με κραδασμούς και ταλαντώσεις, και επιπλέον ο στρόβιλος φτάνοντας μέχρι τα πτερύγια της ουράς θα μείωνε την ικανότητα διατήρησης σταθερής πορείας και σκόπευσης κατά τη βύθιση.
Οι τρύπες, δημιουργούσαν πολλούς μικρότερους στροβίλους που δεν μείωναν ουσιαστικά την ικανότητα "φρεναρίσματος", αλλά επειδή οι στρόβιλοι αυτοί ήταν τυχαίοι και όχι συγχρονισμένοι, οι εγκάρσιες δυνάμεις που ασκούσαν επάνω στο αερόφρενο (και κατά συνέπεια και επάνω στο αεροσκάφος) σε μεγάλο ποσοστό αλληλοεξουδετερόνονταν, και επίσης αποφεύγονταν η δημιουργία ενός μεγάλου στροβίλου που θα επηρέαζε την ουρά.
Είναι
γνωστό ότι το Σύμπαν είναι ηλικίας περίπου 14 δισεκατομμυρίων ετών. Ποιες είναι
όμως οι διαστάσεις του;
Εδώ θα
πρέπει να διευκρινίσουμε ότι μπορούμε να μιλάμε μόνο για το ορατό Σύμπαν,
δηλαδή μέχρι εκεί που μπορούμε να δούμε με τα ισχυρότερα οπτικά και ραδιο-τηλεσκόπιά μας (και να
κάνουμε και κάποιους υπολογισμούς, βλ παρακάτω).
Από τα
πιο απομακρυσμένα σημεία του Σύμπαντος (δηλαδή από τους πιο απομακρυσμένους
γαλαξίες), το φως που φτάνει σ’ εμάς ξεκίνησε να έρχεται πριν από 13,4 δισεκατομμύρια χρόνια, ενώ "λίγο" μακρύτερα στα 13.8 δισεκατομμύρια χρόνια, ανιχνεύθηκε η ακτινοβολία "υποβάθρου", κατάλοιπο της Μεγάλης Έκρηξης. Επειδή όμως το Σύμπαν συνεχώς διαστέλλεται και μάλιστα
επιταχυνόμενα (περισσότερα γι’ αυτό παρακάτω), οι γαλαξίες αυτοί έχουν στο
μεταξύ απομακρυνθεί πολύ περισσότερο, με αποτέλεσμα να υπολογίζεται ότι σήμερα βρίσκονται σε
απόσταση γύρω στα 46.5 δισεκατομμύρια έτη φωτός* από τη Γη, δίνοντας μία
διάμετρο** στο ορατό Σύμπαν (συνυπολογίζοντας και την στο μεταξύ διαστολή του)
γύρω στα 93 δισεκατομμύρια έτη φωτός.
Όμως δεν θα πρέπει να σκεφτούμε ότι η Γη βρίσκεται στο κέντρο του Σύμπαντος, αλλά θα πρέπει να φανταστούμε το Σύμπαν σαν ένα μπαλόνι που φουσκώνει (οι Άγγλοι χρησιμοποιούν το παράδειγμα της πουτίγκας με σταφίδες που φουσκώνει στον φούρνο, κάτι που δίνει και 3η διάσταση στο παράδειγμα) και τους γαλαξίες σαν σημάδια επάνω στην επιφάνειά του.
Όμως δεν θα πρέπει να σκεφτούμε ότι η Γη βρίσκεται στο κέντρο του Σύμπαντος, αλλά θα πρέπει να φανταστούμε το Σύμπαν σαν ένα μπαλόνι που φουσκώνει (οι Άγγλοι χρησιμοποιούν το παράδειγμα της πουτίγκας με σταφίδες που φουσκώνει στον φούρνο, κάτι που δίνει και 3η διάσταση στο παράδειγμα) και τους γαλαξίες σαν σημάδια επάνω στην επιφάνειά του.
Καθώς
λοιπόν οι διαστάσεις του μπαλονιού αυξάνονται, όλα τα σημεία απομακρύνονται
μεταξύ τους, αλλά απομακρύνονται και από οποιοδήποτε σημείο θα θελήσουμε να
θεωρήσουμε σαν κέντρο.
Όπως προαναφέρθηκε
όμως, η διαστολή αυτή είναι επιταχυνόμενη, με την έννοια ότι οι πιο
απομακρυσμένοι γαλαξίες απομακρύνονται ταχύτερα από τους κοντινότερους.
Αυτό
συμβαίνει επειδή κάθε γαλαξίας απομακρύνεται από τους γειτονικούς του με
περίπου την ίδια ταχύτητα, ας την ονομάσουμε α.
Οπότε,
όσο μακρύτερα βρίσκεται ένας γαλαξίας από εμάς (το συμβατικό κέντρο του
Σύμπαντος όπως προαναφέρθηκε), τόσοι περισσότεροι γαλαξίες παρεμβάλλονται, και
κάθε γαλαξίας απομακρύνεται με ταχύτητα α επί τον αριθμό των ενδιάμεσων γαλαξιών.
Τώρα το γιατί το Σύμπαν διαστέλλεται, έχει να κάνει με τεράστιες απωστικές δυνάμεις που δρουν επάνω στους γαλαξίες αντίθετα με τη βαρύτητα. Γι' αυτό η ενέργεια πίσω από αυτές τις δυνάμεις ονομάζεται "σκοτεινή ενέργεια" για να υποδηλώσει ακριβώς την άγνοιά μας σχετικά με τη φύση της.***
Τώρα το γιατί το Σύμπαν διαστέλλεται, έχει να κάνει με τεράστιες απωστικές δυνάμεις που δρουν επάνω στους γαλαξίες αντίθετα με τη βαρύτητα. Γι' αυτό η ενέργεια πίσω από αυτές τις δυνάμεις ονομάζεται "σκοτεινή ενέργεια" για να υποδηλώσει ακριβώς την άγνοιά μας σχετικά με τη φύση της.***
*Το έτος
φωτός είναι μήκος (η απόσταση που διατρέχει το φως σε ένα έτος).
**Θεωρώντας το συμβατικά σφαιρικό με κέντρο τη Γη, κάτι που φυσικά (ειδικά το δεύτερο) δεν ισχύει στην πραγματικότητα.
***Σε αντίθεση η "σκοτεινή ύλη", αν και εξίσου άγνωστη με τη "σκοτεινή ενέργεια", δρα όπως η βαρύτητα αλλά περιορίζει τη δράση της μέσα στους ίδιους τους γαλαξίες.
72. Ψυχρή συγκόλληση μετάλλων στο Διάστημα.
**Θεωρώντας το συμβατικά σφαιρικό με κέντρο τη Γη, κάτι που φυσικά (ειδικά το δεύτερο) δεν ισχύει στην πραγματικότητα.
***Σε αντίθεση η "σκοτεινή ύλη", αν και εξίσου άγνωστη με τη "σκοτεινή ενέργεια", δρα όπως η βαρύτητα αλλά περιορίζει τη δράση της μέσα στους ίδιους τους γαλαξίες.
72. Ψυχρή συγκόλληση μετάλλων στο Διάστημα.
Αν και στην πράξη το φαινόμενο αυτό είναι σπάνιο, καθώς θα πρέπει να συμπέσουν πολλές κατάλληλες συνθήκες (μάλλον ακατάλληλες, αφού το φαινόμενο είναι ανεπιθύμητο), στη θεωρία μπορεί να συμβεί, και σε μία τουλάχιστον περίπτωση μια δυσλειτουργία του συστήματος ξεδιπλώματος μιας κεραίας διαστημοπλοίου αποδόθηκε σ’ αυτό.
Πρόκειται για την αυτογενή συγκόλληση που μπορεί να συμβεί, αν δύο απόλυτα καθαρές και πολύ λείες επιφάνειες από το ίδιο μέταλλο έλθουν σε επαφή και πιεστούν μεταξύ τους με αρκετή δύναμη. Τότε τα άτομα στις δύο επιφάνειες προσεγγίζουν τόσο πολύ μεταξύ τους, που αποκτούν «συνέχεια», συμπεριφέρονται δηλαδή πια σαν να πρόκειται για ενιαίο υλικό. Ο χώρος του Διαστήματος εξασφαλίζει την προϋπόθεση της απόλυτης καθαρότητας, καθώς οι δύο επιφάνειες θα πρέπει να είναι απαλλαγμένες από κάθε ίχνος υλικού ξένου προς το καθαρό μέταλλο και βέβαια όλα τα μέταλλα στη Γη αναπτύσσουν ταχύτατα ένα αόρατο επιφανειακό στρώμα οξείδωσης.
Προφανώς, για να συμβεί η ψυχρή συγκόλληση στο Διάστημα τα υλικά θα πρέπει να καθαριστούν αφού μεταφερθούν στο Διάστημα και αφού προηγουμένως (στη Γη) έχουν υποστεί κατεργασία ώστε να αποκτήσουν τελείως επίπεδες και λείες επιφάνειες. Επιπλέον, θα πρέπει να εξασφαλιστεί ότι οι κρύσταλλοι των μετάλλων στην επιφάνεια επαφής θα έχουν τον ίδιο προσανατολισμό. Από τα παραπάνω, είναι φανερό ότι το πρόβλημα είναι περισσότερο θεωρητικό παρά ουσιαστικό, αλλά όταν ρισκάρονται εκατομμύρια δολάρια σε μια διαστημική αποστολή και ίσως και ανθρώπινες ζωές, τίποτα δεν πρέπει να αφήνεται στην τύχη του.
73. Πηγή τάσης και πηγή ρεύματος.
Πρόκειται για την αυτογενή συγκόλληση που μπορεί να συμβεί, αν δύο απόλυτα καθαρές και πολύ λείες επιφάνειες από το ίδιο μέταλλο έλθουν σε επαφή και πιεστούν μεταξύ τους με αρκετή δύναμη. Τότε τα άτομα στις δύο επιφάνειες προσεγγίζουν τόσο πολύ μεταξύ τους, που αποκτούν «συνέχεια», συμπεριφέρονται δηλαδή πια σαν να πρόκειται για ενιαίο υλικό. Ο χώρος του Διαστήματος εξασφαλίζει την προϋπόθεση της απόλυτης καθαρότητας, καθώς οι δύο επιφάνειες θα πρέπει να είναι απαλλαγμένες από κάθε ίχνος υλικού ξένου προς το καθαρό μέταλλο και βέβαια όλα τα μέταλλα στη Γη αναπτύσσουν ταχύτατα ένα αόρατο επιφανειακό στρώμα οξείδωσης.
Προφανώς, για να συμβεί η ψυχρή συγκόλληση στο Διάστημα τα υλικά θα πρέπει να καθαριστούν αφού μεταφερθούν στο Διάστημα και αφού προηγουμένως (στη Γη) έχουν υποστεί κατεργασία ώστε να αποκτήσουν τελείως επίπεδες και λείες επιφάνειες. Επιπλέον, θα πρέπει να εξασφαλιστεί ότι οι κρύσταλλοι των μετάλλων στην επιφάνεια επαφής θα έχουν τον ίδιο προσανατολισμό. Από τα παραπάνω, είναι φανερό ότι το πρόβλημα είναι περισσότερο θεωρητικό παρά ουσιαστικό, αλλά όταν ρισκάρονται εκατομμύρια δολάρια σε μια διαστημική αποστολή και ίσως και ανθρώπινες ζωές, τίποτα δεν πρέπει να αφήνεται στην τύχη του.
73. Πηγή τάσης και πηγή ρεύματος.
Μία πηγή
τάσης είναι η συνηθισμένη μπαταρία και επίσης το οικιακό δίκτυο του ηλεκτρικού
ρεύματος. Σε μία πηγή τάσης, η ένταση που θα διατρέξει το κύκλωμα εξαρτάται από
τη συνολική αντίσταση που παρεμβάλλεται στο κύκλωμα, σύμφωνα με τον πολύ γνωστό
τύπο του νόμου του Ωμ: I = V / R.
Υπάρχει όμως
και η πηγή ρεύματος, πολύ λιγότερο συνηθισμένη, όπου η ένταση του ρεύματος δεν
εξαρτάται πρακτικά από το φορτίο, η πτώση τάσης στα άκρα του όμως δίνεται πάλι
από τον νόμο του Ωμ: V = I X R.
Ένα
παράδειγμα πηγής ρεύματος είναι οι μετασχηματιστές μέτρησης έντασης, στην ουσία μετασχηματιστές πολύ μικρής ισχύος που στο
πρωτεύον τους έχουν μόνον μερικές σπείρες ή και μόνο μία (στην τελευταία
περίπτωση αυτό σημαίνει μια τρύπα από την οποία διέρχεται το καλώδιο του προς μέτρηση
κυκλώματος), αλλά πάρα πολλές σπείρες στο δευτερεύον.
Το
ενδιαφέρον είναι ότι τα χαρακτηριστικά της πηγής ρεύματος είναι «ανάποδα» σε
σχέση με αυτά της πηγής τάσης. Δηλαδή ενώ η πηγή τάσης κινδυνεύει να
καταστραφεί από υπερένταση όταν βραχυκυκλώσουμε την έξοδό της (ή το δευτερεύον
κύκλωμα στην περίπτωση ενός μετασχηματιστή τάσης), ένας μετασχηματιστής έντασης κινδυνεύει να
καταστραφεί από υπέρταση όταν τα άκρα του δευτερεύοντος μείνουν ανοικτά. Γι’
αυτό τα άκρα του δευτερεύοντος σ’ έναν μετασχηματιστή έντασης πρέπει να
βραχυκυκλώνονται, όταν δεν υπάρχει κάποιο όργανο συνδεδεμένο σ’ αυτά.
Άλλο
χαρακτηριστικό είναι ότι η μια πηγής τάσης είναι τόσο καλύτερη όσο μικρότερη
είναι η εσωτερική της αντίσταση, το αντίθετο (δηλαδή όσο μεγαλύτερη είναι η
εσωτερική της αντίσταση) ισχύει για την πηγή έντασης.
Πάντως υπάρχει μία τουλάχιστον περίπτωση που θέλουμε μία πηγή τάσης να αντέχει και σε βραχυκύκλωμα και αυτή είναι η κλασική μηχανή ηλεκτροσυγκόλλησης, που αποκτά όμως αυτό το χαρακτηριστικό με ειδική σχεδίαση του πυρήνα του μετασχηματιστή της ώστε να αποκτήσει μεγάλη επαγωγική αντίσταση.
74. To μαύρο ταιριάζει στα ψυγεία και στα καλοριφέρ.
Πάντως υπάρχει μία τουλάχιστον περίπτωση που θέλουμε μία πηγή τάσης να αντέχει και σε βραχυκύκλωμα και αυτή είναι η κλασική μηχανή ηλεκτροσυγκόλλησης, που αποκτά όμως αυτό το χαρακτηριστικό με ειδική σχεδίαση του πυρήνα του μετασχηματιστή της ώστε να αποκτήσει μεγάλη επαγωγική αντίσταση.
74. To μαύρο ταιριάζει στα ψυγεία και στα καλοριφέρ.
Όχι στα
ψυγεία που έχουμε στην κουζίνα, αλλά στις μεταλλικές επιφάνειες που χρησιμοποιούμε
για να ακτινοβολούν θερμότητα. Φυσικά ή έννοια «ψυγείο» ή «θερμαντικό σώμα»
έχει σχέση με την κατεύθυνση που ρέει η θερμότητα ως προς το σημείο που μας ενδιαφέρει.
Για παράδειγμα, ένα ψυγείο αυτοκινήτου
μεταφέρει θερμότητα από το νερό της μηχανής στην ατμόσφαιρα, ενώ το θερμαντικό
σώμα του καλοριφέρ του αυτοκινήτου, ίδιο κατά τα άλλα με το ψυγείο της μηχανής
(εκτός από το μέγεθος), μεταφέρει θερμότητα από τη μηχανή στην καμπίνα του
αυτοκινήτου.
Η μεταφορά θερμότητας από τα ψυγεία στον αέρα, γίνεται με δύο τρόπους: Με μεταφορά (εξαιτίας της επαφής της θερμής επιφάνειας με τα μόρια του αέρα), και με ακτινοβολία. Ειδικά ο δεύτερος τρόπος επηρεάζεται από το χρώμα της πλευράς που ακτινοβολεί (προς τον αέρα), και όσο πιο σκούρα είναι τόσο περισσότερο ακτινοβολεί. Έτσι, το καλύτερο χρώμα για τη μετάδοση θερμότητας προς τον αέρα είναι το μαύρο και ειδικά το ματ. Προφανώς, δεν είναι καλή ιδέα να βάψουμε μαύρα τα σώματα του καλοριφέρ στο σπίτι για να βελτιώσουμε τη θερμική τους απόδοση, αλλά όπου δεν τίθεται θέμα αισθητικής αυτή είναι η καλύτερη λύση (υπάρχουν βέβαια και οι "προχωρημένες" διακοσμητικές λύσεις, όπως της εικόνας). Από την άλλη μεριά, το στρώμα της μπογιάς πρέπει να είναι όσο το δυνατόν λεπτότερο, ώστε να μην χάσουμε το πλεονέκτημα του σκούρου χρώματος, από τις (αναπόφευκτες) θερμικές μονωτικές ιδιότητες της μπογιάς.
Η μεταφορά θερμότητας από τα ψυγεία στον αέρα, γίνεται με δύο τρόπους: Με μεταφορά (εξαιτίας της επαφής της θερμής επιφάνειας με τα μόρια του αέρα), και με ακτινοβολία. Ειδικά ο δεύτερος τρόπος επηρεάζεται από το χρώμα της πλευράς που ακτινοβολεί (προς τον αέρα), και όσο πιο σκούρα είναι τόσο περισσότερο ακτινοβολεί. Έτσι, το καλύτερο χρώμα για τη μετάδοση θερμότητας προς τον αέρα είναι το μαύρο και ειδικά το ματ. Προφανώς, δεν είναι καλή ιδέα να βάψουμε μαύρα τα σώματα του καλοριφέρ στο σπίτι για να βελτιώσουμε τη θερμική τους απόδοση, αλλά όπου δεν τίθεται θέμα αισθητικής αυτή είναι η καλύτερη λύση (υπάρχουν βέβαια και οι "προχωρημένες" διακοσμητικές λύσεις, όπως της εικόνας). Από την άλλη μεριά, το στρώμα της μπογιάς πρέπει να είναι όσο το δυνατόν λεπτότερο, ώστε να μην χάσουμε το πλεονέκτημα του σκούρου χρώματος, από τις (αναπόφευκτες) θερμικές μονωτικές ιδιότητες της μπογιάς.
Αντίστοιχα,
και αυτό γίνεται πιο εύκολα αντιληπτό, οι μαύρες ματ επιφάνειες θερμαίνονται περισσότερο,
ειδικά εκτεθειμένες στον ήλιο που τις θερμαίνει αποκλειστικά με ακτινοβολία, γι’
αυτό και η μόδα των μαύρων ματ αυτοκινήτων δεν είναι καλή ιδέα, τουλάχιστον
στην Ελλάδα.
ΥΓ Πρόσφατα (δεκαετία του 2020), έχουν αναπτυχθεί επικαλύψεις με χρήση συνήθως νανοτεχνολογίας, είτε πολύ αντανακλαστικές (πιο άσπρες από τις άσπρες!) για χρήση πχ σε βαφές αυτοκινήτου, είτε πολύ απορροφητικές (πιο μαύρες και από την κόλαση!). Μάλιστα η τεχνολογία αυτή έχει και εφαρμογή σε οικοδομικά υλικά που διατηρούνται σαφώς πιο ψυχρά από το περιβάλλον, επειδή εκπέμπουν την θερμική ακτινοβολία που δέχονται από τον ήλιο σε τέτοια ζώνη συχνοτήτων που διαπερνά εύκολα τον αέρα, τα σύννεφα και το διοξείδιο του άνθρακα (αυτό που δημιουργεί το φαινόμενο του θερμοκηπίου), και αντινοβολείται πίσω στο Διάστημα. Ενδιαφέρον σχετικό άρθρο: https://xaidarisimera.gr/kafsones/?unapproved=243367&moderation-hash=0218d1ee50296f12d5bb321de5e0bfe9#comment-243367
75. Η στροφορμή του/της πατινέρ.
Ένα από
τα (φαινομενικά) παράδοξα της Μηχανικής (ένα άλλο είναι η συμπεριφορά του γυροσκοπίου),
είναι τα φαινόμενα που προκύπτουν από την αρχή της διατήρησης της στροφορμής.
Το πιο γνωστό και εντυπωσιακό παράδειγμα έχει να κάνει με την ταχύτητα της επί
τόπου περιστροφή ενός πατινέρ στον πάγο, η οποία, από τη στιγμή που έχει δοθεί
η αρχική φόρα, μειώνεται όταν ο πατινέρ απλώσει τα χέρια ή το πόδι του, ή
σκύψει, ενώ αντίθετα (που είναι και το πιο εντυπωσιακό), επιταχύνεται αν
μαζέψει τα άκρα του και ανορθωθεί.
Φυσικά,
το αποτέλεσμα δικαιολογείται εύκολα από το θεώρημα διατήρησης της στροφορμής
(αντίστοιχο με αυτό της διατήρησης της ορμής, αλλά για την περιστροφή), υπάρχει
όμως ένας απλός τρόπος να καταλάβουμε καλύτερα το φυσικό φαινόμενο.
Ας φανταστούμε
ένα άτομο που κάθεται σ’ ένα περιστρεφόμενο σκαμπό χωρίς τριβές, και κρατά δύο
βαρείς (σε σχέση με το δικό του βάρος) αλτήρες, με τα χέρια του μαζεμένα.
Ας υποθέσουμε
τώρα, ότι καθώς περιστρέφεται με αρχικά σταθερή ταχύτητα, ανοίγει τα χέρια του.
Φυσικά γνωρίζουμε ότι η περιστροφή του θα επιβραδυνθεί. Για να καταλάβουμε όμως
πώς συνέβη αυτό (πέρα από τους μαθηματικούς τύπους), ας σκεφτούμε ότι ο κάθε
αλτήρας καθώς περιστρέφονταν κοντά στο σώμα του ατόμου είχε μία γραμμική ταχύτητα.
Καθώς το χέρι απλώνεται, ο αλτήρας εξαιτίας της αδράνειας, θέλει προφανώς να
διατηρήσει τη γραμμική του ταχύτητα. Η ίδια γραμμική ταχύτητα όμως σε
μεγαλύτερη διάμετρο, σημαίνει μικρότερη γωνιακή ταχύτητα, δηλαδή μικρότερη
ταχύτητα περιστροφής, και βέβαια μέσω του χεριού επηρεάζει όλο το
περιστρεφόμενο σύστημα.
Το
αντίστροφο φυσικά θα συμβεί, όταν ο αθλητής μαζέψει τα χέρια του.
Αντίστοιχο φαινόμενο προκαλεί τις καμπύλες τροχιές, που αποδίδονται στις δυνάμεις Coriolis (βλ και θέμα Νο 15).
Αντίστοιχο φαινόμενο προκαλεί τις καμπύλες τροχιές, που αποδίδονται στις δυνάμεις Coriolis (βλ και θέμα Νο 15).
76. Η χαμένη τέχνη του λογαριθμικού κανόνα.
Ο
λογαριθμικός κανόνας ήταν το «κομπιουτεράκι» για τους πολλαπλασιασμούς και
διαιρέσεις των μηχανικών, από τις αρχές του 17ου αιώνα που
εφευρέθηκε μέχρι τις αρχές της δεκαετίας του 1970, οπότε αντικαταστάθηκε
σταδιακά από τα ηλεκτρονικά κομπιουτεράκια.
Και
αναφέρουμε ειδικά τους μηχανικούς, επειδή οι υπολογισμοί τους συνήθως δεν
απαιτούν υψηλή ακρίβεια, κάτι που ο λογαριθμικός κανόνας δεν μπορεί να
προσφέρει, μια και στις μηχανικές εφαρμογές εφαρμόζονται σχεδόν πάντοτε και
σημαντικοί συντελεστές ασφαλείας.
Σαν
κατασκευή, ο κανόνας αποτελείται από δύο ολισθαίνοντα ξύλινα ή πλαστικά
τμήματα, που επάνω στο καθένα είναι χαραγμένοι οι αριθμοί από το 1 έως το 10 (και σε άλλη θέση από το 1 έως το 100), όπως περίπου σ’ ένα χάρακα αλλά με μια
σημαντική διαφορά. Οι αποστάσεις των αριθμών βρίσκονται σε λογαριθμική σχέση,
για παράδειγμα οι αριθμοί από το 1 έως το 10 δεν ισαπέχουν μεταξύ τους αλλά
μοιάζουν να «συμπιέζονται» όσο πλησιάζουν το 10. Αυτές που ισαπέχουν είναι οι
δυνάμεις του δέκα, δηλαδή οι αριθμοί 1, 10, 100, 1000 κλπ που οι δεκαδικοί τους
λογάριθμοι είναι αντίστοιχα 0, 1, 2, 3 κλπ.
Βάζοντας
λοιπόν τα δύο ολισθαίνοντα τμήματα του κανόνα έτσι ώστε οι αριθμοί που θέλουμε
να πολλαπλασιάσουμε να είναι ο ένας στη συνέχεια του άλλου (δηλαδή να
προστίθενται) και διαβάζοντας τη συνολική ένδειξη, έχουμε το αποτέλεσμα του
πολλαπλασιασμού τους, σύμφωνα με την αρχή: loga +
logb = log(ab).
77. Η Γη αδυνατίζει!
77. Η Γη αδυνατίζει!
Κατ’ αρχήν, είναι προφανές ότι δεν μπορούμε να μιλάμε για
«βάρος» στην περίπτωση της Γης, αλλά για μάζα. Η μάζα της Γης πράγματι
αυξάνεται κατά περίπου 50.000 τόνους υλικού που δέχεται από το Διάστημα κάθε
χρόνο, αλλά ταυτόχρονα χάνει μάζα. Και χάνει μάζα με δύο τρόπους:
1. Με την αργή πυρηνική διάσπαση ραδιενεργών υλικών στο
εσωτερικό της, τα οποία μάλιστα συνεισφέρουν σημαντικά στη θέρμανσή της (15
τόνους τον χρόνο).
2. Με τη διαφυγή αερίων από την εξώτερη ατμόσφαιρά της,
κυρίως υδρογόνου και λιγότερο ηλίου (95.000 τόνους και 1600 τόνους αντίστοιχα).
Είναι φανερό λοιπόν ότι το ισοζύγιο είναι αρνητικό, δηλαδή η μάζα της Γης μειώνεται κατά περίπου 45.000 τόνους κάθε χρόνο, το οποίο μοιάζει αρκετό για τα ανθρώπινα μέτρα, αλλά είναι πραγματικά ασήμαντο για τη Γη (σα να φεύγει μία μύγα από έναν ελέφαντα κάθε χρόνο).
Θα αναρωτηθεί όμως κάποιος τι γίνεται με όλες τις
δραστηριότητες που παράγουν θερμότητα, πχ τις καύσεις, και αν αυτή δεν είναι
ενέργεια που ένα μέρος της ακτινοβολείται στο διάστημα, άρα κάτι χάνεται. Δεν είναι
όμως έτσι, γιατί όταν συντέθηκαν τα υλικά που καίμε σήμερα, τα μόρια τους είχαν
συνδεθεί με ενέργεια που προήλθε κυρίως από τον ήλιο, οπότε με την καύση αυτή η
ενέργεια σύνδεσης αποδεσμεύεται και θερμαίνει κατ’ αρχήν την ατμόσφαιρα και στη
συνέχεια ακτινοβολείται πίσω στο Διάστημα.
78.
Ένας «μαγικός» συγχρονισμός.
Ήταν το 1665, και ο Ολλανδός Φυσικός C. Huygens βρίσκονταν καθηλωμένος στο κρεβάτι του εξαιτίας μιας
αδιαθεσίας, όταν παρατήρησε ότι δύο όμοια ρολόγια με εκκρεμές κρεμασμένα στον
απέναντι τοίχο και σε μικρή απόσταση μεταξύ τους, συγχρόνιζαν τις ταλαντώσεις
τους μετά από λίγο, ακόμα και αν ξεκινούσαν με διαφορά φάσης, ενώ στη συνέχεια
παρέμεναν συγχρονισμένα.
Δεν είναι περίεργο ότι ο Huygens ενδιαφέρθηκε γι’ αυτό το φαινόμενο, μια και ο ίδιος ήταν
ο εφευρέτης του ρολογιού με εκκρεμές, περίπου μια δεκαετία πριν.
Αυτό που είναι περίεργο, είναι ότι το φαινόμενο παρέμενε
ανεξήγητο επί 350 χρόνια, δηλαδή μέχρι το 2015, οπότε και δόθηκε η επιστημονική
του εξήγηση.
Πανομοιότυπα ρολόγια με εκκρεμές έχουν φυσικά την ίδια ακριβώς
συχνότητα (εφόσον είναι σωστά ρυθμισμένα), αλλά η κίνησή τους μπορεί να
βρίσκεται σε διαφορά φάσης, δηλαδή τα εκκρεμή τους να μην βρίσκονται ποτέ σε
αντίστοιχη θέση. Αυτό που παρατηρήθηκε λοιπόν, είναι ότι η κίνηση των εκκρεμών
δημιουργεί παλμούς στον αέρα, και καθώς οι παλμοί αυτοί αλληλεπιδρούν
καταναλίσκουν ενέργεια. Παρόλο που η ενέργεια είναι ελάχιστη, ουσιαστικά
μηδενίζεται όταν οι κινήσεις των εκκρεμών συγχρονιστούν, οπότε τα εκκρεμή
τείνουν σε αυτή την ευσταθέστερη κατάσταση.
Μια πιο εμφανής επίδραση υπάρχει, όταν τα εκκρεμή είναι
σταθερά συνδεδεμένα μεταξύ τους αλλά βρίσκονται επάνω σε κινούμενο υπόβαθρο (εικόνα),
οπότε εκεί ο συγχρονισμός τους γίνεται μέσω της τάσης ελαχιστοποίησης του
κίνησης του υποβάθρου, καθώς η ενέργεια που εξοικονομείται με αυτό τον τρόπο
είναι μεγαλύτερη. Μια ενδιαφέρουσα επίδειξη αυτού του τελευταίου φαινομένου
βρίσκεται στο https://www.youtube.com/watch?v=T58lGKREubo
79. Το ψυγείο που «εξαφανίστηκε».
Όταν,
λίγο πριν τον 2ο παγκόσμιο πόλεμο η ισχύς των αεροπορικών κινητήρων
αυξάνονταν ραγδαία (φθάνοντας τελικά τους 1000 ίππους στην αρχή του πολέμου και τους 2500 ίππους προς το τέλος του), δημιουργήθηκε πρόβλημα
με την ψύξη τους. Στους βενζινοκινητήρες, τα 2/3 της ενέργειας του καυσίμου
μετατρέπονται κατ’ ευθείαν σε θερμότητα και μόνο το 1/3 σε ωφέλιμο έργο (πριν
και αυτό με τη σειρά του να μετατραπεί σε θερμότητα). Η μέχρι τότε μέθοδος
ψύξης κατ’ ευθείαν με αέρα δεν θα ήταν πλέον επαρκής χωρίς να αυξηθεί σημαντικά
η μετωπική τους επιφάνεια, πράγμα που θα επιδρούσε πολύ αρνητικά στις επιδόσεις ειδικά των καταδιωκτικών αεροσκαφών. Η λύση ήταν η υδρόψυξη, που επέτρεπε την κατασκευή κινητήρων με
πολύ μικρή μετωπική επιφάνεια, αλλά και αυτή δεν ήταν χωρίς προβλήματα, καθώς
τα ψυγεία, εκτεθειμένα στη ροή του αέρα, παρουσίαζαν και αυτά αρκετή αντίσταση.
Η λύση δόθηκε κατά τη διάρκεια του πολέμου, και αν και Βρετανικής έμπνευσης,
εφαρμόστηκε στην πληρέστερη μορφή της στο αμερικανικό καταδιωκτικό P-51 Mustang.
Το
ψυγείο εγκαταστάθηκε στο βάθος ενός μακρού αυλού εισαγωγής, που αρχικά αύξανε
τη διατομή του, και μετά το ψυγείο τη μείωνε. Η ιδέα ήταν ότι θερμότητα που
προσέδιδε το ψυγείο στον αέρα αύξανε την ταχύτητά του μετά απ’ αυτό, έτσι ώστε
να παράγεται ώθηση που αντιστάθμιζε και πρακτικά «εξαφάνιζε» την αεροδυναμική του
αντίσταση. Για να είναι αποτελεσματικό το φαινόμενο, ο αέρας κατά την
εισαγωγή του έπρεπε να συμπιεστεί, και αυτό επιτυγχάνονταν με την προοδευτική
αύξηση της διατομής του αυλού εισαγωγής, καθώς η μείωση της ταχύτητας προκαλεί
αύξηση της στατικής πίεσης. Επάνω στην ίδια αρχή βασίζονται και οι κινητήρες jet, μόνο που εκεί τη θερμότητα την προσφέρει το
καύσιμο και την αρχική συμπίεση τη δημιουργεί ένας αξονικός συμπιεστής.
80. Πώς ο άνθρωπος θα μπορούσε να αντέξει απεριόριστα g.
Είναι γνωστό ότι η αντοχή του ανθρώπου σε g (πολλαπλάσια της επιτάχυνσης της βαρύτητας) είναι μάλλον περιορισμένη και
εξαρτάται από τη διεύθυνση στην οποία εφαρμόζονται σε σχέση με το σώμα του, αλλά
και από τη διάρκειά τους (εικόνα). Γι’ αυτό οι πιλότοι και οι αστροναύτες έχουν μια κατά
το δυνατόν «ξαπλωτή» θέση, καθώς έτσι η
αντοχή τους στα g γίνεται μέγιστη, και με διάφορα "τρικ" και βοηθήματα φτάνουν σχεδόν τα 10g. Υπάρχουν τα θετικά g που «αδειάζουν» τον εγκέφαλο από το αίμα και τα αρνητικά που το συσσωρεύουν
εκεί. Τα δεύτερα είναι πολύ πιο επικίνδυνα (μπορεί να σπάσουν αιμοφόρα αγγεία
στον εγκέφαλο) οπότε και αντοχή του ανθρώπου σ’ αυτά είναι αρκετά μειωμένη.
Αλλά και η «δομική» αντοχή του ανθρώπου στα g είναι περιορισμένη, φθάνοντας μόνον τις μερικές δεκάδες g.
Κατόπιν αυτών, το ερώτημα του τίτλου
φαίνεται παράλογο, αλλά θα πρέπει να σκεφθούμε τι είναι αυτό που προκαλεί τα
προβλήματα στα πολλά g. Και αυτό είναι, το γεγονός ότι η
επιτάχυνση εφαρμόζεται στο εξωτερικό του σώματος του ανθρώπου, συνήθως στη
ράχη, ενώ η αδράνεια του σώματος ουσιαστικά το συνθλίβει επάνω στη ράχη και με τη σειρά τους
και τα εσωτερικά όργανα συνθλίβονται επάνω στη ράχη, από την εσωτερική πλευρά
φυσικά.
Αν όμως η επιτάχυνση είναι αποτέλεσμα βαρυτικού πεδίου* χωρίς το σώμα να στηρίζεται κάπου (όπως πχ στην ελεύθερη πτώση), όλα τα μέρη του σώματος, όλα τα μόρια του κλπ επιταχύνονται το ίδιο και δεν υπάρχουν δυνάμεις μεταξύ τους. Μάλιστα εφόσον η επιτάχυνση είναι βαρυτική, όσο μεγάλη και να είναι θα γίνεται αισθητή στον άνθρωπο σαν μία κατάσταση έλλειψης βαρύτητας! Ακόμα και σε μαύρη τρύπα να πέσει, θα ισχύει το ίδιο, με μια όμως προϋπόθεση. Το βαρυτικό πεδίο θα πρέπει να είναι ομοιογενές στις διαστάσεις του ανθρώπινου σώματος, αλλιώς η βάθμωσή του θα δημιουργήσει σημαντικές δυνάμεις επάνω στο σώμα.
Αν όμως η επιτάχυνση είναι αποτέλεσμα βαρυτικού πεδίου* χωρίς το σώμα να στηρίζεται κάπου (όπως πχ στην ελεύθερη πτώση), όλα τα μέρη του σώματος, όλα τα μόρια του κλπ επιταχύνονται το ίδιο και δεν υπάρχουν δυνάμεις μεταξύ τους. Μάλιστα εφόσον η επιτάχυνση είναι βαρυτική, όσο μεγάλη και να είναι θα γίνεται αισθητή στον άνθρωπο σαν μία κατάσταση έλλειψης βαρύτητας! Ακόμα και σε μαύρη τρύπα να πέσει, θα ισχύει το ίδιο, με μια όμως προϋπόθεση. Το βαρυτικό πεδίο θα πρέπει να είναι ομοιογενές στις διαστάσεις του ανθρώπινου σώματος, αλλιώς η βάθμωσή του θα δημιουργήσει σημαντικές δυνάμεις επάνω στο σώμα.
*Η άποψη αυτή είχε διατυπωθεί σε ραδιοφωνική συνέντευξη το 1966 από τον καθηγητή του Πολυτεχνείου Π. Σαντορίνη, ο οποίος έκανε την υπόθεση ότι τα ΑΤΙΑ (UFOs) ενδεχομένως χρησιμοποιούσαν κάποια μορφή αντιβαρύτητας για να κινηθούν με πολύ υψηλές επιταχύνσεις, μια άποψη που είχε διατυπώσει μία δεκαετία νωρίτερα ο αξιωματικός της γαλλικής αεροπορίας Jean Plantier.
81. Tα φωτόσπαθα των Jedi και η ατμοσφαιρική ρύπανση.
Όλοι λίγο πολύ γνωρίζουν τι είναι ένα
φωτόσπαθο Jedi, από τη γνωστή σειρά επιστημονικής φαντασίας «Πόλεμος των Άστρων». Όμως, αν θα θέλαμε να αφήσουμε για λίγο στην άκρη
τη «φαντασία» και να ασχοληθούμε με το «επιστημονικό» κομμάτι, έχουμε δύο
μεγάλα προβλήματα. Το πρώτο είναι ότι η δέσμη του φωτόσπαθου, το οποίο
υποτίθεται ότι είναι ένα ισχυρό laser, σταματάει απότομα
στο μήκος περίπου ενός κλασικού σπαθιού, και το δεύτερο είναι ότι ένα φωτόσπαθο
μπορεί να σταματήσει ένα άλλο όταν «διασταυρωθούν», επίσης όπως συμβαίνει με τα
κλασικά σπαθιά.
Φυσικά υποτίθεται ότι υπάρχει ιδιαίτερα
εξελιγμένη τεχνολογία την εποχή εκείνη (παρόλο που οι Jedi επιμένουν να τη
χρησιμοποιούν στη μορφή ενός μεσαιωνικού όπλου), αλλά ενώ μια τέτοια τεχνολογία
θα μπορούσε να δικαιολογήσει για παράδειγμα την ύπαρξη μιας πολύ ισχυρής πηγής
ενέργειας μέσα στη λαβή του φωτόσπαθου, δεν θα μπορούσε να ανατρέψει τις
βασικές ιδιότητες των laser.
Μία δέσμη laser λοιπόν δεν μπορεί να
σταματάει απότομα, εκτός και αν πέσει επάνω σ’ ένα αδιαφανές αντικείμενο που θα
τη διακόψει. Ή μήπως μπορεί;
Ένα τέτοιο φαινόμενο, δηλαδή απότομο
σταμάτημα μιας ακτίνας laser στο κενό, παρατηρείται όταν στρέψουμε ένα ισχυρό laser (όπως ένα πράσινο laser που χρησιμοποιείται για τη στόχευση αστεριών), προς
τον σκοτεινό ουρανό. Μερικές φορές, θα παρατηρήσουμε ότι η δέσμη του laser σταματάει σχετικά απότομα λίγες εκατοντάδες μέτρα επάνω από το σημείο που
βρισκόμαστε. Πώς είναι αυτό δυνατόν;
Κατ’ αρχήν, μία ακτίνα laser μέσα σε μία πολύ καθαρή ατμόσφαιρα, πχ σ’ ένα
δωμάτιο χωρίς σκόνη, δεν φαίνεται κατά τη διαδρομή της ενώ φαίνεται μόνο μία φωτεινή
κηλίδα όταν πέσει επάνω σ’ ένα αντικείμενο και αντανακλαστεί (ένα μέρος της)
επάνω του. Αν όμως υπάρχει σκόνη στον αέρα του δωματίου ή σταγονίδια συμπυκνωμένης υγρασίας, τότε η ακτίνα του laser θα διαγραφεί καθαρά. Η
ατμόσφαιρα στην ύπαιθρο, μέχρις ένα ορισμένο ύψος συνήθως μερικών εκατοντάδων
μέτρων, περιέχει αρκετά ξένα σωματίδια (στερεά ή συμπυκνώματα) που είναι γενικά
γνωστά σαν αεροζόλ. Αυτό το στρώμα του αεροζόλ σταματάει σχετικά απότομα σ’ ένα
ορισμένο ύψος από το έδαφος, ειδικά αν υπάρχει θερμοκρασιακή αναστροφή (όταν η
θερμοκρασία του αέρα αντί να συνεχίσει να μειώνεται με το ύψος όπως είναι το
φυσιολογικό, από κάποιο σημείο και μετά αρχίζει να ανεβαίνει).
Τότε το αεροζόλ παγιδεύεται σ’ ένα στρώμα κοντά
στο έδαφος, που αντανακλά έντονα τη δέσμη του laser που περνά από μέσα του,
ενώ πιο πάνω που η ατμόσφαιρα είναι καθαρή η ακτίνα του laser δεν φαίνεται, εκτός αν συναντήσει κάποιο χαμηλό σύννεφο, αεροπλάνο κλπ. Έτσι, μας δίνει την εντύπωση ότι η ακτίνα
σταματά απότομα, όμως αυτή η εξήγηση δεν μπορεί να χρησιμοποιηθεί για τα
φωτόσπαθα των Jedi. Ή
μήπως μπορεί;
82. Η "μαγική" πτήση του άλμπατρος.
Το άλμπατρος είναι ένα πολύ μεγάλο πουλί
(άνοιγμα φτερών 3.5 m) που ζει κυρίως στις νότιες θάλασσες. Ένα από τα χαρακτηριστικά που το κάνουν
ιδιαίτερο, πέρα από το ότι διαθέτει ιδανικό σχήμα για ανεμοπορία, είναι και ο τρόπος που πετάει καθώς μπορεί να παραμένει
στον αέρα για ημέρες, καλύπτοντας χιλιάδες
χιλιομέτρων χωρίς να κινεί ουσιαστικά
τα φτερά του, εξοικονομώντας με τον τρόπο αυτό σημαντική ενέργεια . Μάλιστα
πρόσφατα βρέθηκε ότι στη θέση έκτασης των φτερών,
το άλμπατρος μπορεί κατά κάποιο τρόπο να τα «κλειδώνει» εξοικονομώντας
ακόμα περισσότερη ενέργεια.
Είναι γνωστό ότι τόσο τα πουλιά όσο και οι
ανεμοπόροι μπορούν να κερδίζουν ύψος και να μένουν πολλές ώρες στον αέρα χωρίς
να δαπανούν ενέργεια προώθησης, εκμεταλλευόμενοι τα ανοδικά ρεύματα του αέρα
που είναι είτε θερμικά, όταν ο αέρας θερμαίνεται και ανεβαίνει, είτε δυναμικά
πλαγιάς, όταν προκαλούνται από πλαγιές που αναγκάζουν τον άνεμο να κινηθεί προς
τα επάνω.
Στον ανοικτό ωκεανό όμως δεν ισχύει τίποτα
από αυτά τα δύο, και παρότι σε γενικές γραμμές το πώς πετάει το άλμπατρος είναι
γνωστό από το τέλος του 19ου αιώνα, πρόσφατα με την τοποθέτηση επάνω σε πουλιά πομπών GPS, έγιναν γνωστές περισσότερες λεπτομέρειες.
Το άλμπατρος ενστικτωδώς εκμεταλλεύεται τη
βάθμωση της ταχύτητας του ανέμου (ή διάτμηση του ανέμου), δηλαδή το ότι η ταχύτητα του ανέμου είναι
πολύ χαμηλή κοντά στη επιφάνεια της θάλασσας εξαιτίας της τριβής με το νερό, ενώ
αυξάνεται με το ύψος.
Τα άλμπατρος λοιπόν κινούνται σε μία
διαδρομή «σλάλομ» γενικά κάθετα στην κατεύθυνση του ανέμου, στρίβοντας προς τον
άνεμο και αυξάνοντας το ύψος τους μέχρι το σημείο που η ταχύτητα του ανέμου δεν
αυξάνεται πια σημαντικά (10-20m) και μετά στρίβουν
και απομακρύνονται από τον άνεμο κατεβαίνοντας, αυξάνοντας με αυτόν τον τρόπο
την ταχύτητά τους. Αυτό το κάνουν συνεχόμενα με μία ομαλή κυματοειδή κίνηση, τόσο
στο οριζόντιο όσο και στο κατακόρυφο επίπεδο.
Η στροφή προς τον άνεμο αυξάνει τη δυναμική τους ενέργεια, δηλαδή το ύψος τους, ενώ η στροφή αντίθετα από τον άνεμο και το χαμήλωμα μετατρέπει την δυναμική ενέργεια σε κινητική. Επειδή αναπόφευκτα υπάρχουν απώλειες ενέργειας, το άλμπατρος τις αντισταθμίζει καθώς αφήνει να παρασύρεται λίγο από τον άνεμο, έτσι ώστε το ίχνος της διαδρομής (ως προς ένα σταθερό σημείο) που κάνει κινούμενο αντίθετα στον άνεμο να είναι λίγο μικρότερη από το ίχνος της διαδρομής που κάνει κινούμενο προς την κατεύθυνση του ανέμου. Ένα σύντομο και ενδιαφέρον βίντεο (στα αγγλικά) για την πτήση του άλμπατρος βρίσκεται στο: https://www.youtube.com/watch?v=uMX2wCJga8g
Η στροφή προς τον άνεμο αυξάνει τη δυναμική τους ενέργεια, δηλαδή το ύψος τους, ενώ η στροφή αντίθετα από τον άνεμο και το χαμήλωμα μετατρέπει την δυναμική ενέργεια σε κινητική. Επειδή αναπόφευκτα υπάρχουν απώλειες ενέργειας, το άλμπατρος τις αντισταθμίζει καθώς αφήνει να παρασύρεται λίγο από τον άνεμο, έτσι ώστε το ίχνος της διαδρομής (ως προς ένα σταθερό σημείο) που κάνει κινούμενο αντίθετα στον άνεμο να είναι λίγο μικρότερη από το ίχνος της διαδρομής που κάνει κινούμενο προς την κατεύθυνση του ανέμου. Ένα σύντομο και ενδιαφέρον βίντεο (στα αγγλικά) για την πτήση του άλμπατρος βρίσκεται στο: https://www.youtube.com/watch?v=uMX2wCJga8g
83. Τα θανάσιμα όμοια τρίγωνα.
Στη ναυσιπλοΐα όπως και στην αεροπλοΐα,
υπάρχει ένα ρητό που λέει ότι «τα όμοια τρίγωνα σκοτώνουν».
Αυτό προέρχεται από το γεγονός ότι εάν δύο
σκάφη ή αεροσκάφη που κινούνται με σταθερές ταχύτητες και σε ευθύγραμμες πορείες
βρίσκονται σε πορεία σύγκρουσης, σε οποιαδήποτε χρονική στιγμή οι θέσεις των
δύο σκαφών με το σημείο σύγκρουσης σχηματίζουν όμοια τρίγωνα. Αυτό σημαίνει,
ότι η διόπτευση του ενός σκάφους από τα άλλο είναι σε σταθερή γωνία. Δηλαδή από
τη θέση του πηδαλιούχου ή του πιλότου του κάθε σκάφους, η θέση του άλλου
βρίσκεται σταθερά στο ίδιο σημείο του παράθυρού του. Η μόνη αλλαγή είναι στο
μέγεθός του, που φυσικά αυξάνεται καθώς τα δύο σκάφη πλησιάζουν μεταξύ τους.
Όμως, επειδή το ανθρώπινο μάτι είναι κυρίως ευαίσθητο στην κίνηση, το άλλο
σκάφος μπορεί να περάσει απαρατήρητο, ειδικά αν η ορατότητα δεν είναι πολύ
καλή.
Υπάρχει όμως και ένα χειρότερο σενάριο,
στο οποίο μάλιστα αποδίδεται και μία αεροπορική τραγωδία σύγκρουσης μεταξύ
επιβατικών αεροσκαφών, που συνέβη αρκετές δεκαετίες πριν.
Μπορεί δηλαδή να τύχει, η θέση του άλλου
σκάφους να κρύβεται από το πλαίσιο που υπάρχει μεταξύ δύο παράθυρων, οπότε το
άλλο σκάφος θα κρύβεται συνεχώς και για μεγάλο διάστημα, τουλάχιστον μέχρι οι
διαστάσεις του να μεγαλώσουν αρκετά εξαιτίας της προσέγγισης, ώστε να φανεί
πίσω από το πλαίσιο.
Ειδικά όμως για τα αεροσκάφη που κινούνται με πολύ μεγάλες ταχύτητες, ο χρόνος αντίδρασης που μένει στον πιλότο είναι πλέον μηδαμινός για οποιονδήποτε ελιγμό αποφυγής.
Ειδικά όμως για τα αεροσκάφη που κινούνται με πολύ μεγάλες ταχύτητες, ο χρόνος αντίδρασης που μένει στον πιλότο είναι πλέον μηδαμινός για οποιονδήποτε ελιγμό αποφυγής.
84. Stealth (απόκρυψη) εναντίον αεροδυναμικής.
Το σχήμα των stealth αεροσκαφών είναι πλέον πολύ γνωστό, αλλά δεν παύει να είναι περίεργο.
Αρχικά εντύπωση προκαλούν οι επίπεδες επιφάνειες, που όπως είναι γνωστό
αντανακλούν με τον καλύτερο τρόπο την προσπίπτουσα ακτινοβολία, κάτι που
προφανώς ένα stealth αεροσκάφος προσπαθεί με κάθε τρόπο να αποφύγει.
Όμως αυτό που έχει σημασία δεν είναι
γενικά η αντανάκλαση, αλλά το να μην επιστρέφει η αντανάκλαση πίσω στο ραντάρ,
καθώς σχεδόν πάντα η ίδια κεραία παίζει τον ρόλο και του πομπού και του δέκτη
(με ταχύτατη εναλλαγή ρόλων μεταξύ τους).
Μια καμπύλη ή σφαιρική επιφάνεια, όπως
αυτή ενός παραδοσιακού αεροσκάφους , θα παρουσιάζει πάντα μια μικρή επιφάνεια που θα είναι κάθετη
στην εισερχόμενη ακτινοβολία του ραντάρ, άρα θα στέλνει ένα μικρό μέρος της κατ’
ευθείαν πίσω. Μια επίπεδη επιφάνεια όμως, ανάλογα με την κλίση της μπορεί να
κατευθύνει όλη την ακτινοβολία μακριά από την
πηγή της. Γι’ αυτό αποφεύγονται οι κατακόρυφες επίπεδες επιφάνειες (πχ
σε stealth πλοία) οι οποίες έχουν συνήθως κλίση προς το κέντρο, ώστε την ακτινοβολία
που έρχεται από χαμηλότερα ή από το ίδιο ύψος να την αντανακλούν προς τα επάνω.
Για αντίστοιχο λόγο, οι γυάλινες επιφάνειες του πιλοτηρίου των επιθετικών
ελικοπτέρων που κινούνται κοντά στο έδαφος είναι επίπεδες (για να μην προδίδουν
τη θέση του ελικοπτέρου από την αντανάκλαση του ήλιου επάνω τους).
Επιπρόσθετα, χρησιμοποιούνται και άλλες συμπληρωματικές
μέθοδοι για να αυξήσουν την αποτελεσματικότητα του stealth συστήματος, όπως απορροφητικές επιφάνειες, ειδικές βαφές κλπ.
Το πρόβλημα όμως είναι ότι αυτό που είναι
καλό για την απόκρυψη είναι κακό για την αεροδυναμική, η οποία γίνεται
αποτελεσματικότερη με τη χρήση καμπύλων επιφανειών.
Την αντίφαση αυτή λύνει η χρήση ισχυρών
και ταχύτατων υπολογιστών, οι οποίοι κάνουν συνεχώς μικροδιορθώσεις στις
επιφάνειες ελέγχου του αεροσκάφους, ώστε να διατηρεί την πορεία που ο πιλότος
του επιλέγει. Στην ουσία ο πιλότος «δείχνει» με τους χειρισμούς του στον
υπολογιστή τι θέλει να εκτελέσει το αεροσκάφος, και ο υπολογιστής φροντίζει να
κινήσει τις επιφάνειες ελέγχου κατάλληλα για να το πετύχει, ενσωματώνοντας όμως
και όλες τις μικροδιορθώσεις που απαιτούνται ώστε το αεροσκάφος να συνεχίζει
πετάει με ευστάθεια και ομαλά. Έτσι
λύνεται το πρόβλημα της αστάθειας, ενώ ισχυρότεροι κινητήρες αντιμετωπίζουν τη
μεγαλύτερη αεροδυναμική αντίσταση του αεροσκάφους, που προκύπτει από τη χρήση πρισματικών
αντί καμπύλων επιφανειών.
85. Η γοητεία των Νεπέριων λογάριθμων.
Για τους
λογάριθμους έγινε σύντομη αναφορά στο θέμα Νο 76, όπου εξηγήθηκε η χρησιμότητά
τους για τους πολλαπλασιασμούς και διαιρέσεις με τη βοήθεια του λογαριθμικού
κανόνα, ο οποίος βρίσκονταν σε χρήση μέχρι τη δεκαετία του ’70.
Οι λογάριθμοι
χρησιμοποιούνται γενικά για να μετρήσουν και να απεικονίσουν μεγέθη που
μεταβάλλονται πολύ έντονα, συνήθως εκθετικά.
Στις
περιπτώσεις αυτές, αν θα έπρεπε να χρησιμοποιηθεί η απλή αναλογική παρουσίαση,
είτε θα χάναμε ευκρίνεια στα μικρά μεγέθη, είτε θα χρειαζόμασταν ένα τεράστιο
χαρτί για να συμπεριληφθούν στην απεικόνιση και τα μεγάλα μεγέθη. Με τη
λογαριθμική απεικόνιση, μπορούμε να έχουμε ακρίβεια και τις δύο άκρες ενός
τέτοιου διαγράμματος σε μία συνολικά πιο «ανθρώπινη» κλίμακα, πχ σε μία σελίδα Α4.
Για
παράδειγμα, μεγέθη όπως η ένταση ενός σεισμού (κλίμακα Ρίχτερ), η ηχητική
ένταση (Ντεσιμπέλ), η οξύτητα ενός διαλύματος (pH), το
μέγεθος (φωτεινότητα) των άστρων κλπ, μετρούνται σε λογαριθμική κλίμακα.
Συγκεκριμένα,
αύξηση κατά μία μονάδα στην κλίμακα Ρίχτερ σημαίνει δεκαπλασιασμό του πλάτους
των σεισμικών δονήσεων, ενώ στα Ντεσιμπέλ (Decibel), επειδή
αναφέρονται σε δέκατα του Μπελ που είναι η μονάδα μέτρησης, η αύξηση κατά δέκα
ντεσιμπέλ αντιστοιχεί σε δεκαπλασιασμό την ηχητικής ισχύος.
Τα
παραπάνω παραδείγματα, αφορούν τους «κοινούς» ή δεκαδικούς λογάριθμους.
Όταν όμως ένα φυσικό φαινόμενο αυξάνεται ραγδαία με σταθερό ποσοστό αύξησης και το αποτέλεσμα της αύξησης προστίθεται κάθε φορά ακέραιο στο αρχικό μέγεθος, κάθε επόμενη αύξηση αφορά το νέο συνολικό ποσό. Το ίδιο ισχύει και σε περίπτωση μείωσης, με τους αντίστοιχους όρους.
Όταν όμως ένα φυσικό φαινόμενο αυξάνεται ραγδαία με σταθερό ποσοστό αύξησης και το αποτέλεσμα της αύξησης προστίθεται κάθε φορά ακέραιο στο αρχικό μέγεθος, κάθε επόμενη αύξηση αφορά το νέο συνολικό ποσό. Το ίδιο ισχύει και σε περίπτωση μείωσης, με τους αντίστοιχους όρους.
Ένα απλό και
κλασικό παράδειγμα είναι ο τοκισμός ενός ποσού, που εφόσον δεν χρησιμοποιούμε
τους τόκους και το επιτόκιο παραμένει σταθερό, το κεφάλαιο αυξάνεται με ρυθμό
που περιγράφεται από ένα συγκεκριμένο είδος λογάριθμου, τον Νεπέριο (από το
λατινοποιημένο όνομα Neper του Σκωτσέζου μαθηματικού του 16ου αι. J. Napier).
Στους
Νεπέριους λογάριθμους, αντί η βάση τους να είναι το 10 όπως στους κοινούς, είναι
κατά προσέγγιση το 2.718 (στην πραγματικότητα τα δεκαδικά του είναι άπειρα,
όπως και του π), και συμβολίζεται με e. Οπότε ο
Νεπέριος λογάριθμος ενός αριθμού Χ είναι η εκθετική δύναμη Τ (που συνήθως
αντιπροσωπεύει χρονικό διάστημα) στην οποία αν υψωθεί το e θα μας
δώσει τον αριθμό X, δηλαδή eT = X.
Ο Νεπέριος
λογάριθμος (συμβολίζεται με ln, ενώ ο κοινός λογάριθμος με log), έχει
βρεθεί ότι περιγράφει πολύ καλά αλλαγές μεγεθών που όπως προαναφέρθηκε το
αποτέλεσμα κάθε φορά «κεφαλαιοποιείται», δηλαδή συμμετέχει αυτούσιο στην
επόμενη φάση της αλλαγής.
Αυτό ισχύει
πέρα από τον ανατοκισμό και σε φυσικά φαινόμενα, όπως στη μεταβολή της τάσης
και έντασης στη φόρτιση / εκφόρτιση ενός πυκνωτή, στη μεταβολή της τάσης και έντασης
μέσα από πηνίο, κλπ.
Συνιστώμενα video στο youtube (αγγλικά): https://www.youtube.com/watch?reload=9&v=1dUSNdZspQc και https://www.youtube.com/watch?v=_-x90wGBD8U
Ο πιο όμορφος τύπος των Μαθηματικών.Συνιστώμενα video στο youtube (αγγλικά): https://www.youtube.com/watch?reload=9&v=1dUSNdZspQc και https://www.youtube.com/watch?v=_-x90wGBD8U
Στον παραπάνω τύπο συγκεντρώνονται τα πιο σημαντικά μαθηματικά μεγέθη: e, i, π, 1, 0 (το i είναι η φανταστική μονάδα, και ισχύει: i2 = −1).
Ξεχωριστή θέση στις εξισώσεις κατέχει και η κυματο-σωματιδιακή εξίσωση του Paul Dirac (εικόνα κάτω), η οποία διατυπώθηκε το 1928 και θεωρείται από κάποιους σαν η "πιο μαγευτική εξίσωση της Φυσικής", καθώς υπονόησε για πρώτη φορά την ύπαρξη αντιύλης.
86. Οι παρεξηγημένοι σπινθήρες.
Ο σπινθήρας έχει επίσης κάποια «κρυφά» χαρακτηριστικά, όπως το ότι σαν φορτίο σ’ ένα ηλεκτρικό κύκλωμα είναι κυρίως «άεργο» (για το άεργο ρεύμα βλέπε το θέμα Νο 22). Ένα άλλο χαρακτηριστικό του είναι ότι συμπεριφέρεται σαν υψίσυχνο ρεύμα εξαιτίας της απότομης ανόδου της τάσης του, με τα προβλήματα και τους περιορισμούς που συνοδεύουν ένα τέτοιο ρεύμα.
Επίσης, ένας σπινθήρας περιέχει υψηλό ποσοστό υπεριώδους ακτινοβολίας που πέρα από τη φωτοπληξία (προσωρινή μείωση όρασης) που μπορεί να προκαλέσει αν είναι αρκετά έντονος, μπορεί να προκαλέσει και μόνιμη βλάβη στα μάτια (όταν πχ οι ηλεκτροσυγκολλητές δεν χρησιμοποιούν την προστατευτική ασπίδα ή τα ειδικά γυαλιά).
Η δημιουργία σπινθήρα στον αέρα, στο επίπεδο της θάλασσας, απαιτεί τάση περίπου 3.000V/mm (η τάση αυτή μειώνεται σημαντικά με το υψόμετρο), αλλά η ένταση εξαρτάται από την πηγή της. Για παράδειγμα, η ισχύς της πηγής είναι επίτηδες περιορισμένη ώστε να μη δημιουργούνται μόνιμες βλάβες στο άνθρωπο από τα συστήματα έναυσης των βενζινοκινητήρων και από τα stun guns (15.000V τα πρώτα, 150.000V τα δεύτερα).
Όπως προαναφέρθηκε, η υψίσυχνη συμπεριφορά του σπινθήρα (επειδή η ροή του ρεύματος δεν είναι ομαλή αλλά γίνεται με έντονες και ταχύτατες αυξομειώσεις και ταλαντώσεις) μεταδίδεται μέσα από τον αέρα (αλλά και το κενό) και δημιουργεί επαγωγικά ρεύματα, δηλαδή προκαλεί τη ροή μικρορευμάτων σε αγώγιμα υλικά ή κυκλώματα, σε κάποια απόσταση.
Αυτό σήμερα είναι ενοχλητικό, επειδή μπορεί να καταστρέψει κοντινά ευαίσθητα ηλεκτρονικά κυκλώματα αν δεν είναι κατάλληλα προστατευμένα, το ίδιο μπορεί να κάνουν και οι κεραυνοί, ενώ οι τελευταίοι παλαιότερα προκαλούσαν παράσιτα στις ραδιοφωνικές λήψεις που δεν ήταν τεχνολογίας FM. Από την άλλη πλευρά, στα πρώτα βήματα της ασύρματης μετάδοσης πληροφορίας, οι σπινθήρες αξιοποιούνταν για τις μεταδόσεις σημάτων Μορς στα πλοία. Τέτοιας τεχνολογίας ήταν πχ ο ασύρματος του Τιτανικού που εξέπεμψε το SOS στο πιο διάσημο ναυάγιο της Ιστορίας.
ΥΓ. Σημαντική είναι η διαφορά του σπινθήρα που ενδεχομένως θα δημιουργηθεί σε ένα κύκλωμα εναλλασσομέμου σε σχέση με ένα συνεχούς ρεύματος, ίδιας τάσης και φορτίου. Κάτι που συμβαίνει φυσιολογικά κάθε φορά που ένας διακόπτης πχ ανοίγει το κύκλωμα, οπότε, ειδικά αν υπάρχουν πυκνωτές ή πηνία συνδεδεμένα ο σπινθήρας είνα ιδιαίτερα έντονος, μακρύς και με διάρκεια. Η εξήγηση είναι ότι στο εναλλασσόμενο ρεύμα των 50Hz, 100 φορές το δευτερόλεπτο η τάση και το ρεύμα μηδενίζονται, κάτι που διευκολύνει σημαντικά στο να σβήσει ο σπινθήρας "εν τη γενέση του".
87. Προσδιορίζοντας την Απροσδιοριστία
Ο Αστυνομικός στον Heisenberg:
Ξέρετε την ταχύτητά σας; – Όχι, αλλά ξέρω τη θέση μου.
Είναι
γνωστό ότι η Κβαντική Φυσική είναι περίεργη και ότι έρχεται ουσιαστικά σε
αντίφαση με την εμπειρία που έχουμε από τον φυσικό κόσμο γύρω μας.
Το ακόμα
πιο περίεργο είναι ότι παρ’ όλη αυτή την ιδιομορφία της, έχει αποδειχτεί
επανειλημμένα ότι «δουλεύει» και μάλιστα πολύ καλά, με αποτέλεσμα ένας μεγάλος
αριθμός εφαρμογών όπως τα μικροηλεκτρονικά, τα laser και οι υπολογιστές να βασίζονται σ’ αυτή.
Ας δούμε
όμως το πιο ιδιόμορφο και δυσνόητο (αλλά και θεμελιώδες) χαρακτηριστικό της
Κβαντικής Φυσικής, που είναι η σχετικά γνωστή διατύπωση ότι είναι αδύνατον να προσδιοριστούν
ταυτόχρονα και με μεγάλη βεβαιότητα η θέση και η ταχύτητα ενός σωματιδίου.
Κατ’
αρχήν έχει αποδειχτεί με το πείραμα της διπλής σχισμής (βλέπε γι’ αυτό κυρίως στο
1ο βίντεο που συστήνεται στο τέλος) ότι τα ηλεκτρόνια συμπεριφέρονται
σαν κύματα* υπό ορισμένες συνθήκες. Μοιάζει μάλιστα να συμπεριφέρονται σαν
κύματα όταν δεν τα παρατηρούμε και σαν σωματίδια όταν τα παρατηρούμε (ή τα
μετράμε)!
*Δεν
είναι όμως σαν τα κλασικά κύματα, αλλά πρόκειται για «κύματα πιθανοτήτων θέσης».
Σύμφωνα με τη σχέση που διατύπωσε ο Γάλλος θεωρητικός Φυσικός Louis de Broglie (ντε
Μπρολί) το 1925, όλα τα κινούμενα σωματίδια ή σώματα συνοδεύονται (ή καλύτερα
εκφράζονται) από ένα κύμα, κάτι σαν τον μανδύα του Σούπερμαν που κυματίζει γύρω
τους καθώς κινούνται. Όμως, με την εξαίρεση των πολύ μικρών σωματιδίων, ο μανδύας αυτός παραμένει ασήμαντα μικρός και κατά συνέπεια αόρατος.
Σύμφωνα
λοιπόν με τον τύπο του ντε Μπρολί , το μήκος κύματος ενός αντικειμένου που
κινείται, είναι αντιστρόφως ανάλογο με την ορμή του, όπως δείχνει η πολύ απλή
σχέση: λ=h/p, όπου:
λ: το μήκος κύματος,
h: μία σταθερά (η σταθερά του Plank) ένας
ΠΑΡΑ ΠΟΛΥ μικρός αριθμός και
p: η ορμή* του σωματιδίου.
*Η ορμή ορίζεται
σαν: μάζα Χ ταχύτητα, οπότε αν
μιλάμε για συγκεκριμένο σωματίδιο, η ορμή εξαρτάται μόνο από την ταχύτητά του.
Τα κύματα
αυτά που δημιουργεί η κίνηση οποιουδήποτε υλικού σώματος ονομάζονται κύματα ντε
Μπρολί ή Υλοκύματα (matter waves).
Από τη
σχέση του ντε Μπρολί είναι φανερό ότι
όσο μικρότερη είναι η ορμή ενός σωματιδίου, δηλαδή όσο μικρότερη η μάζα και η
ταχύτητά του, τόσο μεγαλύτερο θα είναι το μήκος κύματος που το εκφράζει (ή τόσο μικρότερη η συχνότητά του). Στην
πράξη, αυτό σημαίνει ότι μόνο τα πάρα πολύ μικρά (υποατομικά) σωματίδια εκδηλώνουν
την κυματική φύση τους.
Σε σχέση
τώρα με το μήκος κύματος, το οποίο πρέπει να φανταστούμε ότι εκτείνεται σ’ όλη
τη διαδρομή του σωματιδίου, συμβαίνει το εξής: Αν το κύμα με το οποίο «εκφράζεται»
ένα κινούμενο σωματίδιο είναι το τυπικό σταθερά ημιτονικό μιας ορισμένης
συχνότητας, τότε η πιθανότητα το σωματίδιο να βρίσκεται σε κάποια συγκεκριμένη
θέση στη διαδρομή του είναι σχεδόν μηδενική, με άλλα λόγια μπορεί να βρίσκεται σε
οποιοδήποτε σημείο της. Από την άλλη πλευρά, αν το κύμα έχει ένα "συμπύκνωμα" σε
μία περιοχή και είναι πιο "αραιό" σε όλες τις άλλες, είναι σ’ αυτή την περιοχή που προσδιορίζεται
με μεγάλη πιθανότητα η θέση του σωματιδίου. Το πρόβλημα είναι ότι στην
τελευταία περίπτωση για να βρεθεί η ορμή του χρησιμοποιώντας τον τύπο του ντε
Μπρολί, θα πρέπει να είναι γνωστή η συχνότητά του.
Μία
κυματομορφή όμως που δεν είναι σταθερά ημιτονική (μη σταθερά ημιτονική είναι αυτή
στα δεξιά της εικόνας) δεν περιλαμβάνει μία μόνο συχνότητα αλλά ένα πλήθος
(αριστερά στην εικόνα), και μάλιστα όσο αποκλίνει από τη σταθερή ημιτονική
μορφή τόσο μεγαλύτερο είναι το πλήθος των σταθερών ημιτονικών που την
αποτελούν. Αυτές είναι οι γνωστές αρμονικές που ενυπάρχουν σε κάθε μη ημιτονικό
σήμα, οι συχνότητές τους είναι πολλαπλάσια μιας βασικής και προσδιορίζονται με
την ανάλυση Φουριέ.
Για να
επανέλθουμε στην προσπάθεια καθορισμού της συχνότητας του υλοκύματος, είναι
πλέον φανερό ότι όσο πιο έντονο είναι το συμπύκνωμά του, δηλαδή όσο καλύτερα
προσδιορίζεται η θέση του, από τόσες περισσότερες αρμονικές θα αποτελείται το
κύμα του, κάνοντας όλο και λιγότερο πιθανό τον προσδιορισμό μιας συγκεκριμένης συχνότητας,
την οποία όταν θα την εισάγουμε στον τύπο θα μας επιτρέψει να προσδιορίσουμε
την ορμή, και κατ’ επέκταση την ταχύτητά του.
Αυτή
λοιπόν η εγγενής αδυναμία να προσδιοριστεί ταυτόχρονα και με ακρίβεια τόσο η
θέση όσο και η ταχύτητα ενός σωματιδίου, είναι η αρχή της Απροσδιοριστίας ή
αρχή της Αοριστίας που διατύπωσε ο Heisenberg το 1927 και
αποτελεί το θεμέλιο της Κβαντικής Φυσικής, αλλά και έναν από τους μεγαλύτερους
πονοκέφαλους για την κατανόησή της!
Συνιστώμενα
βίντεο:
https://www.youtube.com/watch?v=9QSUsOkptxM (στα ελληνικά).
https://www.youtube.com/watch?reload=9&v=Usu9xZfabPM (στα αγγλικά με ελληνικούς υπότιτλους).
https://www.youtube.com/watch?reload=9&v=Usu9xZfabPM (στα αγγλικά με ελληνικούς υπότιτλους).
88. Ισχύει ο "νόμος του Μέρφυ"; Και το φαινόμενο του "μαύρου κύκνου".
Ο νόμος
του Μέρφυ, που θα μπορούσε επίσης να ονομαστεί και «νόμος της ατυχίας» είναι μία
έκφραση που χρησιμοποιείται συχνά όταν κάτι πάει στραβά και με μη αναμενόμενο
τρόπο.
Αποδίδεται
σε κάποιον Ed Murphy (προφανώς άσχετο με τον ηθοποιό Eddie Murphy), τεχνικό
της Πολεμικής Αεροπορίας των ΗΠΑ στα τέλη της δεκαετίας του ‘40, και η πλήρης
διατύπωσή του σε ελεύθερη μετάφραση είναι: «Αν υπάρχει περίπτωση κάτι να πάει
στραβά, τότε θα πάει στραβά, και μάλιστα τη χειρότερη δυνατή στιγμή και προκαλώντας το μεγαλύτερο πρόβλημα».
Είναι
λογικό βέβαια η φράση αυτή να προέρχεται από τον αεροπορικό κλάδο όπου οι
«ατυχίες» δεν είναι ανεκτές, παρόλα αυτά δεν παύουν να συμβαίνουν.
Φυσικά ο
νόμος έχει προσαρμοστεί σε κάθε επάγγελμα και δραστηριότητα και (καθόλου
περίεργο) αποτελεί αγαπημένη φράση των φοιτητών, κυρίως των λιγότερο καλά
προετοιμασμένων στις εξετάσεις!
Αυτό που
συμβαίνει στην πραγματικότητα είναι ότι ενώ οι βλάβες ενός συστήματος είναι
περίπου τυχαίες (αν και τυπικά είναι συχνότερες
στην αρχή και στο τέλος του κύκλου ζωής του), οι άνθρωποι έχουν την τάση να θυμούνται
κυρίως τις περιπτώσεις που έχουν δημιουργηθεί σημαντικά προβλήματα και ιδιαίτερα
σε δυσμενείς συγκυρίες.
Υπάρχει μια ενδιαφέρουσα
ιστορία για μια αντίστοιχη έκφραση των Γάλλων για μια φέτα ψωμί με
βούτυρο, που όταν πέσει από το τραπέζι συνήθως προσγειώνεται στο έδαφος ανάποδα.
Τελικά, κάποιος μπήκε στον κόπο να ερευνήσει το θέμα θεωρητικά και βρήκε ότι
αυτό δεν είναι και τόσο τυχαίο. Λαμβάνοντας υπ’ όψη τη ροπή αδράνειας μιας
τυπικής φέτας με βούτυρο, το συνηθισμένο ύψος ενός τραπεζιού και υπολογίζοντας την
ταχύτητα περιστροφής όταν το κέντρο βάρος της ξεπεράσει τα όρια του τραπεζιού,
βρήκε ότι πράγματι οι περισσότερες πιθανότητες είναι να προσγειωθεί ανάποδα.
Τελικά
τίποτα δεν είναι τελείως τυχαίο!ΥΓ. Ένα άρθρο του 2023 σχετικά με τα αποτελέσματα από 350757 δοκιμές ρίψης κέρματος (κορώνα - γράμματα) όπου χρησιμοποιήθηκαν πολλοί άνθρωποι και πολλά διαφορετικά κέρματα, έδειξε ότι υπάρχει ελαφρά μεγαλύτερη πιθανότητα (50.8%) να πέσει το κέρμα με την ίδια πλευρά που ήταν προς τα επάνω κατά τη ρίψη του. Αυτό, κατά μία εκτίμηση, αποδίδεται στο ότι η "εκτόξευση" συχνά δεν είναι απόλυτα συμμετρική αλλά παρουσιάζει μια μικρή αστάθεια (ταλάντωση).
Το φαινόμενο ή θεωρία του "μαύρου κύκνου" έγινε ευρύτερα γνωστό εξαιτίας ενός τραγικού συμβάντος που αφορά τη βύθιση του μήκους 56m γιωτ-ιστιοφόρου Bayesian στις 19/8/24, ενώ βρίσκονταν αγκυροβολημένο στα ανοιχτά του Παλέρμο της Σικελίας. Η αιτία ήταν ένας ξαφνικός υδροστρόβιλος που κατά τα φαινόμενα έδωσε μεγάλη κλίση στο σκάφος με το τεράστιο 72m κατάρτι, με αποτέλεσμα να πάρει νερό και να βυθιστεί γρήγορα, παρασέρνοντας στον θάνατο 7 άτομα (άλλα 15 διασώθηκαν).
Το φαινόμενο του "μαύρου κύκνου" αναφέρεται σε έναν πολύ σπάνιο συνδυασμό παραγόντων, που όταν όμως συμβούν έχουν πολύ σοβαρές επιπτώσεις. Συμβάντα που μέχρι εκείνη τη στιγμή θεωρούνταν απίθανα, στη συνέχεια όμως μελετήθηκαν και εξηγήθηκαν. Ο όρος δημιουργήθηκε κατά τη ρωμαϊκή εποχή όταν δεν ήταν γνωστό ότι υπάρχουν μαύροι κύκνοι, μέχρι που ένας εξερευνητής τους εντόπισε στην Αυστραλία, μόλις τον 17ο αι.
89. Ο "παλμός" της Γης.
89. Ο "παλμός" της Γης.
Το 1954,
μετά από δύο χρόνια ερευνών ο Γερμανός καθηγητής Φυσικής W. O. Schumann και ο
συνεργάτης του H. Koning, κατέληξαν στο συμπέρασμα ότι η Γη πρέπει να περιβάλλεται από
στάσιμα ηλεκτρομαγνητικά κύματα πολύ χαμηλής συχνότητας και ισχύος, με μήκος
κύματος συγκρίσιμο με την περίμετρο της Γης, κάτι που επιβεβαιώθηκε από μετρήσεις μερικά χρόνια αργότερα.
Τα κύματα
αυτά που υπάρχουν σχεδόν από τη δημιουργία της Γης (σωστότερα από τη δημιουργία
της ιονόσφαιρας), είναι αποτέλεσμα της κεραυνικής δραστηριότητας στην
ατμόσφαιρα, που εφόσον έχουν τη σωστή συχνότητα (βλ. παρακάτω) ενισχύονται και «παγιδεύονται» σαν στάσιμα ηλεκτρομαγνητικά κύματα μεταξύ
της επιφάνειας της Γης και του κατώτερου τμήματος της ιονόσφαιρας (σε ύψος
περίπου 60 χιλιομέτρων). Κάτι που μοιάζει με αυτό που συμβαίνει μέσα σ' ένα φούρνο μικροκυμάτων, στην περίπτωση του φούρνου βέβαια σε πολύ μεγαλύτερη πυκνότητα ενέργειας και συχνότητα! Η χαμηλότερη συχνότητά τους είναι 7.8 Hz με μήκος
κύματος ίσο με την περίμετρο της Γης, αλλά υπάρχουν και πολλαπλάσιά της. Τα
ηλεκτρομαγνητικά αυτά κύματα ονομάζονται αρκετά εύλογα “συντονισμοί Schumann” (Schumann resonances).
Αυτό που
έχει ενδιαφέρον είναι ότι αυτή η συχνότητα συναντάται τόσο στην ηλεκτρική
δραστηριότητα του ανθρώπινου εγκέφαλου, όσο και σε άλλους βιολογικούς
οργανισμούς, κάνοντας πολλούς να υποθέσουν ότι η έναρξη της ζωής στη Γη
βοηθήθηκε (ή επηρεάστηκε) από αυτή την ηλεκτρομαγνητική δραστηριότητα στην ατμόσφαιρα
σαν αποτέλεσμα των κεραυνών, καθώς μοιάζει να φέρει την «υπογραφή» της.
Μία άλλη αξιοποίηση
των κυμάτων αυτών είναι στη μελέτη της ατμόσφαιρας και του καιρού, καθώς και στη μελέτη της επικοινωνίας με υποβρύχια σε κατάδυση σε οποιοδήποτε
μέρος του κόσμου, καθώς αυτές οι πολύ χαμηλές συχνότητες ταξιδεύουν σ’ όλη τη Γη
και διεισδύουν και σε αρκετό βάθος στη θάλασσα.
91. Μία καμπίνα «φυσαρμόνικα».
90. Η σιωπηλή πτήση της Τυτώς.
Η Τυτώ
είναι ένα είδος κουκουβάγιας (σωστότερα
χαρακτηρίζεται σαν γλαυκόμορφο πτηνό) που στα αγγλικά είναι γνωστή σαν Barn Owl.
‘Έχει
χαρακτηριστικά επίπεδο και κατάλευκο πρόσωπο σε σχήμα καρδιάς. Είναι βασικά νυκτόβιο,
σαρκοφάγο πουλί που κυνηγά συνήθως μικρά τρωκτικά ή και άλλα πουλιά. Η
ιδιαιτερότητα της Τυτώς (όπως και των άλλων κουκουβαγιών) είναι ότι παρά το
σχετικά μεγάλο μέγεθός τους (βάρος λίγο κάτω από μισό κιλό και άνοιγμα φτερών
κάπως μικρότερο από το ένα μέτρο), έχουν μία πρακτικά απόλυτα αθόρυβη πτήση.
Η
ικανότητα αυτή, που φυσικά είναι κρίσιμη για την επιβίωσή της καθώς η τροφή της
μπορεί να κρυφτεί πολύ γρήγορα, επιτυγχάνεται με ειδική κατασκευή των φτερών
της αλλά και ιδιαίτερη τεχνική πτήσης.
Τα εμπρός
μέρος των μεγάλων εξωτερικών πτερών της (με πτερά καλύπτονται τα φτερά ή
πτέρυγες) μοιάζει με τα δόντια ενός χτενιού, αλλά σε μικρογραφία. Αντίστοιχα,
τα πτερά στο πίσω μέρος των φτερών έχουν ένα είδος «ξεφτιών» επίσης
μικροσκοπικών.
Αυτές οι
μικροσκοπικές «χαρακιές» στα πτερά σπάνε τις μεγάλες δίνες που θα δημιουργούσε
η κίνηση του φτερού για την παραγωγή άνωσης και ώσης σε πολλές μικροσκοπικές
δίνες, που το ηχητικό αποτέλεσμα της κάθε μιας είναι ασήμαντο και το άθροισμά
τους απλά δίνει λίγο δυνατότερο ήχο. Για παράδειγμα, χρησιμοποιώντας έναν πίνακα υπολογισμού που υπάρχει στο internet: (http://www.sengpielaudio.com/calculator-spl.htm ), βρίσκουμε ότι αν προσθέσουμε 10 ήχους των 20dB, το
αποτέλεσμα θα είναι ένας ήχος μόνο 30dB.
Επιπλέον,
το εσωτερικότερο τμήμα των φτερών, τόσο από την επάνω πλευρά όσο και από την κάτω,
καλύπτεται από πολύ «αφράτα» πούπουλα που πνίγουν τον ήχο. Με αντίστοιχα
πούπουλα μάλιστα, καλύπτεται και όλο σχεδόν το μήκος των ποδιών της.
Η τεχνική
που χρησιμοποιεί για την πτήση της, βοηθάει επίσης πολύ στο να είναι αθόρυβη,
καθώς η Τυτώ ενεδρεύει σε κάποιο κλαδί και η πτήση μέχρι το θήραμα είναι μια
σύντομη κατολίσθηση με τα φτερά εκτεταμένα και με ελάχιστη κίνησή τους.
Αλλά και
η ακοή και η όραση τη βοηθάει πολύ, καθώς η ακοή, πέρα από εξαιρετική είναι και
«τρισδιάστατη», επειδή ο ένας ακουστικός πόρος βρίσκεται ψηλότερα από τον
άλλον! Η όραση επίσης είναι εξαιρετική, με τίμημα τα μάτια της να είναι κάπως
μακρόστενα και να μην μπορούν να περιστραφούν μέσα στις κόγχες τους. Κάτι που η
Τυτώ (και οι άλλες κουκουβάγιες) αντισταθμίζει με τη δυνατότητα περιστροφής του
κεφαλιού της κατά ¾ του κύκλου (270
μοίρες), από κάθε πλευρά.
Είναι
χαρακτηριστικό, ότι η κουκουβάγια του χιονιού (Snowy Owl) ακούει
τρωκτικά που κινούνται ακόμα και κάτω από παχύ χιόνι, και πετώντας με ακρίβεια
στο σημείο εκείνο βυθίζει τα νύχια της «στα τυφλά» και τα αρπάζει.
Δείτε στο
παρακάτω βίντεο, ηχητική σύγκριση της πτήσης της Τυτώς με άλλα πουλιά: https://www.youtube.com/watch?v=-WigEGNnuTE
Η τεχνική
της δημιουργίας πολλών μικρών στροβίλων για την αποφυγή ενός μεγαλύτερου που
περιγράφηκε παραπάνω, είναι γνωστή και εφαρμόζεται στην αεροναυτική, όχι κατ’
αρχήν για τη μείωση του θορύβου, αλλά για τη διατήρηση της ροής του αέρα ομαλής
στο επάνω μέρος της πτέρυγας, ακόμα και σε μεγάλη γωνία προσβολής (γωνία με την
οποία ο φαινόμενος άνεμος συναντά την πτέρυγα).
Αυτό
γίνεται με την τοποθέτηση πολλών μικρών προεξοχών (vortex generators) κατά
μήκος της πτέρυγας, σε συγκεκριμένα σημεία. Ίσως κάποτε, όταν ο θόρυβος των αεροπορικών
κινητήρων μειωθεί σημαντικά (έχει ήδη γίνει αρκετή πρόοδος προς αυτή την
κατεύθυνση), τα φτερά της Τυτώς να εμπνεύσουν και μεθόδους μείωσης του θορύβου που
προέρχονται από την κίνηση των αεροσκαφών μέσα στον αέρα.
91. Μία καμπίνα «φυσαρμόνικα».
Μερικοί απλοί υπολογισμοί δείχνουν ότι η επιμήκυνση μιας καμπίνας μήκους 40m, διαμέτρου 4m και πάχους τοιχώματος 3mm, εξαιτίας της διαφοράς πίεσης είναι της τάξης των μερικών χιλιοστών. Για τον υπολογισμό αυτόν έχει ληφθεί υπόψη και η συρρίκνωση του μήκους της καμπίνας εξαιτίας του φαινομένου του Poisson, σύμφωνα με το οποίο η αύξηση της πίεσης σ’ έναν κλειστό σωλήνα καθώς προκαλεί αύξηση (έστω ελάχιστη) της διαμέτρου του μειώνει αντίστοιχα το μήκος του, με αποτέλεσμα η τελική επιμήκυνση να είναι μικρή. Μάλιστα από τους υπολογισμούς προκύπτει ότι το μεγαλύτερο μέρος της εν δυνάμει επιμήκυνσης από την πίεση, αναιρείται από τη βράχυνση εξαιτίας του φαινομένου Poisson.
Υπάρχει όμως ένας παράγοντας πολύ πιο σημαντικός από τους προηγούμενους. Καθώς στο τυπικό ύψος πτήσης επικρατεί θερμοκρασία γύρω στους -50C, και εφόσον θεωρήσουμε ότι στο έδαφος η θερμοκρασία είναι +20C, η άτρακτος υποβάλλεται σε μια συνολική διαφορά θερμοκρασίας 70C, που δίνει βράχυνση της ατράκτου (στο προηγούμενο παράδειγμα) στο ύψος πτήσης, γύρω στα 70mm.*
Αυτός προφανώς είναι ένας πολύ πιο σημαντικός παράγοντας από την επιμήκυνση, άρα τελικά στο ύψος πτήσης η καμπίνα σαφώς μειώνεται παρά αυξάνεται σε μήκος.
Υπάρχει (ή μάλλον υπήρχε) μια εντυπωσιακή εξαίρεση. Το Concorde σε υπερηχητική πτήση επιμηκύνονταν σχεδόν κατά 20 εκατοστά, καθώς στην περίπτωση αυτή επικρατούσε η διαστολή από τη θέρμανσή του (περίπου στους 100C) εξαιτίας της τριβής με την ατμόσφαιρα**, που βέβαια προστίθετο στην (πολύ μικρότερη όμως) επιμήκυνση εξαιτίας της διαφοράς πίεσης. Εξαίρεση αποτελούσε επίσης το λιγότερο γνωστό αμερικανικό κατασκοπευτικό αεροσκάφος SR-71, που με ταχύτητα μεγαλύτερη από τριπλάσια του ήχου θερμαίνονταν τόσο, που έπρεπε να κατασκευαστεί από τιτάνιο για να αντέξει. Η επιμήκυνσή του ήταν περίπου η μισή του Concorde, καθώς είχε το μισό του μήκος και το τιτάνιο έχει λιγότερο από τον μισό συντελεστή διαστολής του αλουμινίου (επιπλέον είχε μόνον τον θάλαμο διακυβέρνησης συμπιεσμένο).
*Στην πραγματικότητα λιγότερη, καθώς το αεροσκάφος θερμαίνεται ελαφρά από την τριβή και τη συμπίεση του αέρα (βλ και παρατήρηση **) αλλά και εξαιτίας θερμικών διαρροών από τον αέρα της καμπίνας παρά τη θερμομόνωση.
**Αν και έχει επικρατήσει αυτή η εξήγηση για τη θέρμανση σε πολύ μεγάλες ταχύτητες, πρόκειται ουσιαστικά για αδιαβατική θέρμανση του αέρα εξαιτίας της έντονης επιβράδυνσης και συμπίεσής του στις εμπρόσθιες επιφάνειες, ένα φαινόμενο παρόμοιο με αυτό που συμβαίνει κατά τη συμπίεση των κινητήρων ντίζελ!
(Για διάκριση μεταξύ Άνωσης και Άντωσης, βλ θέμα Νο 13).
Τι είναι όμως αυτό που την προκαλεί στην πραγματικότητα;
Όσο και να φαίνεται παράξενο, είναι η διαφορά στην εξωτερική πίεση που υπάρχει μεταξύ της κάτω και της επάνω επιφάνειας του αντικειμένου, εξαιτίας της υψομετρικής τους διαφοράς (ενώ στις πλευρικές επιφάνειες, οι δυνάμεις που οφείλονται στην πίεση αλληλοεξουδετερώνονται).
Ας φανταστούμε έναν κύβο πλευράς ενός μέτρου. Η επάνω και η κάτω επιφάνειά του είναι προφανώς 1m2, και απέχουν μεταξύ τους 1m. Η ατμοσφαιρική πίεση στο ύψος της θάλασσας και για 15 οC (βλέπε: https://www.mide.com/air-pressure-at-altitude-calculator) είναι 101325.00Pa, ενώ ένα μόλις μέτρο ψηλότερα είναι 101319.99Pa. Η διαφορά των πιέσεων (12.01Pa) πολλαπλασιασμένη με την επιφάνεια του 1m2 μας δίνει τη δύναμη προς τα επάνω (άνωση), δηλαδή 12Ν.
Η δύναμη αυτή αντιστοιχεί στο βάρος ακριβώς 1m3 αέρα στις ίδιες συνθήκες, δηλαδή στην ποσότητα του αέρα που λείπει, το οποίο βάρος σύμφωνα με τη θεωρία της άνωσης ισούται (σε μέγεθος) με τη δύναμη της άνωσης που ασκεί ο αέρας στον όγκο αυτόν.
Επειδή πρακτικά δεν μπορούμε να έχουμε απόλυτο κενό σε όγκο 1m3 χωρίς μία πολύ ισχυρή (και βαριά) κατασκευή, μπορούμε να υπολογίσουμε τον ίδιο όγκο γεμάτο με αέριο ήλιο σε αντίστοιχη πίεση και θερμοκρασία, οπότε το βάρος του είναι περίπου 1.7Ν.
Άρα, αν θέλουμε να κατασκευάσουμε ένα αερόστατο 1m3 με ήλιο, θα έχουμε καθαρή άνωση στην επιφάνεια της θάλασσας περίπου 10Ν/m3, χωρίς να υπολογίσουμε το βάρος του περιβλήματος κλπ.
Δηλαδή, η άνωση ουσιαστικά οφείλεται στην διαφορά πίεσης του περιβάλλοντος μέσου (αέρα ή νερού) στο οριζόντιο τμήμα των επιφανειών ενός σώματος, που έχουν κάποια απόσταση κατακόρυφα. Βέβαια ο αέρας και το νερό έχουν δύο σημαντικές διαφορές, τη μεγάλη διαφορά πυκνότητας και ότι ο αέρας, σε αντίθεση με το νερό, είναι συμπιεστός, γι’ αυτό και η αλλαγή της πυκνότητας και της πίεσής του με το υψόμετρο είναι εκθετική.
Μία συνέπεια της σημαντικής αλλαγής της πίεσης του αέρα με το υψόμετρο, είναι ότι τα αεροσκάφη παρουσιάζουν φυσική ευστάθεια ως προς το ύψος πτήσης, καθώς έχουν την τάση να παραμένουν στην ίδια πυκνότητα ατμόσφαιρας, για δεδομένη ταχύτητα και σε οριζόντια πτήση. Αυτό δεν ισχύει για τα υποβρύχια σε κατάδυση, καθώς το νερό εξαιτίας της γραμμικής αύξησης της πίεσης με το βάθος, παρουσιάζει πάντα σταθερή διαφορά πίεσης* μεταξύ της κάτω και της επάνω επιφάνειας του σκάφους. Κάτι όμως που αντίστοιχα δεν ισχύει για τα αερόστατα, όπου εξαιτίας της εκθετικής αλλαγής της πίεσης του αέρα, η διαφορά αυτή είναι μοναδική σε κάθε σημείο του ύψους αιώρησης.
Τι είναι όμως αυτό που την προκαλεί στην πραγματικότητα;
Όσο και να φαίνεται παράξενο, είναι η διαφορά στην εξωτερική πίεση που υπάρχει μεταξύ της κάτω και της επάνω επιφάνειας του αντικειμένου, εξαιτίας της υψομετρικής τους διαφοράς (ενώ στις πλευρικές επιφάνειες, οι δυνάμεις που οφείλονται στην πίεση αλληλοεξουδετερώνονται).
Ας φανταστούμε έναν κύβο πλευράς ενός μέτρου. Η επάνω και η κάτω επιφάνειά του είναι προφανώς 1m2, και απέχουν μεταξύ τους 1m. Η ατμοσφαιρική πίεση στο ύψος της θάλασσας και για 15 οC (βλέπε: https://www.mide.com/air-pressure-at-altitude-calculator) είναι 101325.00Pa, ενώ ένα μόλις μέτρο ψηλότερα είναι 101319.99Pa. Η διαφορά των πιέσεων (12.01Pa) πολλαπλασιασμένη με την επιφάνεια του 1m2 μας δίνει τη δύναμη προς τα επάνω (άνωση), δηλαδή 12Ν.
Η δύναμη αυτή αντιστοιχεί στο βάρος ακριβώς 1m3 αέρα στις ίδιες συνθήκες, δηλαδή στην ποσότητα του αέρα που λείπει, το οποίο βάρος σύμφωνα με τη θεωρία της άνωσης ισούται (σε μέγεθος) με τη δύναμη της άνωσης που ασκεί ο αέρας στον όγκο αυτόν.
Επειδή πρακτικά δεν μπορούμε να έχουμε απόλυτο κενό σε όγκο 1m3 χωρίς μία πολύ ισχυρή (και βαριά) κατασκευή, μπορούμε να υπολογίσουμε τον ίδιο όγκο γεμάτο με αέριο ήλιο σε αντίστοιχη πίεση και θερμοκρασία, οπότε το βάρος του είναι περίπου 1.7Ν.
Άρα, αν θέλουμε να κατασκευάσουμε ένα αερόστατο 1m3 με ήλιο, θα έχουμε καθαρή άνωση στην επιφάνεια της θάλασσας περίπου 10Ν/m3, χωρίς να υπολογίσουμε το βάρος του περιβλήματος κλπ.
Δηλαδή, η άνωση ουσιαστικά οφείλεται στην διαφορά πίεσης του περιβάλλοντος μέσου (αέρα ή νερού) στο οριζόντιο τμήμα των επιφανειών ενός σώματος, που έχουν κάποια απόσταση κατακόρυφα. Βέβαια ο αέρας και το νερό έχουν δύο σημαντικές διαφορές, τη μεγάλη διαφορά πυκνότητας και ότι ο αέρας, σε αντίθεση με το νερό, είναι συμπιεστός, γι’ αυτό και η αλλαγή της πυκνότητας και της πίεσής του με το υψόμετρο είναι εκθετική.
Μία συνέπεια της σημαντικής αλλαγής της πίεσης του αέρα με το υψόμετρο, είναι ότι τα αεροσκάφη παρουσιάζουν φυσική ευστάθεια ως προς το ύψος πτήσης, καθώς έχουν την τάση να παραμένουν στην ίδια πυκνότητα ατμόσφαιρας, για δεδομένη ταχύτητα και σε οριζόντια πτήση. Αυτό δεν ισχύει για τα υποβρύχια σε κατάδυση, καθώς το νερό εξαιτίας της γραμμικής αύξησης της πίεσης με το βάθος, παρουσιάζει πάντα σταθερή διαφορά πίεσης* μεταξύ της κάτω και της επάνω επιφάνειας του σκάφους. Κάτι όμως που αντίστοιχα δεν ισχύει για τα αερόστατα, όπου εξαιτίας της εκθετικής αλλαγής της πίεσης του αέρα, η διαφορά αυτή είναι μοναδική σε κάθε σημείο του ύψους αιώρησης.
*Εκτός αν υπάρχουν στρώματα νερού διαφορετικής θερμοκρασίας, οπότε διαφοροποιείται αντίστοιχα η πυκνότητα και η πίεσή τους τους.
Έτσι λοιπόν, αυτό που παρουσιάζεται σε μερικές ταινίες για εντυπωσιασμό, δηλαδή το γρήγορο πάγωμα ενός αστροναύτη αν εκτεθεί στο κενό του Διαστήματος, δεν είναι αληθινό, καθώς ο αστροναύτης θα παγώσει βέβαια αλλά με πολύ πιο αργό ρυθμό, καθώς το κενό είναι το καλύτερο μονωτικό.
Η εντύπωση αυτή έχει μάλλον προκύψει από το άμεσο πάγωμα του νερού που αποβάλλεται από ένα διαστημόπλοιο, κάτι που έχει καταγραφεί σε πραγματικές συνθήκες. Στην περίπτωση αυτή όμως, το πάγωμα προκαλείται από την άμεση εξάτμιση μέρους του νερού καθώς βρίσκεται σε απόλυτο κενό αέρα, μέχρι το ταχύτατο πάγωμα της υπόλοιπης μάζας του νερού να επιβραδύνει την εξάτμισή του.
Ακόμα, σε μερικές ταινίες, επίσης για λόγους εντυπωσιασμού, παρουσιάζεται ότι η ολική απώλεια πίεσης μιας διαστημικής στολής οδηγεί στον άμεσο θάνατο του αστροναύτη και μάλιστα με εντυπωσιακό τρόπο (σκάσιμο!). Στην πραγματικότητα, σε μια τέτοια περίπτωση ο αστροναύτης διατηρεί τις αισθήσεις του για αρκετά δευτερόλεπτα και μπορεί να επανέλθει αν του παρασχεθεί οξυγόνο μέχρι και μετά από δύο λεπτά. Αυτό έχει συμβεί στο έδαφος εξαιτίας ατυχήματος, σε δοκιμές σε συνθήκες τεχνητού κενού, και ο αστροναύτης επέζησε χωρίς μακροχρόνιες επιπτώσεις στην υγεία του.
94. Μια απίθανη αντανάκλαση.
Είναι γνωστό ότι η απόσταση Γης – Σελήνης έχει μετρηθεί με μεγάλη ακρίβεια από τη στιγμή που οι αστροναύτες του Απόλλων 11 άφησαν στην επιφάνεια της Σελήνης έναν ανακλαστήρα, όπως έγινε και σε μεταγενέστερες αποστολές.
Πώς όμως μια δέσμη laser από τη Γη σημάδεψε με ακρίβεια έναν ανακλαστήρα διαστάσεων περίπου 0.5m Χ 0.5m σε απόσταση 400.000km και έλαβε πίσω το σήμα με τόση ακρίβεια;
Στο μυαλό μας έχουμε τη δέσμη laser σαν μία πολύ στενή δέσμη που δεν «ανοίγει» επειδή αποτελείται αυστηρά από μονοχρωματική ακτινοβολία. Και αυτό είναι σωστό για τα μέτρα και τις αποστάσεις επάνω στη Γη, καθώς στην πραγματικότητα η δέσμη ανοίγει σταδιακά, αλλά τόσο λίγο που για τις μετρήσεις στη Γη δεν έχει σημασία.
Η δέσμη όμως αυή (στην ουσία παλμοσειρά) που ξεκινάει με διάμετρο 3.5m από τη Γη, φτάνει στη Σελήνη με διάμετρο 2km (!) και παρόλα αυτά για να «πετύχει» τον ανακλαστήρα απαιτείται σκόπευση πολύ μεγάλης ακρίβειας. Ας υποθέσουμε λοιπόν ότι η δέσμη βρήκε τελικά τον ανακλαστήρα, πώς όπως το σήμα επέστρεψε με τέτοια ακρίβεια ώστε να φτάσει πίσω στη Γη, μετά από περίπου 2.5s;
Μοιάζει απίθανο, επειδή συνήθως έχουμε στο μυαλό μας τον ανακλαστήρα σαν μια επίπεδη επιφάνεια, οπότε αν η δέσμη που προσπίπτει δεν είναι τελείως κάθετη στην επιφάνειά του, δεν επιστρέφει από την ίδια διαδρομή. Όμως, αν ο ανακλαστήρας αποτελείται από τρείς αντανακλαστικές επιφάνειες κάθετες μεταξύ τους ώστε να σχηματίζουν το εσωτερικό μιας γωνίας κύβου πχ (βλ εικόνα),
Είναι γνωστό ότι η απόσταση Γης – Σελήνης έχει μετρηθεί με μεγάλη ακρίβεια από τη στιγμή που οι αστροναύτες του Απόλλων 11 άφησαν στην επιφάνεια της Σελήνης έναν ανακλαστήρα, όπως έγινε και σε μεταγενέστερες αποστολές.
Πώς όμως μια δέσμη laser από τη Γη σημάδεψε με ακρίβεια έναν ανακλαστήρα διαστάσεων περίπου 0.5m Χ 0.5m σε απόσταση 400.000km και έλαβε πίσω το σήμα με τόση ακρίβεια;
Στο μυαλό μας έχουμε τη δέσμη laser σαν μία πολύ στενή δέσμη που δεν «ανοίγει» επειδή αποτελείται αυστηρά από μονοχρωματική ακτινοβολία. Και αυτό είναι σωστό για τα μέτρα και τις αποστάσεις επάνω στη Γη, καθώς στην πραγματικότητα η δέσμη ανοίγει σταδιακά, αλλά τόσο λίγο που για τις μετρήσεις στη Γη δεν έχει σημασία.
Η δέσμη όμως αυή (στην ουσία παλμοσειρά) που ξεκινάει με διάμετρο 3.5m από τη Γη, φτάνει στη Σελήνη με διάμετρο 2km (!) και παρόλα αυτά για να «πετύχει» τον ανακλαστήρα απαιτείται σκόπευση πολύ μεγάλης ακρίβειας. Ας υποθέσουμε λοιπόν ότι η δέσμη βρήκε τελικά τον ανακλαστήρα, πώς όπως το σήμα επέστρεψε με τέτοια ακρίβεια ώστε να φτάσει πίσω στη Γη, μετά από περίπου 2.5s;
Μοιάζει απίθανο, επειδή συνήθως έχουμε στο μυαλό μας τον ανακλαστήρα σαν μια επίπεδη επιφάνεια, οπότε αν η δέσμη που προσπίπτει δεν είναι τελείως κάθετη στην επιφάνειά του, δεν επιστρέφει από την ίδια διαδρομή. Όμως, αν ο ανακλαστήρας αποτελείται από τρείς αντανακλαστικές επιφάνειες κάθετες μεταξύ τους ώστε να σχηματίζουν το εσωτερικό μιας γωνίας κύβου πχ (βλ εικόνα),
τότε μετά από τρείς διαδοχικές αντανακλάσεις στις επιφάνειες η δέσμη επιστρέφει πίσω ακριβώς από την ίδια διαδρομή, ανεξάρτητα από τη γωνία της αρχικής πρόσπτωσης! Στην ίδια αρχή στηρίζονται και οι ανακλαστήρες δεσμών φωτός, υπέρυθρων ή laser σε τεχνικές εφαρμογές. Φυσικά, περιέχουν πολλές μικρές τέτοιες γωνίες και όχι μία μεγάλη.
Καθώς ο ανακλαστήρας από τη Σελήνη στέλνει πίσω ένα ελάχιστο ποσοστό της αρχικής δέσμης, το οποίο επίσης «απλώνεται» σε διάμετρο 15km έχοντας φτάσει στη Γη, το τελικό ποσοστό ακτινοβολίας που επιστρέφει στον ανιχνευτή είναι ελάχιστο, μόλις ένα φωτόνιο στα 10 με εκθέτη 15(!), κάτι που επιβάλει τη χρήση πολύ ευαίσθητων συσκευών, παρόλο που τόσο η εκπομπή όσο και η λήψη γίνονται σε υψόμετρο για να μειωθεί η απορρόφηση από την ατμόσφαιρα. Επιπλέον, καθώς η Γη περιστρέφεται, το χρονικό «άνοιγμα» για την ανίχνευση είναι πολύ μικρό. Από την άλλη πλευρά, το «άπλωμα» της δέσμης που επιστρέφει, επιτρέπει την ανίχνευσή της από πολλά διαφορετικά σημεία στη Γη.
95. «Κώνος του Mach» για το φως;
Λίγο πολύ η δημιουργία υπερηχητικού κώνου είναι γνωστή. Σφαίρες, βλήματα πυροβολικού, πύραυλοι και μαχητικά αεροπλάνα μπορούν να τον δημιουργήσουν, αρκεί να κινηθούν ταχύτερα από την ταχύτητα διάδοσης του ήχου στις συγκεκριμένες συνθήκες.
Ο κώνος αυτός δεν φαίνεται με το μάτι (αν και η συμπύκνωση των υδρατμών γύρω από το αεροπλάνο ακριβώς πριν τη διάσπαση του φράγματος του ήχου μαρτυρεί την αρχή της δημιουργίας του), φαίνεται όμως πολύ καλά χρησιμοποιώντας τη φωτογραφική τεχνική Schlieren.
Εκεί όμως που όλοι έχουμε δει έναν «υπερηχητικό κώνο» (αν και στη δισδιάστατη εκδοχή του) είναι στη θάλασσα, όπου η ταχύτητα μετάδοσης των κυμάτων είναι πολύ μικρή, οπότε όταν ένα σκάφος κινείται (εκτός αν κινείται πολύ αργά) αφήνει πίσω του έναν κυματισμό σχήματος Λ, και αν προσέξουμε, στο όρια του Λ το κύμα είναι εντονότερο.
Συνεπώς, σε κάθε μέσο που έχει κυματική φύση, μια κίνηση υλικού σώματος γρηγορότερα από την ταχύτητα μετάδοσης του κύματος, προκαλεί τον χαρακτηριστικό κώνο ή κώνο του Mach όπως έχει επικρατήσει να λέγεται για τον αέρα, όπου το φαινόμενο είναι πιο χαρακτηριστικό, καθώς συνοδεύεται και από έντονο κρότο.
Θα μπορούσε όμως να συμβεί το ίδιο και με το φως, μια και το φως έχει επίσης κυματική φύση;
Η απάντηση είναι θετική, και αυτό ακριβώς το φαινόμενο είναι γνωστό σαν ακτινοβολία Cherenkov, που είναι η γαλάζια λάμψη που βλέπουμε σε μικρούς πυρηνικούς αντιδραστήρες μέσα σε δεξαμενές νερού.
Στην εύλογη ερώτηση, πώς είναι αυτό δυνατόν μια και τίποτα δεν κινείται ταχύτερα από το φως, η απάντηση είναι ότι πράγματι δεν υπάρχει ταχύτητα μεγαλύτερη από αυτή του φωτός, αλλά στο κενό.
Μέσα σε οπτικά μέσα, όπως στο γυαλί, στα διαφανή πλαστικά, στο νερό κλπ, το φως έχει μικρότερη ταχύτητα (ταχύτητα διάδοσης), οπότε ένα σωματίδιο θα μπορούσε να κινηθεί ταχύτερα από το φως σ’ αυτό το περιβάλλον.
Η κίνηση μάλιστα ενός σωματιδίου ταχύτερα από το φως ειδικά στο νερό, δημιουργεί έναν κώνο φωτονίων (φωτονικό κώνο) στο μήκος κύματος του γαλάζιου του οπτικού φάσματος, που κάνει το νερό (στην περίπτωση της δεξαμενής) να λάμπει μ’ ένα απόκοσμο γαλάζιο φως.
Το πολύ ενδιαφέρον είναι ότι το 2017 Αμερικανοί επιστήμονες κατάφεραν να φωτογραφίσουν έναν εξαιρετικά σύντομο παλμό πράσινου laser με τον φωτεινό κώνο πίσω του, ακριβώς όπως θα βλέπαμε στο ηχητικό του ανάλογο. Για τη φωτογράφιση αυτή χρειάστηκε μια εξαιρετικής ταχύτητας φωτογραφική διάταξη, ικανή για ένα τρισεκατομμύριο λήψεις το δευτερόλεπτο!
Μέσα σε οπτικά μέσα, όπως στο γυαλί, στα διαφανή πλαστικά, στο νερό κλπ, το φως έχει μικρότερη ταχύτητα (ταχύτητα διάδοσης), οπότε ένα σωματίδιο θα μπορούσε να κινηθεί ταχύτερα από το φως σ’ αυτό το περιβάλλον.
Η κίνηση μάλιστα ενός σωματιδίου ταχύτερα από το φως ειδικά στο νερό, δημιουργεί έναν κώνο φωτονίων (φωτονικό κώνο) στο μήκος κύματος του γαλάζιου του οπτικού φάσματος, που κάνει το νερό (στην περίπτωση της δεξαμενής) να λάμπει μ’ ένα απόκοσμο γαλάζιο φως.
Το πολύ ενδιαφέρον είναι ότι το 2017 Αμερικανοί επιστήμονες κατάφεραν να φωτογραφίσουν έναν εξαιρετικά σύντομο παλμό πράσινου laser με τον φωτεινό κώνο πίσω του, ακριβώς όπως θα βλέπαμε στο ηχητικό του ανάλογο. Για τη φωτογράφιση αυτή χρειάστηκε μια εξαιρετικής ταχύτητας φωτογραφική διάταξη, ικανή για ένα τρισεκατομμύριο λήψεις το δευτερόλεπτο!
Το φως στον κώνο, είναι το αντίστοιχο του κρότου που δημιουργεί ο κώνος του Mach στον αέρα, που τον ακούμε όταν φτάσει στο σημείο που βρισκόμαστε, συνήθως στο έδαφος.
96. Μια «φτηνή» βόλτα στο Διάστημα (σχετικό είναι επίσης και το θέμα Νο 67).
Δεν πρόκειται για σχήμα λόγου, αλλά για μια πραγματικά τεράστια διαφορά που υπάρχει μεταξύ του να τεθεί ένας θάλαμος* σε τροχιά γύρω από τη Γη, με αυτή του να βρεθεί «απλώς» στο Διάστημα, δηλαδή σε υψόμετρο πάνω από τα 100km που θεωρητικά ξεκινάει το Διάστημα (γραμμή Κάρμαν).
Η διαφορά είναι πολύ μεγάλη ενεργειακά, γιατί ενώ στην πρώτη περίπτωση θα πρέπει να αναπτύξει μία ταχύτητα περίπου 29.000km/h, στη δεύτερη αρκεί να απλά να φθάσει στο ύψος των 100km, ώστε ο (ενδεχόμενος) επιβάτης του να πάρει το «χρίσμα» του αστροναύτη.
Και στις δύο περιπτώσεις θα πρέπει να δαπανηθεί ενέργεια (σε μορφή καυσίμου φυσικά) για την άνοδο στο ύψος αυτό, αλλά στην πρώτη περίπτωση θα πρέπει να δαπανηθεί πολύ περισσότερη επιπλέον ενέργεια για να επιταχύνει το διαστημόπλοιο στην απαιτούμενη ταχύτητα τροχιάς.
Αν θέλουμε να συγκρίνουμε ενεργειακά τις δύο περιπτώσεις, δηλαδή τη χαμηλή τροχιά στα 100km με την απλή άνοδο στα 100km (υποτροχιακή ή βαλλιστική πτήση), προκύπτει ότι στην πρώτη περίπτωση απαιτείται 32 φορές περισσότερη ενέργεια από τη δεύτερη (!), για το ίδιο βάρος θαλάμου φυσικά.
Μάλιστα, για σύγκριση, αν θέλουμε να ξεφύγουμε τελείως από το βαρυτικό πεδίο της Γης, χρειάζεται διπλάσια ενέργεια από αυτή της χαμηλής τροχιάς.
Βέβαια, η χαμηλή τροχιά των 100km δεν θα μπορεί να κρατηθεί για πολύ χωρίς διορθώσεις (επιπλέον δαπάνη ενέργειας), καθώς η τριβή με τα υπολείμματα της ατμόσφαιρας ακόμα και σ’ αυτό το ύψος δεν είναι αμελητέα. Για σύγκριση, ο Διεθνής Διαστημικός Σταθμός που η τροχιά του βρίσκεται γύρω στα 400km** χρειάζεται διόρθωση κάθε δεύτερη εβδομάδα εξαιτίας των μορίων της ατμόσφαιρας που υπάρχουν ακόμα και σ’ αυτό το ύψος.
96. Μια «φτηνή» βόλτα στο Διάστημα (σχετικό είναι επίσης και το θέμα Νο 67).
Δεν πρόκειται για σχήμα λόγου, αλλά για μια πραγματικά τεράστια διαφορά που υπάρχει μεταξύ του να τεθεί ένας θάλαμος* σε τροχιά γύρω από τη Γη, με αυτή του να βρεθεί «απλώς» στο Διάστημα, δηλαδή σε υψόμετρο πάνω από τα 100km που θεωρητικά ξεκινάει το Διάστημα (γραμμή Κάρμαν).
Η διαφορά είναι πολύ μεγάλη ενεργειακά, γιατί ενώ στην πρώτη περίπτωση θα πρέπει να αναπτύξει μία ταχύτητα περίπου 29.000km/h, στη δεύτερη αρκεί να απλά να φθάσει στο ύψος των 100km, ώστε ο (ενδεχόμενος) επιβάτης του να πάρει το «χρίσμα» του αστροναύτη.
Και στις δύο περιπτώσεις θα πρέπει να δαπανηθεί ενέργεια (σε μορφή καυσίμου φυσικά) για την άνοδο στο ύψος αυτό, αλλά στην πρώτη περίπτωση θα πρέπει να δαπανηθεί πολύ περισσότερη επιπλέον ενέργεια για να επιταχύνει το διαστημόπλοιο στην απαιτούμενη ταχύτητα τροχιάς.
Αν θέλουμε να συγκρίνουμε ενεργειακά τις δύο περιπτώσεις, δηλαδή τη χαμηλή τροχιά στα 100km με την απλή άνοδο στα 100km (υποτροχιακή ή βαλλιστική πτήση), προκύπτει ότι στην πρώτη περίπτωση απαιτείται 32 φορές περισσότερη ενέργεια από τη δεύτερη (!), για το ίδιο βάρος θαλάμου φυσικά.
Μάλιστα, για σύγκριση, αν θέλουμε να ξεφύγουμε τελείως από το βαρυτικό πεδίο της Γης, χρειάζεται διπλάσια ενέργεια από αυτή της χαμηλής τροχιάς.
Βέβαια, η χαμηλή τροχιά των 100km δεν θα μπορεί να κρατηθεί για πολύ χωρίς διορθώσεις (επιπλέον δαπάνη ενέργειας), καθώς η τριβή με τα υπολείμματα της ατμόσφαιρας ακόμα και σ’ αυτό το ύψος δεν είναι αμελητέα. Για σύγκριση, ο Διεθνής Διαστημικός Σταθμός που η τροχιά του βρίσκεται γύρω στα 400km** χρειάζεται διόρθωση κάθε δεύτερη εβδομάδα εξαιτίας των μορίων της ατμόσφαιρας που υπάρχουν ακόμα και σ’ αυτό το ύψος.
Υπάρχει και κάτι άλλο. Η επιστροφή. Τα διαστημόπλοια σε τροχιά πρέπει να ξοδέψουν την τεράστια κινητική τους ενέργεια σε θερμότητα για να «φρενάρουν» αρκετά ώστε να επιτρέψουν στη βαρύτητα να κάνει τη δουλειά της μέσα σε εύλογο χρονικό διάστημα. Συνεπώς χρειάζονται μια πολύ ειδική, βαριά και ακριβή αντιθερμική προστασία, και επιπλέον πολύ ακριβείς υπολογισμούς για τη γωνία επανεισόδου στην ατμόσφαιρα, κάτι που δεν το χρειάζονται καθόλου οι θάλαμοι βαλλιστικής τροχιάς.
Μια ενδιάμεση λύση, όχι όμως για μεγάλα φορτία είναι η εναέρια εκτόξευση, όπου ένα μεγάλο τροποποιημένο αεροσκάφος (πχ Boeing 747) ανεβάζει όσο το δυνατόν ψηλότερα το φορτίο (συνήθως έναν μικρό δορυφόρο) που θα τεθεί σε τροχιά προσαρμοσμένο σ' έναν πύραυλο, και στη συνέχεια το αποδεσμεύει για να μπει σε τροχιά (σε πολύ μεγαλύτερο υψόμετρο και με μεγαλύτερη ταχύτητα) με τη βοήθεια του πυραύλου του. Αυτή η μέθοδος έχει το πλεονέκτημα της σημαντικής εξοικονόμησης καυσίμου κατά την αρχική φάση της πτήσης, καθώς χρησιμοποιείται η αεροδυναμική άντωση του αεροσκάφους-φορέα και οι jet κινητήρες του, αλλά και της πιο αποδοτικής προσαρμογής του ακροφυσίου του πυραύλου, καθώς θα λειτουργήσει μόνο σε συνθήκες αραιής ατμόσφαιρας και κενού.
Για τις πρακτικές εφαρμογές των παραπάνω, βλέπε στο ίδιο blog και το άρθρο: https://geometax12.blogspot.com/2021/07/blog-post.html
Μια εναλλακτική προσέγγιση (όχι όμως και φθηνότερη), είναι ο διαστημικός ανελκυστήρας (εικόνα κάτω), που αποτελείται από ένα πολύ ελαφρύ αλλά ισχυρό "σχοινί" που θα εκτείνεται από κάποιο σημείο στη Γη κοντά στον ισημερινό μέχρι αρκετά πάνω από τα 36.000km που είναι το ύψος της γεωσύγχρονης τροχιάς. Και αυτό καθώς στην "επάνω" άκρη του θα έχει προσδεθεί κάτι αρκετά βαρύ (ένας μικρός αστεροειδής πχ) που θα το κρατάει τεντωμένο, ενώ φυσικά θα πρέπει να παραμένει πάντοτε πάνω από το ίδιο σημείο της Γης. Ένα αντικείμενο που βρίσκεται μέχρι το ύψος της γεωσύγχρονης τροχιάς (και κινείται με την ίδια γωνιακή ταχύτητα με τη Γη) θα έχει την τάση να ξαναπέσει στη Γη. Όταν βρίσκεται ακριβώς στη γεωσύγχρονη τροχιά θα μπορεί απλά να παραμένει σε τροχιά στο ίδιο σημείο σε σχέση με τη Γη (όπως οι τηλεπικοινωνιακοί δορυφόροι), ενώ μακρύτερα θα έχει την τάση να απομακρυνθεί από τη Γη. Στην τελευταία αυτή περίπτωση είναι το σχοινί που θα τον συγκρατεί σε κυκλική τροχιά, με αποτέλεσμα να τεντώνεται, επιτρέποντας έτσι σε έναν θαλαμίσκο να κινηθεί κατά μήκος του. Το πρόβλημα είναι ότι το "σχοινί" αυτό, με την τεχνολογία των αρχών της δεκαετίας του 2020, δεν μπορεί ακόμα να κατασκευαστεί. Επιπλέον, χρειάζεται μια κατασκευή μήκους τουλάχιστον 50.000km για να ανεβάσει ανθρώπους ή φορτίο στα 400km περίπου (ύψος του Διεθνούς Διαστημικού Σταθμού).
*θάλαμος, γιατί στη δεύτερη περίπτωση ο όρος «διαστημόπλοιο» είναι μάλλον ευφημισμός.
**Στο ύψος αυτό, οι συγκρούσεις των μορίων του "αέρα" μεταξύ τους είναι σπανιότερες και από το υψηλότερο κενό που μπορεί να δημιουργηθεί σε εργαστήριο στο έδαφος.
Μία άλλη εναλλακτική μέθοδος θέσης σε τροχιά, αλλά για φορτία μόνο μερικών δεκάδων κιλών, έρχεται από την SpinLaunch, μια εταιρεία στην Καλιφόρνια που προτείνει την κατασκευή μιας κατακόρυφης φυγοκέντρου με διάμετρο 100m (εικόνα κάτω), που θα επιταχύνει ένα ωφέλιμο φορτίο 200kg προσαρμοσμένο στην άκρη ενός πολύ αεροδυναμικού και συμπαγούς πυραύλου, σε στροφές που θα το υποβάλουν σε περίπου 10.000g (g: τιμή της γήινης επιτάχυνση). Η όλη διαδικασία θα γίνεται σε κενό και την κατάλληλη στιγμή το φορτίο με τον πύραυλο θα απελευθερώνεται, θα σπάει έναν δίσκο που θα φράζει την έξοδο και θα εκτοξεύεται κατακόρυφα με ταχύτητα που θα πλησιάζει τα 8000km/h. Η αρχική ώθηση θα ανεβάζει τη βολίδα μέχρι τα 60km, οπότε μετά θα αναλαμβάνει ο πύραυλος για να συμπληρώσει το υψόμετρο ώστε να τεθεί το φορτίο σε τροχιά. Μπορεί να ακούγεται σαν μία ενεργειακά οικονομική λύση, αλλά η αρχική εκτόξευση θα παρέχει μόνο το 10% περίπου της συνολικής ενέργειας που απαιτείται, ενώ η υπόλοιπη θα προέρχεται από τον πύραυλο. Θα πρέπει επίσης να αντιμετωπιστεί η υπερθέρμανση εξαιτίας της πολύ υψηλής αρχικής ταχύτητας καθώς και οι κραδασμοί του μηχανισμού φυγοκέντρισης αμέσως μετά την απελευθέρωση της βολίδας.
97. Γιατί απωθούνται τα ομώνυμα και έλκονται τα ετερώνυμα φορτία;
Η δυσκολία κατανόησης ξεκινάει από το γεγονός ότι φανταζόμαστε τα θετικά και τα αρνητικά φορτία να προσδίδουν αντίθετες ιδιότητες στην ύλη, ενώ τα φαινόμενα θα γίνονταν πιο εύκολα κατανοητά (στην ουσία τους) αν σκεφτόμασταν τα αρνητικά φορτία σαν ένα πλεόνασμα ελεύθερων ηλεκτρονίων, ενώ τα θετικά σαν έλλειμμα ελεύθερων ηλεκτρονίων, σε σχέση πάντα με την κανονική κατάσταση της ύλης.
Έτσι, καθώς δύο σώματα που φέρουν αντίθετα φορτία πλησιάζουν μεταξύ τους, δημιουργείται ένα ολοένα και ισχυρότερο ηλεκτρικό πεδίο, οπότε για να επέλθει ισορροπία (κάθε πεδίο είναι μία διαταραχή στον χώρο) η καλύτερη λύση είναι το άγγιγμα των φορτισμένων σωμάτων μεταξύ τους, ώστε τα φορτία να μοιραστούν.
Αυτό σχετίζεται με την γενική αρχή της Φύσης, σύμφωνα με την οποία τα φαινόμενα τείνουν προς την αύξηση της εντροπίας ενός συστήματος, δηλαδή την ομοιόμορφη διασπορά των αιτίων που δημιουργούν τα φαινόμενα, κάτι που οδηγεί σε μεγαλύτερη σταθερότητα (για την Εντροπία βλ. και το θέμα Νο 53).
Αντίθετα, όταν τα σώματα έχουν και τα δύο είτε περίσσεια είτε έλλειψη ηλεκτρονίων, η μόνη λύση είναι να απομακρυνθούν το ένα από το άλλο, έτσι ώστε να εξασθενίσει το μεταξύ τους ηλεκτρικό πεδίο.
Με τους μαγνήτες συμβαίνει κάτι αντίστοιχο. Οι μαγνήτες δεν βασίζονται στα ελεύθερα ηλεκτρόνια, αλλά η γενική αρχή της τάσης της μείωσης του μαγνητικού (σ’ αυτή την περίπτωση) πεδίου, παραμένει. Έτσι, όταν ένας μαγνήτης πλησιάσει έναν άλλον, παίρνει τέτοια θέση ώστε οι αντίθετοι πόλοι να πλησιάσουν, κάτι που μειώνει τοπικά την ένταση του μαγνητικού πεδίου.
Ο πρώτος, είναι ο διάσημος τύπος του Αϊνστάιν για την ισοδυναμία της ύλης με την ενέργεια, ο δεύτερος είναι γνωστός από τη Γυμνασιακή Φυσική και εκφράζει την κινητική ενέργεια ενός σώματος.
Με μια πρώτη ματιά φαίνεται ότι οι δύο τύποι έχουν πολύ παρόμοια δομή και μοιάζει σαν ο πρώτος τύπος να δίνει απλά τη διπλάσια ενέργεια από την κινητική ενός σώματος, όταν αυτό κινείται με την ταχύτητα του φωτός.
Η ομοιότητα αυτή όμως είναι απατηλή, καθώς ο πρώτος τύπος εκφράζει την ενέργεια που περιέχεται σε μία μάζα σε ηρεμία, εφόσον η μάζα αυτή μετατραπεί πλήρως σε ενέργεια.
Όμως αυτή η εξήγηση δεν ανταποκρίνεται πλήρως στην πραγματικότητα, και αυτό γίνεται καλύτερα κατανοητό αν θεωρήσουμε την ύλη σαν «συμπυκνωμένη» ενέργεια. Έτσι, αυτό που συμβαίνει σε μία πυρηνική αντίδραση είναι ότι γίνεται αναδιάταξη της ενέργειας που αποτελεί την ίδια την αρχική ύλη, και κατά την πορεία αυτής της μετατροπής σε μία άλλη διάταξη (που είναι τα προϊόντα), προκύπτει διαφορά ενέργειας η οποία ελευθερώνεται στο περιβάλλον. Πηγαίνοντας τώρα ανάποδα, μπορούμε να αντιστοιχήσουμε την ενέργεια αυτή σε «ύλη» που εξαφανίσθηκε.
Όσο για τον δεύτερο τύπο, αυτός εκφράζει την κινητική ενέργεια ενός σώματος που μετατοπίζεται μέσα στα όρια της καθημερινής (Νευτώνιας) Φυσικής, και φυσικά η μάζα του κάθε άλλο παρά χάνεται, το πολύ-πολύ να χωριστεί σε κομμάτια μετά από μια σφοδρή σύγκρουση.
Για να δούμε τώρα πώς εφαρμόζεται ο πρώτος τύπος, στην περίπτωση της πυρηνικής σχάσης.
Όπως είναι γνωστό, μια κλασική πυρηνική βόμβα σχάσης ουρανίου (όπως αυτή που έπεσε στη Χιροσίμα) εκρήγνυται όταν δύο κομμάτια ουρανίου U-235 καθαρότητας τουλάχιστον 90%, ενωθούν ισχυρά ώστε να αποτελέσουν μία ενιαία συμπαγή μάζα, μεγαλύτερη από την κρίσιμη μάζα που απαιτείται για να ξεκινήσει η αλυσιδωτή αντίδραση. Η αντίδραση αυτή παράγει προϊόντα μεταστοιχείωσης (δηλαδή διαφορετικά στοιχεία από αυτά που συμμετείχαν αρχικά στην αντίδραση) τα οποία έχουν συνολικά λίγο μικρότερη μάζα από τη αρχική. Η μάζα που «λείπει» αντιστοιχεί στην ενέργεια που απελευθερώθηκε, όπως εξηγήθηκε παραπάνω.
Υπάρχει όμως ένα πρόβλημα, (ή μάλλον δύο) που εμποδίζουν το μεγαλύτερο μέρος του σχάσιμου υλικού να συμμετέχει στη σχάση.
Οι λόγοι είναι ότι τόσο η παραγωγή προϊόντων μεταστοιχείωσης όσο και ο μηχανικός κατακερματισμός του σχάσιμου υλικού καθώς ξεκινά να εκρήγνυται, διακόπτουν την αλυσιδωτή αντίδραση καθώς δεν υπάρχει πλέον ενιαία μάζα σχάσιμου υλικού μεγαλύτερη από την κρίσιμη ποσότητα. Γι' αυτό πρακτικά ένας πυρηνικός αντιδραστήρας δεν μπορεί να καταλήξει σε ατομική βόμβα. Η ίδια η αρχή της έκρηξης σταματάει την εξέλιξή της, εκτός αν το πυρηνικό υλικό συνενωθεί και διατηρηθεί κάτω από τεράστια πίεση.
Συγκεκριμένα, στην περίπτωση της βόμβας της Χιροσίμα, εκτιμάται ότι από τα συνολικά 64kg ουρανίου U-235 που περιείχε, μόνον 1kg περίπου συμμετείχε στη σχάση, αλλά και από αυτό μόνο το ισοδύναμο 1g μετατράπηκε τελικά σε ενέργεια. Μάλιστα, για την παραγωγή των 64 αυτών κιλών ουρανίου, χρειάστηκε να εμπλουτιστούν 10t φυσικού ουρανίου (βασικά ουρανίου U-238) στο οποίο το σχάσιμο U-235 περιέχεται σε ποσοστό μικρότερο από 1%.
Ακόμα, πολλαπλάσια των 10t ποσότητα του ορυκτού πισουρανίτη έπρεπε προηγουμένως να εξορυχθεί και να υποστεί βασική κατεργασία, ώστε να καταλήξει σε φυσικό ουράνιο.
Πολύ καλύτερη απόδοση επιτυγχάνεται με τη χρήση πλουτωνίου για τη σχάση (παραγόμενο από U-238 μέσα σε πυρηνικούς αντιδραστήρες), οπότε η δεύτερη βόμβα που έπεσε λίγο αργότερα στο Ναγκασάκι, είχε κατασκευαστεί με πλουτώνιο και αρκετά διαφορετική τεχνολογία.
Ο στόχος (κυριολεκτικά) του ελεύθερου σκοπευτή στον στρατό είναι να εξουδετερώνει ανθρώπινους στόχους «αξίας» από μεγάλη απόσταση, με μία βολή και χωρίς να γίνεται αντιληπτός. Προφανώς πρέπει να είναι άριστος σκοπευτής, με πλήρη γνώση των βλητικών χαρακτηριστικών του συνδυασμού όπλου - πυρομαχικών του, και με την ικανότητα να μένει ακίνητος για πολλές ώρες γινόμενος "ένα" με το περιβάλλον.
Όταν όμως η βολή είναι ιδιαίτερα μακρινή, σε αποστάσεις που πλησιάζουν ή και υπερβαίνουν το ένα χιλιόμετρο (γίνονται και επιτυχείς βολές κοντά στα δύο χιλιόμετρα, με τη μακρύτερη καταγεγραμμένη στα 3.5km), υπάρχουν ιδιαίτερα θέματα Φυσικής που πρέπει να λαμβάνονται υπόψη.
Οι προφανείς δύο παράγοντες είναι η βαρύτητα και ο άνεμος, που η πρώτη εκτρέπει τη βολίδα προς τα κάτω και ο δεύτερος προς το πλάι.
Στις μεγάλες αποστάσεις όμως, τα πράγματα γίνονται ακόμα πιο πολύπλοκα. Κατ’ αρχήν ο άνεμος σπάνια θα είναι ακριβώς κάθετος στην τροχιά της βολίδας, άρα θα υπάρχει πάντα μία συνιστώσα που είτε θα σπρώχνει τη βολίδα προς τον στόχο είτε θα τη φρενάρει, σε σχέση φυσικά με τον ακίνητο αέρα. Και παρόλο που η απόσταση προς τον στόχο μπορεί να μετρηθεί με ακρίβεια με οπτικό τρόπο (συνήθως από τον συνεργάτη του σκοπευτή), η πτώση της βολίδας στο κατακόρυφο επίπεδο εξαρτάται τόσο από την κατά μήκος συνιστώσα του ανέμου αλλά και από την πίεση, θερμοκρασία και υγρασία του αέρα!
Και δεν είναι μόνο αυτό. Επειδή η βολίδα περιστρέφεται ταχύτατα κατά την πορεία της (εξαιτίας των ραβδώσεων της κάνης), αναπτύσσεται ισχυρό γυροσκοπικό φαινόμενο που τη διατηρεί παράλληλη με την κάνη κατά την τροχιά της. Καθώς όμως η βολίδα αρχίζει να χάνει ύψος, παραμένοντας πάντα παράλληλη με την κάνη, συναντά τον αέρα υπό κάποια γωνία (από εμπρός και κάτω) και όχι ακριβώς κατά τον άξονά της. Ο «φαινόμενος» αυτός άνεμος σπρώχνει τη μύτη της βολίδας προς τα επάνω, αλλά εξαιτίας του φαινομένου της γυροσκοπικής μετάπτωσης η βολίδα γυρίζει (ελάχιστα βέβαια) προς το πλάι. Η θέση αυτή όμως προβάλει μέρος της πλευρικής επιφάνειας στον φαινόμενο άνεμο, με αποτέλεσμα να σπρωχτεί λίγο προς το πλάι της αρχικής τροχιάς της*.
Και δεν είναι μόνο τα παραπάνω, καθώς εδώ υπεισέρχεται πλέον και η περιστροφή της Γης, με τη μορφή των επιδράσεων Coriolis και Eötvös (από τα ονόματα των ανθρώπων που εξήγησαν για πρώτη φορά τα αντίστοιχα φαινόμενα).
Η επίδραση Coriolis αφορά την προς το πλάι μετακίνηση ενός βλήματος που κινείται στον άξονα Βορρά - Νότου (ή έχει κάποια συνιστώσα της κίνησής του στον άξονα αυτόν) και οφείλεται στο ότι περιοχές με διαφορετικό γεωγραφικό πλάτος επάνω στη Γη έχουν διαφορετικές γραμμικές ταχύτητες εξαιτίας της περιστροφής της Γης. Και μάλιστα όσο πιο κοντά στους Πόλους βρίσκονται τα σημεία αυτά, τόσο η επίδραση είναι εντονότερη.
Αντίστοιχα, η επίδραση Eötvös εμφανίζεται κατά την κίνηση στον άξονα Ανατολής –Δύσης, και η επίδραση είναι πιο έντονη κοντά στον Ισημερινό. Οφείλεται στη διαφορά ταχύτητας του βλήματος σε σχέση με τη γραμμική της Γης στο συγκεκριμένο γεωγραφικό πλάτος, καθώς αν το βλήμα κινείται ανατολικά το βάρος του φαίνεται να μειώνεται, ενώ προς τα δυτικά το βάρος του φαίνεται να αυξάνεται. Η εξήγηση είναι ότι το βάρος ενός σώματος είναι ίσο με την έλξη της Γης μείον τη «φυγόκεντρο» που δημιουργείται καθώς το σώμα αυτό περιστρέφεται γύρω της, αφού η δύναμη αυτή (στην ουσία η αντίδραση στην κεντρομόλο) προσπαθεί να το απομακρύνει απ’ αυτήν. Έτσι κινούμενο ανατολικά στην ταχύτητά του προστίθεται η ταχύτητα περιστροφής της Γης, ενώ κινούμενο δυτικά αφαιρείται. (Για τον ίδιο λόγο οι πύραυλοι μπαίνουν σε τροχιά κινούμενοι ανατολικά).
Ίσως οι επιδράσεις Coriolis και Eötvös να μοιάζουν αμελητέες, όμως σε αποστάσεις της τάξης του ενός χιλιομέτρου ήδη εκτρέπουν τη βολίδα του ελεύθερου σκοπευτή κατά μερικά εκατοστά, αρκετά για να κάνουν τη διαφορά της επιτυχίας από την αποτυχία. Ειδικά όταν δεν υπάρχει περιθώριο για προηγούμενες βολές ρύθμισης, ούτε για επόμενες σε περίπτωση αποτυχίας.
Ίσως το ερώτημα θα έπρεπε να ήταν, γιατί όλα τα υλικά δεν είναι διάφανα; Και αυτό επειδή, η κλασική θεώρηση των μορίων και των ατόμων τα παρουσιάζει να έχουν έναν μικροσκοπικό σφαιρικό πυρήνα με έναν τεράστιο άδειο χώρο γύρω τους, στον οποίο περιστρέφονται (σαν πλανήτες γύρω από τον ήλιο) μερικά ελάχιστα σε μέγεθος ηλεκτρόνια. Μια συνηθισμένη αναλογία είναι σαν να υπάρχει ένα ρεβίθι στη «σέντρα» ενός γηπέδου ποδοσφαίρου (ο πυρήνας) και στις κερκίδες να κινούνται μερικοί κόκκοι άμμου, τα ηλεκτρόνια.
Ένα (ακόμα) παράδοξο που συνδέεται με το γυαλί είναι το φαινόμενο που ονομάζεται "Η σταγόνα του πρίγκιπα Ρούπερτ", γνωστό από τον 17ο αι. (εικόνα επάνω). Το σχήμα αυτό προκύπτει από την απότομη ψύξη μας σταγόνας λιωμένου γυαλιού που πέφτει μέσα σε κρύο νερό, αφήνοντας πίσω της μια λεπτή γυάλινη "ουρά". Και ενώ η "κεφαλή" της σταγόνας έχει πολύ μεγάλη αντοχή σε χτυπήματα, η "ουρά" είναι εύθραυστη, και μάλιστα όταν σπάσει προκαλεί ένα εσωτερικό ταχύτατο κύμα που φτάνει και διαλύει μέχρι και την πολύ ανθεκτική κεφαλή. Το φαινόμενο αποδίδεται στον βραδύτερο ρυθμό ψύξης της κεφαλής που την κάνει πολύ ανθεκτική σε εξωτερικά χτυπήματα, αλλά εύθραυστη σε εσωτερικά.
Με μια πρώτη ματιά φαίνεται ότι οι δύο τύποι έχουν πολύ παρόμοια δομή και μοιάζει σαν ο πρώτος τύπος να δίνει απλά τη διπλάσια ενέργεια από την κινητική ενός σώματος, όταν αυτό κινείται με την ταχύτητα του φωτός.
Η ομοιότητα αυτή όμως είναι απατηλή, καθώς ο πρώτος τύπος εκφράζει την ενέργεια που περιέχεται σε μία μάζα σε ηρεμία, εφόσον η μάζα αυτή μετατραπεί πλήρως σε ενέργεια.
Όμως αυτή η εξήγηση δεν ανταποκρίνεται πλήρως στην πραγματικότητα, και αυτό γίνεται καλύτερα κατανοητό αν θεωρήσουμε την ύλη σαν «συμπυκνωμένη» ενέργεια. Έτσι, αυτό που συμβαίνει σε μία πυρηνική αντίδραση είναι ότι γίνεται αναδιάταξη της ενέργειας που αποτελεί την ίδια την αρχική ύλη, και κατά την πορεία αυτής της μετατροπής σε μία άλλη διάταξη (που είναι τα προϊόντα), προκύπτει διαφορά ενέργειας η οποία ελευθερώνεται στο περιβάλλον. Πηγαίνοντας τώρα ανάποδα, μπορούμε να αντιστοιχήσουμε την ενέργεια αυτή σε «ύλη» που εξαφανίσθηκε.
Όσο για τον δεύτερο τύπο, αυτός εκφράζει την κινητική ενέργεια ενός σώματος που μετατοπίζεται μέσα στα όρια της καθημερινής (Νευτώνιας) Φυσικής, και φυσικά η μάζα του κάθε άλλο παρά χάνεται, το πολύ-πολύ να χωριστεί σε κομμάτια μετά από μια σφοδρή σύγκρουση.
Για να δούμε τώρα πώς εφαρμόζεται ο πρώτος τύπος, στην περίπτωση της πυρηνικής σχάσης.
Όπως είναι γνωστό, μια κλασική πυρηνική βόμβα σχάσης ουρανίου (όπως αυτή που έπεσε στη Χιροσίμα) εκρήγνυται όταν δύο κομμάτια ουρανίου U-235 καθαρότητας τουλάχιστον 90%, ενωθούν ισχυρά ώστε να αποτελέσουν μία ενιαία συμπαγή μάζα, μεγαλύτερη από την κρίσιμη μάζα που απαιτείται για να ξεκινήσει η αλυσιδωτή αντίδραση. Η αντίδραση αυτή παράγει προϊόντα μεταστοιχείωσης (δηλαδή διαφορετικά στοιχεία από αυτά που συμμετείχαν αρχικά στην αντίδραση) τα οποία έχουν συνολικά λίγο μικρότερη μάζα από τη αρχική. Η μάζα που «λείπει» αντιστοιχεί στην ενέργεια που απελευθερώθηκε, όπως εξηγήθηκε παραπάνω.
Υπάρχει όμως ένα πρόβλημα, (ή μάλλον δύο) που εμποδίζουν το μεγαλύτερο μέρος του σχάσιμου υλικού να συμμετέχει στη σχάση.
Οι λόγοι είναι ότι τόσο η παραγωγή προϊόντων μεταστοιχείωσης όσο και ο μηχανικός κατακερματισμός του σχάσιμου υλικού καθώς ξεκινά να εκρήγνυται, διακόπτουν την αλυσιδωτή αντίδραση καθώς δεν υπάρχει πλέον ενιαία μάζα σχάσιμου υλικού μεγαλύτερη από την κρίσιμη ποσότητα. Γι' αυτό πρακτικά ένας πυρηνικός αντιδραστήρας δεν μπορεί να καταλήξει σε ατομική βόμβα. Η ίδια η αρχή της έκρηξης σταματάει την εξέλιξή της, εκτός αν το πυρηνικό υλικό συνενωθεί και διατηρηθεί κάτω από τεράστια πίεση.
Συγκεκριμένα, στην περίπτωση της βόμβας της Χιροσίμα, εκτιμάται ότι από τα συνολικά 64kg ουρανίου U-235 που περιείχε, μόνον 1kg περίπου συμμετείχε στη σχάση, αλλά και από αυτό μόνο το ισοδύναμο 1g μετατράπηκε τελικά σε ενέργεια. Μάλιστα, για την παραγωγή των 64 αυτών κιλών ουρανίου, χρειάστηκε να εμπλουτιστούν 10t φυσικού ουρανίου (βασικά ουρανίου U-238) στο οποίο το σχάσιμο U-235 περιέχεται σε ποσοστό μικρότερο από 1%.
Ακόμα, πολλαπλάσια των 10t ποσότητα του ορυκτού πισουρανίτη έπρεπε προηγουμένως να εξορυχθεί και να υποστεί βασική κατεργασία, ώστε να καταλήξει σε φυσικό ουράνιο.
Πολύ καλύτερη απόδοση επιτυγχάνεται με τη χρήση πλουτωνίου για τη σχάση (παραγόμενο από U-238 μέσα σε πυρηνικούς αντιδραστήρες), οπότε η δεύτερη βόμβα που έπεσε λίγο αργότερα στο Ναγκασάκι, είχε κατασκευαστεί με πλουτώνιο και αρκετά διαφορετική τεχνολογία.
99. Η πολύπλοκη Φυσική των ελεύθερων σκοπευτών.
Όταν όμως η βολή είναι ιδιαίτερα μακρινή, σε αποστάσεις που πλησιάζουν ή και υπερβαίνουν το ένα χιλιόμετρο (γίνονται και επιτυχείς βολές κοντά στα δύο χιλιόμετρα, με τη μακρύτερη καταγεγραμμένη στα 3.5km), υπάρχουν ιδιαίτερα θέματα Φυσικής που πρέπει να λαμβάνονται υπόψη.
Οι προφανείς δύο παράγοντες είναι η βαρύτητα και ο άνεμος, που η πρώτη εκτρέπει τη βολίδα προς τα κάτω και ο δεύτερος προς το πλάι.
Στις μεγάλες αποστάσεις όμως, τα πράγματα γίνονται ακόμα πιο πολύπλοκα. Κατ’ αρχήν ο άνεμος σπάνια θα είναι ακριβώς κάθετος στην τροχιά της βολίδας, άρα θα υπάρχει πάντα μία συνιστώσα που είτε θα σπρώχνει τη βολίδα προς τον στόχο είτε θα τη φρενάρει, σε σχέση φυσικά με τον ακίνητο αέρα. Και παρόλο που η απόσταση προς τον στόχο μπορεί να μετρηθεί με ακρίβεια με οπτικό τρόπο (συνήθως από τον συνεργάτη του σκοπευτή), η πτώση της βολίδας στο κατακόρυφο επίπεδο εξαρτάται τόσο από την κατά μήκος συνιστώσα του ανέμου αλλά και από την πίεση, θερμοκρασία και υγρασία του αέρα!
Και δεν είναι μόνο αυτό. Επειδή η βολίδα περιστρέφεται ταχύτατα κατά την πορεία της (εξαιτίας των ραβδώσεων της κάνης), αναπτύσσεται ισχυρό γυροσκοπικό φαινόμενο που τη διατηρεί παράλληλη με την κάνη κατά την τροχιά της. Καθώς όμως η βολίδα αρχίζει να χάνει ύψος, παραμένοντας πάντα παράλληλη με την κάνη, συναντά τον αέρα υπό κάποια γωνία (από εμπρός και κάτω) και όχι ακριβώς κατά τον άξονά της. Ο «φαινόμενος» αυτός άνεμος σπρώχνει τη μύτη της βολίδας προς τα επάνω, αλλά εξαιτίας του φαινομένου της γυροσκοπικής μετάπτωσης η βολίδα γυρίζει (ελάχιστα βέβαια) προς το πλάι. Η θέση αυτή όμως προβάλει μέρος της πλευρικής επιφάνειας στον φαινόμενο άνεμο, με αποτέλεσμα να σπρωχτεί λίγο προς το πλάι της αρχικής τροχιάς της*.
Και δεν είναι μόνο τα παραπάνω, καθώς εδώ υπεισέρχεται πλέον και η περιστροφή της Γης, με τη μορφή των επιδράσεων Coriolis και Eötvös (από τα ονόματα των ανθρώπων που εξήγησαν για πρώτη φορά τα αντίστοιχα φαινόμενα).
Η επίδραση Coriolis αφορά την προς το πλάι μετακίνηση ενός βλήματος που κινείται στον άξονα Βορρά - Νότου (ή έχει κάποια συνιστώσα της κίνησής του στον άξονα αυτόν) και οφείλεται στο ότι περιοχές με διαφορετικό γεωγραφικό πλάτος επάνω στη Γη έχουν διαφορετικές γραμμικές ταχύτητες εξαιτίας της περιστροφής της Γης. Και μάλιστα όσο πιο κοντά στους Πόλους βρίσκονται τα σημεία αυτά, τόσο η επίδραση είναι εντονότερη.
Αντίστοιχα, η επίδραση Eötvös εμφανίζεται κατά την κίνηση στον άξονα Ανατολής –Δύσης, και η επίδραση είναι πιο έντονη κοντά στον Ισημερινό. Οφείλεται στη διαφορά ταχύτητας του βλήματος σε σχέση με τη γραμμική της Γης στο συγκεκριμένο γεωγραφικό πλάτος, καθώς αν το βλήμα κινείται ανατολικά το βάρος του φαίνεται να μειώνεται, ενώ προς τα δυτικά το βάρος του φαίνεται να αυξάνεται. Η εξήγηση είναι ότι το βάρος ενός σώματος είναι ίσο με την έλξη της Γης μείον τη «φυγόκεντρο» που δημιουργείται καθώς το σώμα αυτό περιστρέφεται γύρω της, αφού η δύναμη αυτή (στην ουσία η αντίδραση στην κεντρομόλο) προσπαθεί να το απομακρύνει απ’ αυτήν. Έτσι κινούμενο ανατολικά στην ταχύτητά του προστίθεται η ταχύτητα περιστροφής της Γης, ενώ κινούμενο δυτικά αφαιρείται. (Για τον ίδιο λόγο οι πύραυλοι μπαίνουν σε τροχιά κινούμενοι ανατολικά).
Ίσως οι επιδράσεις Coriolis και Eötvös να μοιάζουν αμελητέες, όμως σε αποστάσεις της τάξης του ενός χιλιομέτρου ήδη εκτρέπουν τη βολίδα του ελεύθερου σκοπευτή κατά μερικά εκατοστά, αρκετά για να κάνουν τη διαφορά της επιτυχίας από την αποτυχία. Ειδικά όταν δεν υπάρχει περιθώριο για προηγούμενες βολές ρύθμισης, ούτε για επόμενες σε περίπτωση αποτυχίας.
ΥΓ. Η άκρη της κάνης είναι πολύ σημαντικό να μην έχει κάποια χαρακιά ή την παραμικρή φθορά, γιατί αν τα αέρια που ξεκινούν να διαφεύγουν μόλις το βλήμα εγκαταλείψει την κάνη δεν το κάνουν με απολύτως συμμετρικό τρόπο, ασκούνται πλάγιες δυνάμεις στη βάση του βλήματος που επηρεάζουν την τροχιά του.
*Ο προσεκτικός αναγνώστης θα αναρωτηθεί εάν ο πλευρικός άνεμος προκαλεί ενδεχομένως και το φαινόμενο Magnus καθώς η βολίδα περιστρέφεται (όπως γίνεται για παράδειγμα με τα «φάλτσα» στις μπάλες του ποδοσφαίρου και του τένις). Πράγματι το φαινόμενο υπάρχει, αλλά για τις αποστάσεις (και τον χρόνο πτήσης) της βολίδας του ελεύθερου σκοπευτή είναι αμελητέο. Λαμβάνεται όπως υπόψη στα βλήματα του πυροβολικού, που βρίσκονται στον αέρα για πολύ μεγαλύτερο χρόνο.
100. Γιατί το γυαλί είναι διάφανο;
*Ο προσεκτικός αναγνώστης θα αναρωτηθεί εάν ο πλευρικός άνεμος προκαλεί ενδεχομένως και το φαινόμενο Magnus καθώς η βολίδα περιστρέφεται (όπως γίνεται για παράδειγμα με τα «φάλτσα» στις μπάλες του ποδοσφαίρου και του τένις). Πράγματι το φαινόμενο υπάρχει, αλλά για τις αποστάσεις (και τον χρόνο πτήσης) της βολίδας του ελεύθερου σκοπευτή είναι αμελητέο. Λαμβάνεται όπως υπόψη στα βλήματα του πυροβολικού, που βρίσκονται στον αέρα για πολύ μεγαλύτερο χρόνο.
100. Γιατί το γυαλί είναι διάφανο;
Στην πραγματικότητα όμως (τουλάχιστον στην «πραγματικότητα» της κβαντομηχανικής), τα ηλεκτρόνια βρίσκονται «παντού και πουθενά», οπότε φαίνεται ότι όλος ο όγκος του γηπέδου να είναι κατειλημμένος από το πεδίο που δημιουργεί η κίνηση των ηλεκτρονίων.
Τότε γιατί το γυαλί αποτελεί εξαίρεση και είναι διάφανο;
Επειδή, για να εξαφανιστεί ένα φωτόνιο πρέπει κάποιο ηλεκτρόνιο να μπορεί να το απορροφήσει (αλλάζοντας προσωρινά ενεργειακή κατάσταση και τροχιά) και αυτό είναι κάτι που τα άμορφα υλικά (που είναι συνήθως υγρά και αέρια) δεν μπορούν να το κάνουν, γιατί δεν διαθέτουν κατάλληλη ενεργειακή τροχιά για τα ηλεκτρόνιά τους.
Τότε γιατί το γυαλί αποτελεί εξαίρεση και είναι διάφανο;
Επειδή, για να εξαφανιστεί ένα φωτόνιο πρέπει κάποιο ηλεκτρόνιο να μπορεί να το απορροφήσει (αλλάζοντας προσωρινά ενεργειακή κατάσταση και τροχιά) και αυτό είναι κάτι που τα άμορφα υλικά (που είναι συνήθως υγρά και αέρια) δεν μπορούν να το κάνουν, γιατί δεν διαθέτουν κατάλληλη ενεργειακή τροχιά για τα ηλεκτρόνιά τους.
Το γυαλί είναι ουσιαστικά το μόνο άμορφο ανάμεσα στα στερεά υλικά, αλλά και πάλι η άρνησή του να απορροφήσει φωτόνια αφορά μόνο στα φωτόνια του ορατού φάσματος, ενώ αντίθετα απορροφά τα φωτόνια του υπεριώδους φάσματος, όπως ξέρουν (ή θα έπρεπε να ξέρουν) όσοι προσπάθησαν να κάνουν ηλιοθεραπεία πίσω από κοινό τζάμι.
Επιπλέον, πολλά στερεά υλικά είναι διαπερατά από φωτόνια πολύ μεγαλύτερης ενέργειας από του ορατού φωτός, γι’ αυτό και οι μαλακοί ιστοί του σώματος είναι διαφανείς στις ακτίνες Χ.
Επιπλέον, πολλά στερεά υλικά είναι διαπερατά από φωτόνια πολύ μεγαλύτερης ενέργειας από του ορατού φωτός, γι’ αυτό και οι μαλακοί ιστοί του σώματος είναι διαφανείς στις ακτίνες Χ.
ΥΓ. Και όμως υπάρχει τρόπος να κάνουμε το γυαλί αδιάφανο "κατά παραγγελία", με μια μέθοδο που βρέθηκε τη δεκαετία του '80, και συνήθως κυκλοφορεί με το όνομα smart glass.
που ο προσανατολισμός τους αλλάζει με την εφαρμογή τάσης, με τρόπο ώστε να μην εμποδίζεται η διέλευση του φωτός. Το ενδιαφέρον είναι ότι το σύστημα είναι "ασφαλές", με την έννοια ότι συνήθως θέλουμε την αδιαφανή κατάσταση σε ενδεχόμενη διακοπή του ρεύματος.
Μια "παιχνιδιάρικη" χρήση της τεχνολογίας αυτής είναι σε τουαλέτες σε δημόσιους χώρους, που έχουν διάφανους γυάλινους τοίχους, οι οποίοι όμως γίνονται αδιαφανείς μόλις γυρίσει το μάνταλο που τις κλειδώνει.
Για τις πολύ χαμηλές τιμές αντίστασης, όπως προαναφέρθηκε, χρησιμοποιείται μια «γέφυρα», δηλαδή ένα ηλεκτρικό κύκλωμα όπου η άγνωστη αντίσταση (Q) συγκρίνεται με μία ρυθμιζόμενη γνωστή αντίσταση (S), (εικόνα κάτω).
Το όργανο μέτρησης δείχνει ακριβώς τη στιγμή που επέρχεται η ισορροπία ανάμεσα στα δύο κυκλώματα, κάτι που είναι πολύ εύκολο να διαπιστωθεί με μεγάλη ακρίβεια, καθώς συμβαίνει όταν η ένταση μηδενίζεται.
Για τις μεσαίες τιμές αντίστασης, απλά εφαρμόζεται μια σταθερή τάση και το όργανο στην ουσία δείχνει το ρεύμα που περνάει (εικόνα κάτω).
Το όργανο όμως είναι βαθμονομημένο σε Ώμ (Ohm) μετά από δοκιμές, οπότε στην ουσία διαβάζουμε κατευθείαν την τιμή της αντίστασης.
Μέχρι εδώ όλα πάνε καλά, αλλά όσο αυξάνεται η τάση που εφαρμόζεται σε μια αντίσταση, η τιμή της παύει να εμφανίζει γραμμικότητα. Αυτό συμβαίνει επειδή σε μεγαλύτερες τάσεις παρουσιάζονται φαινόμενα εκκενώσεων, επιφανειακών διαρροών, διασπάσεων διακένων, κλπ, και ο νόμος του Ωμ (R=V/I) δεν μπορεί να εφαρμοστεί αξιόπιστα με τη μικρή μπαταρία (συνήθως 1.5V) ενός ωμόμετρου.
Στην περίπτωση αυτή, θα πρέπει η μέτρηση να γίνει με την εφαρμογή τάσης αντίστοιχης με την τάση λειτουργίας της αντίστασης, και αυτό ακριβώς κάνει η συσκευή με το όνομα megger (εμπορικό όνομα που χαρακτηρίζει πλέον όλες τις συσκευές αυτού του είδους). Στην εικόνα κάτω, συσκευή παλαιότερου τύπου με χειροκίνητο μανιατό (γεννήτρια συνεχούς ρεύματος).
Ο ενδείκτης της συσκευής στην ουσία επηρεάζεται (με ξεχωριστά πηνία) τόσο από την τάση που παράγει η συσκευή* όσο και από την ένταση που διαρρέει την αντίσταση που μετριέται. Η σχέση αυτών των δύο μεγεθών προκαλεί την κατάλληλη εκτροπή της βελόνας.
Η παραπάνω προσομοίωση δείχνει πώς συμπεριφέρεται ένα νεκρό (αλλά φρέσκο, δηλαδή εύκαμπτο) ψάρι, εφόσον πιαστεί μέσα στις δίνες που σχηματίζονται από εμπόδια μέσα σ’ ένα ρεύμα νερού, συνήθως μεγάλες πέτρες σε ποτάμι. Το εκπληκτικό είναι ότι το νεκρό ψάρι φαίνεται να κολυμπάει, και μάλιστα να προωθείται αντίθετα από τη ροή του νερού!
Η εξήγηση είναι ότι οι δίνες που σχηματίζουν τα εμπόδια και η ευκαμψία του ψαριού συνδυάζονται έτσι ώστε το ψάρι να μπει σε μία οριζόντια ταλάντωση, πολύ παρόμοια με αυτή που κάνει όταν κολυμπάει. Το αποτέλεσμα είναι το νεκρό ψάρι να προωθείται ενάντια στο ρεύμα και μάλιστα αν φτάσει στην αρχή της περιοχής δημιουργίας των στροβίλων, μπορεί να παρασυρθεί προς τα πίσω και η διαδικασία να ξεκινήσει από την αρχή.
Προσέξτε στην εικόνα τους «θύλακες» χαμηλής πίεσης που δημιουργούνται από τους στροβίλους (εκεί όπου οι γραμμές της ροής αραιώνουν) και οι οποίοι υποβάλλουν το ψάρι σε εναλλασσόμενη κάμψη. Προφανώς, το φαινόμενο αυτό το διαισθάνονται τα (ζωντανά) ψάρια και το αξιοποιούν, ώστε να προωθούνται χωρίς κόπο ενάντια στο ρεύμα του ποταμού, εφόσον η διαμόρφωση των εμποδίων δημιουργεί τις κατάλληλες συνθήκες.
Ένα σχετικό βίντεο (στα αγγλικά), υπήρχε στη διεύθυνση που σημειώνεται παρακάτω. Η προσομοίωση του νεκρού ψαριού γίνεται προς το τέλος: https://www.fishsens.com/blog/video-shows-how-a-dead-trout-can-swim-upstream/
Και επίσης γνωστό, ότι όταν «λευκό» φως μπαίνει υπό γωνία σε κάποιο οπτικό μέσο και στη συνέχεια βγαίνει απ’ αυτό, εφόσον η επιφάνεια εισόδου είναι παράλληλη με την επιφάνεια εξόδου η δέσμη απλά μετατοπίζεται προς στο πλάι, όπως στην εικόνα 2, χωρίς να αναλύεται στα χρώματα του φάσματος.
101. Τέσσερεις διαφορετικές συσκευές για το ίδιο φυσικό μέγεθος.
Το εν λόγω φυσικό μέγεθος είναι η ωμική αντίσταση, και ανάλογα με την περιοχή που εκτιμάμε ότι βρίσκεται η τιμή της, θα πρέπει να επιλέξουμε:
Το εν λόγω φυσικό μέγεθος είναι η ωμική αντίσταση, και ανάλογα με την περιοχή που εκτιμάμε ότι βρίσκεται η τιμή της, θα πρέπει να επιλέξουμε:
-είτε κάποιου είδους ηλεκτρολογικής «γέφυρας» (η Wheatstone είναι η πιο γνωστή) για πολύ χαμηλές τιμές αντίστασης,
-είτε ένα ωμόμετρο για τη μεσαία περιοχή των τιμών αντίστασης,
-είτε ένα «megger» για τις πολύ ψηλές τιμές, κυρίως σε κυκλώματα που παρεμβάλλονται μονωτικά υλικά και μας ενδιαφέρει ειδικά η διαρροή ρεύματος προς γη,
-είτε ένα όργανο που παράγει μεγάλη ένταση αλλά με χαμηλή τάση, για τις περιπτώσεις μέτρησης αντιστάσεων γείωσης.
Η αρχή της μέτρησης, αν και στη βάση της είναι η ίδια, να εφαρμόζεται δηλαδή μια τάση και να μετριέται το ρεύμα που περνάει, μόνο στην περίπτωση του ωμόμετρου λειτουργεί ακριβώς έτσι.
Για τις πολύ χαμηλές τιμές αντίστασης, όπως προαναφέρθηκε, χρησιμοποιείται μια «γέφυρα», δηλαδή ένα ηλεκτρικό κύκλωμα όπου η άγνωστη αντίσταση (Q) συγκρίνεται με μία ρυθμιζόμενη γνωστή αντίσταση (S), (εικόνα κάτω).
Για τις μεσαίες τιμές αντίστασης, απλά εφαρμόζεται μια σταθερή τάση και το όργανο στην ουσία δείχνει το ρεύμα που περνάει (εικόνα κάτω).
Μέχρι εδώ όλα πάνε καλά, αλλά όσο αυξάνεται η τάση που εφαρμόζεται σε μια αντίσταση, η τιμή της παύει να εμφανίζει γραμμικότητα. Αυτό συμβαίνει επειδή σε μεγαλύτερες τάσεις παρουσιάζονται φαινόμενα εκκενώσεων, επιφανειακών διαρροών, διασπάσεων διακένων, κλπ, και ο νόμος του Ωμ (R=V/I) δεν μπορεί να εφαρμοστεί αξιόπιστα με τη μικρή μπαταρία (συνήθως 1.5V) ενός ωμόμετρου.
Στην περίπτωση αυτή, θα πρέπει η μέτρηση να γίνει με την εφαρμογή τάσης αντίστοιχης με την τάση λειτουργίας της αντίστασης, και αυτό ακριβώς κάνει η συσκευή με το όνομα megger (εμπορικό όνομα που χαρακτηρίζει πλέον όλες τις συσκευές αυτού του είδους). Στην εικόνα κάτω, συσκευή παλαιότερου τύπου με χειροκίνητο μανιατό (γεννήτρια συνεχούς ρεύματος).
Υπάρχει όμως και κάτι άλλο σημαντικό. Επειδή η συσκευή μετράει συνήθως κυκλώματα υψηλής τάσης οπότε θα πρέπει, όπως προαναφέρθηκα, να παράγει την τάση αυτή, η ισχύς των κυκλωμάτων της είναι επίτηδες περιορισμένη ώστε αν κατά λάθος έλθει κάποιος σε επαφή με την τάση αυτή το αποτέλεσμα να μην είναι θανατηφόρο (ή αν η προς μέτρηση αντίσταση είναι τελικά αρκετά χαμηλή, να μην προκληθεί βραχυκύκλωμα).
Κάτι αντίστοιχο συμβαίνει και με το κύκλωμα έναυσης των βενζινοκινητήρων, το οποίο παράγει περίπου 15.000V με αρκετή ισχύ για να δημιουργήσει τον σπινθήρα στην άκρη ενός μπουζί, αλλά όχι για να σκοτώσει έναν άνθρωπο (αν και θα του προκαλέσει ένα ισχυρό σοκ). Το ίδιο ισχύει και για τις συσκευές που χρησιμοποιεί η αστυνομία για την εξουδετέρωση υπόπτων.
Από την άλλη πλευρά, αν θελήσει κάποιος να μετρήσει με megger μια αντίσταση σχετικά χαμηλής τιμής, η μέτρηση μπορεί να τον ξεγελάσει καθώς η συσκευή αυτή είναι ρυθμισμένη να μετράει πολύ υψηλές τιμές (της τάξης των MOhm, δηλαδή εκατομμυρίων Ώμ), οπότε είναι σχετικά «αναίσθητη» σε χαμηλές τιμές αντιστάσεων.
Κάτι αντίστοιχο συμβαίνει και με το κύκλωμα έναυσης των βενζινοκινητήρων, το οποίο παράγει περίπου 15.000V με αρκετή ισχύ για να δημιουργήσει τον σπινθήρα στην άκρη ενός μπουζί, αλλά όχι για να σκοτώσει έναν άνθρωπο (αν και θα του προκαλέσει ένα ισχυρό σοκ). Το ίδιο ισχύει και για τις συσκευές που χρησιμοποιεί η αστυνομία για την εξουδετέρωση υπόπτων.
Από την άλλη πλευρά, αν θελήσει κάποιος να μετρήσει με megger μια αντίσταση σχετικά χαμηλής τιμής, η μέτρηση μπορεί να τον ξεγελάσει καθώς η συσκευή αυτή είναι ρυθμισμένη να μετράει πολύ υψηλές τιμές (της τάξης των MOhm, δηλαδή εκατομμυρίων Ώμ), οπότε είναι σχετικά «αναίσθητη» σε χαμηλές τιμές αντιστάσεων.
*Καθώς η ισχύς της συσκευής είναι περιορισμένη για λόγους ασφαλείας, όταν η ένταση που διαρρέει την προς μέτρηση αντίσταση είναι υψηλή, η τάση "γονατίζει", και αυτό θα πρέπει να λαμβάνεται υπόψη για να παραμένει η ένδειξη σωστή.
Τέλος υπάρχει ένα είδος "αντίστροφου megger", που παράγει δηλαδή σχετικά μεγάλη ένταση υπό χαμηλή τάση, έτσι ώστε να προσομοιάζονται τα ρεύματα των βραχυκυκλωμάτων, οπότε χρησιμοποιείται για τη μέτρηση αντιστάσεων γείωσης (εικόνα κάτω).
Γενικά, μια αντίσταση θα πρέπει να μετριέται κατά το δυνατόν κοντά στα μεγέθη λειτουργίας της (τάσης ή έντασης), αλλά με πολύ περιορισμένη ισχύ ώστε να μην προκληθεί βραχυκύκλωμα ή να κινδυνεύσει ο χειριστής της.
102. Ψάρια ζόμπι!
Η παραπάνω προσομοίωση δείχνει πώς συμπεριφέρεται ένα νεκρό (αλλά φρέσκο, δηλαδή εύκαμπτο) ψάρι, εφόσον πιαστεί μέσα στις δίνες που σχηματίζονται από εμπόδια μέσα σ’ ένα ρεύμα νερού, συνήθως μεγάλες πέτρες σε ποτάμι. Το εκπληκτικό είναι ότι το νεκρό ψάρι φαίνεται να κολυμπάει, και μάλιστα να προωθείται αντίθετα από τη ροή του νερού!
Η εξήγηση είναι ότι οι δίνες που σχηματίζουν τα εμπόδια και η ευκαμψία του ψαριού συνδυάζονται έτσι ώστε το ψάρι να μπει σε μία οριζόντια ταλάντωση, πολύ παρόμοια με αυτή που κάνει όταν κολυμπάει. Το αποτέλεσμα είναι το νεκρό ψάρι να προωθείται ενάντια στο ρεύμα και μάλιστα αν φτάσει στην αρχή της περιοχής δημιουργίας των στροβίλων, μπορεί να παρασυρθεί προς τα πίσω και η διαδικασία να ξεκινήσει από την αρχή.
Προσέξτε στην εικόνα τους «θύλακες» χαμηλής πίεσης που δημιουργούνται από τους στροβίλους (εκεί όπου οι γραμμές της ροής αραιώνουν) και οι οποίοι υποβάλλουν το ψάρι σε εναλλασσόμενη κάμψη. Προφανώς, το φαινόμενο αυτό το διαισθάνονται τα (ζωντανά) ψάρια και το αξιοποιούν, ώστε να προωθούνται χωρίς κόπο ενάντια στο ρεύμα του ποταμού, εφόσον η διαμόρφωση των εμποδίων δημιουργεί τις κατάλληλες συνθήκες.
Ένα σχετικό βίντεο (στα αγγλικά), υπήρχε στη διεύθυνση που σημειώνεται παρακάτω. Η προσομοίωση του νεκρού ψαριού γίνεται προς το τέλος: https://www.fishsens.com/blog/video-shows-how-a-dead-trout-can-swim-upstream/
103. Γιατί συμβαίνει η Διάθλαση;
Η διάθλαση συμβαίνει όταν το φως περνάει από ένα διαφανές μέσο σε κάποιο άλλο επίσης διαφανές, αλλά με διαφορετική «οπτική πυκνότητα» ή σωστότερα διαφορετικό δείκτη διάθλασης, και εφόσον δεν πέφτει τελείως κάθετα στη μεταξύ τους διαχωριστική επιφάνεια.
Η διάθλαση συμβαίνει όταν το φως περνάει από ένα διαφανές μέσο σε κάποιο άλλο επίσης διαφανές, αλλά με διαφορετική «οπτική πυκνότητα» ή σωστότερα διαφορετικό δείκτη διάθλασης, και εφόσον δεν πέφτει τελείως κάθετα στη μεταξύ τους διαχωριστική επιφάνεια.
Εικόνα 1. Η κλασική εικόνα της διάθλασης, με είσοδο / έξοδο σε μη παράλληλα επίπεδα, οπότε τα χρώματα του φάσματος διαχωρίζονται σημαντικά και είναι εύκολο να παρατηρηθούν.
Και επίσης γνωστό, ότι όταν «λευκό» φως μπαίνει υπό γωνία σε κάποιο οπτικό μέσο και στη συνέχεια βγαίνει απ’ αυτό, εφόσον η επιφάνεια εισόδου είναι παράλληλη με την επιφάνεια εξόδου η δέσμη απλά μετατοπίζεται προς στο πλάι, όπως στην εικόνα 2, χωρίς να αναλύεται στα χρώματα του φάσματος.
Εικόνα 2.
Θα αναρωτηθεί όμως κάποιος: Αν το φως μπαίνοντας στο νέο υλικό υπό γωνία αρχίζει να αναλύεται στα χρώματα του φάσματος, όπως φαίνεται στην εικόνα 1, πώς ξανασυντίθεται σε λευκό φως βγαίνοντας από την άλλη παράλληλη επιφάνεια; Η απάντηση είναι, ότι ουσιαστικά δεν ξανασυντίθεται!
Ας παρακολουθήσουμε τι συμβαίνει, στην εικόνα 3.
Θα αναρωτηθεί όμως κάποιος: Αν το φως μπαίνοντας στο νέο υλικό υπό γωνία αρχίζει να αναλύεται στα χρώματα του φάσματος, όπως φαίνεται στην εικόνα 1, πώς ξανασυντίθεται σε λευκό φως βγαίνοντας από την άλλη παράλληλη επιφάνεια; Η απάντηση είναι, ότι ουσιαστικά δεν ξανασυντίθεται!
Ας παρακολουθήσουμε τι συμβαίνει, στην εικόνα 3.
Εικόνα 3.
Μπαίνοντας το λευκό φως (μαύρο στο σχέδιο για πρακτικούς λόγους) λοξά σε ένα οπτικό μέσο με μεγαλύτερο δείκτη διάθλασης, αρχίζει να διαχωρίζεται ανάλογα με το μήκος κύματος κάθε χρώματος. Στη συνέχεια θα παρακολουθήσουμε την πορεία του κόκκινου που κάμπτεται λιγότερο, και του μπλε που κάμπτεται περισσότερο. Βγαίνοντας από την απέναντι παράλληλη επιφάνεια, η διαδικασία αντιστρέφεται και το κάθε χρώμα κάμπτεται στην ίδια ακριβώς γωνία (ως προς την κάθετη στις παράλληλες επιφάνειες) με την οποία μπήκε στο υλικό.
Είναι λοιπόν προφανές, ότι οι διαχωρισμένες ακτίνες ταξιδεύουν πλέον παράλληλα και δεν ξαναενώνονται (το ίδιο φυσικά ισχύει και για τα άλλα ενδιάμεσα χρώματα). Πως ξαναγίνεται λοιπόν η ακτίνα λευκή;
Αν παρατηρήσουμε το σχέδιο στα δεξιά, θα δούμε ότι καθώς η λευκή ακτίνα αποτελείται στην πραγματικότητα από ένα μεγάλο σύνολο απειροελάχιστα λεπτών λευκών ακτίνων που υφίστανται την ίδια αλλαγή, όλα τα χρώματα συντίθεται για να δώσουν λευκό (θυμίζουμε, φαίνεται μαύρο στο σχέδιο), εκτός από τις τελείως «ακριανές» ακτίνες του κόκκινου και μπλε που όμως είναι τόσο λεπτές, που περνούν απαρατήρητες. Επίσης, απαρατήρητη περνά η ελαφρά «πάχυνση» της λευκής ακτίνας κατά την έξοδό της.
Μπαίνοντας το λευκό φως (μαύρο στο σχέδιο για πρακτικούς λόγους) λοξά σε ένα οπτικό μέσο με μεγαλύτερο δείκτη διάθλασης, αρχίζει να διαχωρίζεται ανάλογα με το μήκος κύματος κάθε χρώματος. Στη συνέχεια θα παρακολουθήσουμε την πορεία του κόκκινου που κάμπτεται λιγότερο, και του μπλε που κάμπτεται περισσότερο. Βγαίνοντας από την απέναντι παράλληλη επιφάνεια, η διαδικασία αντιστρέφεται και το κάθε χρώμα κάμπτεται στην ίδια ακριβώς γωνία (ως προς την κάθετη στις παράλληλες επιφάνειες) με την οποία μπήκε στο υλικό.
Είναι λοιπόν προφανές, ότι οι διαχωρισμένες ακτίνες ταξιδεύουν πλέον παράλληλα και δεν ξαναενώνονται (το ίδιο φυσικά ισχύει και για τα άλλα ενδιάμεσα χρώματα). Πως ξαναγίνεται λοιπόν η ακτίνα λευκή;
Αν παρατηρήσουμε το σχέδιο στα δεξιά, θα δούμε ότι καθώς η λευκή ακτίνα αποτελείται στην πραγματικότητα από ένα μεγάλο σύνολο απειροελάχιστα λεπτών λευκών ακτίνων που υφίστανται την ίδια αλλαγή, όλα τα χρώματα συντίθεται για να δώσουν λευκό (θυμίζουμε, φαίνεται μαύρο στο σχέδιο), εκτός από τις τελείως «ακριανές» ακτίνες του κόκκινου και μπλε που όμως είναι τόσο λεπτές, που περνούν απαρατήρητες. Επίσης, απαρατήρητη περνά η ελαφρά «πάχυνση» της λευκής ακτίνας κατά την έξοδό της.
Για παρόμοιο λόγο δεν βλέπουμε την ανάλυση του φάσματος αν κρατήσουμε ένα πρίσμα στον ήλιο, ή στον πυθμένα μίας πισίνας ακόμα και όταν ο ήλιος δεν είναι κάθετος. Για να φανούν τα χρώματα του φάσματος, η δέσμη του λευκού φωτός πρέπει να είναι (όπως στην εικόνα 1), πολύ λεπτή.
Ας δούμε τώρα ένα πιο δύσκολο θέμα. Γιατί συμβαίνει η διάθλαση; Και δεν εννοούμε τους νόμους της διάθλασης που είναι απλοί και υπάρχουν σε κάθε εγχειρίδιο Φυσικής, αλλά γιατί το φως συμπεριφέρεται έτσι.
Η πιο απλή εξήγηση είναι ότι το φως θέλει να είναι όσο πιο γρήγορο γίνεται, με την έννοια ότι θέλει να μειώσει τον χρόνο μετακίνησής του στο μηδέν. (Σύμφωνα με τη θεωρία της Σχετικότητας αυτό συμβαίνει πράγματι για το ίδιο το φως στο κενό, δεν ισχύει όμως για τον εξωτερικό παρατηρητή).
Ο Φερμά το είχε διατυπώσει κάπως διαφορετικά τον 17ο αι., ότι δηλαδή το φως επιλέγει τη χρονικά συντομότερη διαδρομή.
Όμως, μέσα από οπτικά μέσα όπως ο αέρας (πρακτικά χωρίς διαφορά από το κενό), το νερό, το γυαλί, το διαμάντι κλπ, η ταχύτητά του φωτός (σωστότερα, η ταχύτητα διάδοσής του) είναι σαφώς μικρότερη από αυτή στο κενό, γιατί απλά υπάρχουν «εμπόδια» με τη μορφή πεδίων των ατόμων. Στο νερό για παράδειγμα, η ταχύτητα του φωτός είναι το 75% της ταχύτητάς του στο κενό.
Ας δούμε τώρα ένα πιο δύσκολο θέμα. Γιατί συμβαίνει η διάθλαση; Και δεν εννοούμε τους νόμους της διάθλασης που είναι απλοί και υπάρχουν σε κάθε εγχειρίδιο Φυσικής, αλλά γιατί το φως συμπεριφέρεται έτσι.
Η πιο απλή εξήγηση είναι ότι το φως θέλει να είναι όσο πιο γρήγορο γίνεται, με την έννοια ότι θέλει να μειώσει τον χρόνο μετακίνησής του στο μηδέν. (Σύμφωνα με τη θεωρία της Σχετικότητας αυτό συμβαίνει πράγματι για το ίδιο το φως στο κενό, δεν ισχύει όμως για τον εξωτερικό παρατηρητή).
Ο Φερμά το είχε διατυπώσει κάπως διαφορετικά τον 17ο αι., ότι δηλαδή το φως επιλέγει τη χρονικά συντομότερη διαδρομή.
Όμως, μέσα από οπτικά μέσα όπως ο αέρας (πρακτικά χωρίς διαφορά από το κενό), το νερό, το γυαλί, το διαμάντι κλπ, η ταχύτητά του φωτός (σωστότερα, η ταχύτητα διάδοσής του) είναι σαφώς μικρότερη από αυτή στο κενό, γιατί απλά υπάρχουν «εμπόδια» με τη μορφή πεδίων των ατόμων. Στο νερό για παράδειγμα, η ταχύτητα του φωτός είναι το 75% της ταχύτητάς του στο κενό.
Εικόνα 4. Μία "απλοϊκή" προσπάθεια να εξηγηθεί η κάμψη του φωτός περνώντας λοξά σε πιο αργό περιβάλλον, είναι το καρότσι που επιβραδύνεται αρχικά «μονόπαντα» και υποχρεώνεται σε ελαφρά δεξιά στροφή, εξαιτίας του γεγονότος ότι οι δεξιοί του τροχοί βρίσκονται πρώτοι μέσα σε περιβάλλον αυξημένης αντίστασης.
Εικόνα 5.
Η καλύτερη εξήγηση δίνεται στην εικόνα 5, με το παράδειγμα ενός ανθρώπου που είναι στην ξηρά και βλέπει κάποιον να ζητάει βοήθεια, σε κάποια απόσταση μέσα στη θάλασσα. Από τις τρείς επιλογές διαδρομής που έχει, αυτή που θα τον φέρει συντομότερα κοντά στον άνθρωπο που χρειάζεται βοήθεια είναι να τρέξει τη μεγαλύτερη απόσταση στο έδαφος και στη συνέχεια να κινηθεί προς τον άνθρωπο κολυμπώντας, με μικρότερη φυσικά ταχύτητα (πράσινη διαδρομή). Οι άλλες δύο επιλογές διαδρομής είναι φανερό (και αποδεικνύεται μαθηματικά) ότι είναι πιο αργές. Αυτό ισχύει στην περίπτωση του παραδείγματος για οποιαδήποτε θέση του διασώστη και του κολυμβητή.
Η καλύτερη εξήγηση δίνεται στην εικόνα 5, με το παράδειγμα ενός ανθρώπου που είναι στην ξηρά και βλέπει κάποιον να ζητάει βοήθεια, σε κάποια απόσταση μέσα στη θάλασσα. Από τις τρείς επιλογές διαδρομής που έχει, αυτή που θα τον φέρει συντομότερα κοντά στον άνθρωπο που χρειάζεται βοήθεια είναι να τρέξει τη μεγαλύτερη απόσταση στο έδαφος και στη συνέχεια να κινηθεί προς τον άνθρωπο κολυμπώντας, με μικρότερη φυσικά ταχύτητα (πράσινη διαδρομή). Οι άλλες δύο επιλογές διαδρομής είναι φανερό (και αποδεικνύεται μαθηματικά) ότι είναι πιο αργές. Αυτό ισχύει στην περίπτωση του παραδείγματος για οποιαδήποτε θέση του διασώστη και του κολυμβητή.
Παρόμοια, και η ακτίνα του φωτός, καθώς δεν ξέρει παρά τη γωνία με την οποία συναντά την επιφάνεια διαχωρισμού, η μόνη δυνατότητα που έχει είναι να υπακούει στον σχετικό μαθηματικό νόμο (του Snell) που λέει ότι ο λόγος των ημιτόνων των γωνιών που σχηματίζει η ακτίνα με την κάθετη στην επιφάνεια διαχωρισμού είναι ίσος με τον λόγο των ταχυτήτων στα δύο μέσα. Έτσι, σε όποιο σημείο του πυκνότερου διαθλαστικά μέσου και να καταλήξει η ακτίνα, θα είναι στον μικρότερο χρόνο. Τελικά, ο καλύτερος συμβιβασμός πετυχαίνει αυτό που πραγματικά επιδιώκει το φως, να καμφθεί δηλαδή η ακτίνα «τόσο όσο» ώστε η συνολική καθυστέρηση να είναι η ελάχιστη.
ΥΓ1. Με αντίστοιχο τρόπο, ένα πολύ ισχυρό βαρυτικό πεδίο (από ένα μεγάλο ουράνιο σώμα πχ) παραμορφώνει τον χώρο στην περιοχή του και δρα επιβραδυντικά για το φως (καθυστερώντας τη ροή του χρόνου), οπότε η πορεία του φωτός "κάμπτεται" (εικόνα κάτω).
Μια άλλη περίπτωση βαθμιαίας "κάμψης" του φωτός, είναι η χρήση γυαλιού μεταβαλλόμενου δείκτη διάθλασης (εικόνα επάνω). Το φως κάμπτεται προς την πλευρά που ο δείκτης διάθλασης αυξάνεται. Κάτι που γίνεται και στην ατμόσφαιρα, εξαιτίας της μεταβαλλόμενης πυκνότητά της.
ΥΓ2. Σε συνθήκες εργαστηρίου, σε πολύ υψηλό κενό και σε απόλυτο μηδέν θερμοκρασίας, χρησιμοποιώντας άτομα νατρίου και laser, επιστήμονες πέτυχαν να επιβραδύνουν το φως στην ταχύτητα των 60km/h, μικρότερη δηλαδή και απ' αυτήν ενός αυτοκινήτου!
104. Μετασχηματιστές και κιβώτια ταχυτήτων.
Τι σχέση έχουν οι μετασχηματιστές με τα κιβώτια ταχυτήτων*; Πολλή, καθώς και οι δύο συσκευές λειτουργούν με παρόμοιες αρχές Φυσικής, και μάλιστα είναι πιο εύκολο να καταλάβουμε τη λειτουργία ενός μετασχηματιστή, αν την συγκρίνουμε με αυτήν ενός κιβωτίου ταχυτήτων.
Στο τελευταίο, όση ισχύς μπαίνει, τόση και βγαίνει, αν εξαιρέσουμε τις μικρές εσωτερικές θερμικές απώλειες. Το ίδιο ισχύει και για τον μετασχηματιστή.
Στο κιβώτιο ταχυτήτων η ισχύς εκφράζεται σαν: Ρ = Μ x Rpm, αντίστοιχα για τον (μονοφασικό) μετασχηματιστή ισχύει: P = V x I. Οπότε όταν ο ένα όρος αυξάνεται, εφόσον η συνολική ισχύς παραμένει (σχεδόν) σταθερή, ο άλλος μειώνεται κατά το ίδιο ποσοστό.
Θα μπορούσαμε μάλιστα να παρομοιάζουμε την ροπή (Μ) στο κιβώτιο ταχυτήτων με την ένταση (Ι) στον μετασχηματιστή, και αντίστοιχα τις στροφές (Rpm) στο κιβώτιο ταχυτήτων με την τάση (V) στον μετασχηματιστή.
Η πλευρά του κιβωτίου ταχυτήτων που μεταφέρει τη μεγαλύτερη ροπή έχει το μεγαλύτερο σε διάμετρο γρανάζι αλλά και τον χοντρότερο άξονα, αντίστοιχα η πλευρά του μετασχηματιστή με τη μεγαλύτερη ένταση έχει τον χοντρότερο αγωγό και καλώδια (αλλά τις λιγότερες σπείρες, και εδώ τα πράγματα είναι αντίστροφα με το κιβώτιο ταχυτήτων, καθώς το γρανάζι μεγάλης ροπής έχει και τα περισσότερα δόντια).
Και στις δύο περιπτώσεις, μπορούμε να έχουμε είτε μία, ή περισσότερες σχέσεις μετάδοσης. Και στις δύο περιπτώσεις, η ροή ισχύος μπορεί να γίνει το ίδιο καλά και προς τις δύο κατευθύνσεις (οπότε στην εικόνα του μετασχηματιστή επάνω, η επισήμανση primary και secondary έχουν μόνο συμβατική αξία). Και στις δύο περιπτώσεις, ο συνολικός όγκος της συσκευής είναι (προφανώς) ενδεικτικός της δυναμικότητας σε μέγιστη μεταφερόμενη ισχύ.
Τόσο τα κιβώτια ταχυτήτων όσο και οι μετασχηματιστές δεν απορροφούν ισχύ από την τροφοδοσία τους εφόσον δεν μεταφέρουν ισχύ στην έξοδό τους, παρά μόνο την ελάχιστη που απαιτείται για την αντιμετώπιση των θερμικών απωλειών τους. Και όσο φορτίζεται η έξοδός τους, τόσο (και αυτόματα) αυξάνεται και η απορροφούμενη ισχύς.
Αντίστοιχο είναι και ένα άλλο φαινόμενο, αυτό της απότομης αύξησης της απαιτούμενης ροπής (στο κιβώτιο ταχυτήτων) και της έντασης (στον μετασχηματιστή), εφόσον τους τροφοδοτήσουμε ξαφνικά. Αυτό είναι πιο εύκολο να ελεγχθεί στα κιβώτια ταχυτήτων καθώς συνήθως τροφοδοτούνται μέσω συμπλέκτη που επιτρέπει κάποια αρχική ολίσθηση. Αντίθετα, στους μετασχηματιστές η εφαρμογή της τάσης τυπικά γίνεται απότομα, με το κλείσιμο** ενός διακόπτη. Αλλά ακόμα και σ’ αυτή στην περίπτωση, η «εμπλοκή» στο ηλεκτρικό δίκτυο μπορεί να γίνει ομαλότερα με τη χρήση συστήματος χειροκίνητης ή και αυτόματης σταδιακής αύξησης της τάσης, μια τεχνική που εφαρμόζεται συνήθως σε πολύ μεγάλες συσκευές.
Το φαινόμενο που αναφέρθηκε παραπάνω, στην περίπτωση του κιβωτίου ταχυτήτων οφείλεται στη μηχανική αδράνεια των στρεφόμενων μερών (γραναζιών και αξόνων), ενώ στον μετασχηματιστή στην «αδράνεια» του μαγνητικού κυκλώματος του πυρήνα του, που πρέπει να μαγνητιστεί ξαφνικά.
* Ένα απλό κιβώτιο ταχυτήτων με μία μόνο σχέση μετάδοσης (όπως στην εικόνα) ονομάζεται γενικά και μειωτήρας, παρόλο που μπορεί να χρησιμοποιηθεί και για την αύξηση της ταχύτητας περιστροφής.
Τόσο τα κιβώτια ταχυτήτων όσο και οι μετασχηματιστές δεν απορροφούν ισχύ από την τροφοδοσία τους εφόσον δεν μεταφέρουν ισχύ στην έξοδό τους, παρά μόνο την ελάχιστη που απαιτείται για την αντιμετώπιση των θερμικών απωλειών τους. Και όσο φορτίζεται η έξοδός τους, τόσο (και αυτόματα) αυξάνεται και η απορροφούμενη ισχύς.
Αντίστοιχο είναι και ένα άλλο φαινόμενο, αυτό της απότομης αύξησης της απαιτούμενης ροπής (στο κιβώτιο ταχυτήτων) και της έντασης (στον μετασχηματιστή), εφόσον τους τροφοδοτήσουμε ξαφνικά. Αυτό είναι πιο εύκολο να ελεγχθεί στα κιβώτια ταχυτήτων καθώς συνήθως τροφοδοτούνται μέσω συμπλέκτη που επιτρέπει κάποια αρχική ολίσθηση. Αντίθετα, στους μετασχηματιστές η εφαρμογή της τάσης τυπικά γίνεται απότομα, με το κλείσιμο** ενός διακόπτη. Αλλά ακόμα και σ’ αυτή στην περίπτωση, η «εμπλοκή» στο ηλεκτρικό δίκτυο μπορεί να γίνει ομαλότερα με τη χρήση συστήματος χειροκίνητης ή και αυτόματης σταδιακής αύξησης της τάσης, μια τεχνική που εφαρμόζεται συνήθως σε πολύ μεγάλες συσκευές.
Το φαινόμενο που αναφέρθηκε παραπάνω, στην περίπτωση του κιβωτίου ταχυτήτων οφείλεται στη μηχανική αδράνεια των στρεφόμενων μερών (γραναζιών και αξόνων), ενώ στον μετασχηματιστή στην «αδράνεια» του μαγνητικού κυκλώματος του πυρήνα του, που πρέπει να μαγνητιστεί ξαφνικά.
* Ένα απλό κιβώτιο ταχυτήτων με μία μόνο σχέση μετάδοσης (όπως στην εικόνα) ονομάζεται γενικά και μειωτήρας, παρόλο που μπορεί να χρησιμοποιηθεί και για την αύξηση της ταχύτητας περιστροφής.
**Κλείσιμο με την έννοια του κλεισίματος των επαφών του, ή αλλιώς ενεργοποίησή του.
Περιέργως, δεν βρίσκουμε μια εύκολη απάντηση στο ερώτημα αυτό, για τα σύγχρονα αεροπλάνα.
Σ’ έναν κινητήρα αντίδρασης όμως (jet* ή πυραυλοκινητήρα), η ισχύς δεν προκύπτει από τη στρέψη ενός άξονα, αλλά από την επιτάχυνση μάζας αερίων προς τα έξω. Στην περίπτωση αυτή, η ισχύς υπολογίζεται από τον τύπο:
P = F x V, όπου P: ισχύς, F: ώση, V: ταχύτητα κινητήρα, δηλαδή ταχύτητα αεροσκάφους/πυραύλου.
Το μέγεθος που μετριέται άμεσα είναι η ώση (παλιότερα με ελατήρια, τώρα πιεζοηλεκτρικά) οπότε η ισχύς προκύπτει από τον υπολογισμό που εμπεριέχει την ταχύτητα του συστήματος (η οποία βέβαια μπορεί να μεταβάλλεται).
Θα έχετε ενδεχομένως παρατηρήσει, ότι ειδικά σε αρκετά παλιά μηχανήματα, οι μασίφ ακτίνες των (μεγάλων) τροχών ή τροχαλιών ήταν συνήθως καμπυλωτές, παρά ίσιες.
107. Ηλεκτρολυτική διάβρωση, μια ανεπιθύμητη μπαταρία.
Η ηλεκτρολυτική (ή ηλεκτροχημική) διάβρωση είναι ένα φυσικό φαινόμενο που συμβαίνει όταν δύο διαφορετικά μέταλλα βρίσκονται σε αγώγιμη επαφή, και ταυτόχρονα σε ηλεκτρολυτικό περιβάλλον.
Ενώ στα παλαιότερα αεροπλάνα που χρησιμοποιούσαν εμβολοφόρους κινητήρες με έλικες, η ισχύς σε ίππους αναφέρονταν σαφώς (αυτό εξακολουθεί ακόμα να ισχύει για κάθε ελικοφόρο αεροπλάνο), στα σύγχρονα αεροπλάνα με κινητήρες jet ή στους πυραύλους, αναφέρεται συνήθως μόνον η ώθηση που προσφέρει ο κινητήρας (ή οι κινητήρες).
Σ’ έναν εμβολοφόρο κινητήρα, που πρακτικά όλη την (ωφέλιμη) ισχύ του την παρέχει στην έλικα, η μέτρηση γίνεται σε ίππους (ή πιο πρόσφατα σε kW), όπως και σε έναν κινητήρα αυτοκινήτου, σύμφωνα με τον τύπο:
P = T x Rpm, όπου P: ισχύς, T: ροπή, Rpm: στροφές.
Έτσι τα μετρούμενα μεγέθη είναι η ροπή (με κάποιο είδους φρένο ή γεννήτρια) και οι στροφές, ενώ η ισχύς προκύπτει υπολογιστικά.
Σ’ έναν εμβολοφόρο κινητήρα, που πρακτικά όλη την (ωφέλιμη) ισχύ του την παρέχει στην έλικα, η μέτρηση γίνεται σε ίππους (ή πιο πρόσφατα σε kW), όπως και σε έναν κινητήρα αυτοκινήτου, σύμφωνα με τον τύπο:
P = T x Rpm, όπου P: ισχύς, T: ροπή, Rpm: στροφές.
Έτσι τα μετρούμενα μεγέθη είναι η ροπή (με κάποιο είδους φρένο ή γεννήτρια) και οι στροφές, ενώ η ισχύς προκύπτει υπολογιστικά.
Σ’ έναν κινητήρα αντίδρασης όμως (jet* ή πυραυλοκινητήρα), η ισχύς δεν προκύπτει από τη στρέψη ενός άξονα, αλλά από την επιτάχυνση μάζας αερίων προς τα έξω. Στην περίπτωση αυτή, η ισχύς υπολογίζεται από τον τύπο:
P = F x V, όπου P: ισχύς, F: ώση, V: ταχύτητα κινητήρα, δηλαδή ταχύτητα αεροσκάφους/πυραύλου.
Το μέγεθος που μετριέται άμεσα είναι η ώση (παλιότερα με ελατήρια, τώρα πιεζοηλεκτρικά) οπότε η ισχύς προκύπτει από τον υπολογισμό που εμπεριέχει την ταχύτητα του συστήματος (η οποία βέβαια μπορεί να μεταβάλλεται).
Έτσι προκύπτει το φαινομενικά παράδοξο, ένα jet αεροπλάνο με τους κινητήρες του σε πλήρη ισχύ αλλά φρεναρισμένο και ακίνητο στο έδαφος, να έχει μηδενική (ωφέλιμη) ισχύ, παρά τις τεράστιες ποσότητες καυσίμου που προφανώς καταναλίσκει.
Στο λογικό ερώτημα, πού πηγαίνει όλη αυτή η ισχύς όσο το αεροπλάνο δεν κινείται, η απάντηση είναι σε θέρμανση και διαταραχή (στροβιλισμό) του αέρα, που βέβαια τελικά καταλήγει και αυτή σε θέρμανση του αέρα.
Για σύγκριση, αν θέλουμε να εξομοιώσουμε την ισχύ ενός ακίνητου αεροσκάφους jet με έναν εμβολοφόρο κινητήρα, είναι σαν ένα (πισωκίνητο) αυτοκίνητο να κάνει burn out με τους εμπρός τροχούς φρεναρισμένους, οπότε όλη η ισχύς του κινητήρα αναλώνεται στο να καίει από την τριβή τα πίσω λάστιχά του!
Στο λογικό ερώτημα, πού πηγαίνει όλη αυτή η ισχύς όσο το αεροπλάνο δεν κινείται, η απάντηση είναι σε θέρμανση και διαταραχή (στροβιλισμό) του αέρα, που βέβαια τελικά καταλήγει και αυτή σε θέρμανση του αέρα.
Για σύγκριση, αν θέλουμε να εξομοιώσουμε την ισχύ ενός ακίνητου αεροσκάφους jet με έναν εμβολοφόρο κινητήρα, είναι σαν ένα (πισωκίνητο) αυτοκίνητο να κάνει burn out με τους εμπρός τροχούς φρεναρισμένους, οπότε όλη η ισχύς του κινητήρα αναλώνεται στο να καίει από την τριβή τα πίσω λάστιχά του!
*αν όμως πρόκειται για κινητήρα jet που δίνει όλη του την ισχύ σε άξονα που κινεί έλικα (turboprop), τότε ο υπολογισμός γίνεται με την πρώτη μέθοδο. Το ίδιο ισχύει και για τους ατμοστροβίλους.
ΥΓ. Μία ιδιαίτερη περίπτωση είναι οι ατμομηχανές των παλαιών τρένων, που συνήθως συγκρίνονταν με τη ροπή τους, οπότε παραδοσιακά οι μονάδες που χρησιμοποιούνται ήταν πόδια επί λίβρες* (feet x pounds). Και αυτό επειδή οι ατμομηχανές αναπτύσσουν τη μέγιστη ροπή τους λίγο πριν ξεκινήσουν (οπότε η ισχύς τους, σύμφωνα με αυτά που προαναφέρθηκαν, είναι ακόμα μηδέν), αλλά είναι αυτή η ροπή που είναι ενδεικτική του φορτίου που μπορούν να σύρουν. Η μεγάλη ροπή των ατμομηχανών και ο μικρός σχετικά συντελεστής τριβής των τροχών με τις ράγες, προκαλούσε εντυπωσιακό "πατινάρισμα" των τροχών σε βαρυφορτωμένα τρένα ή "βιαστικούς" μηχανοδηγούς (εικόνα κάτω).
* Λίβρες και πάουντς είναι ουσιαστικά το ίδιο πράγμα. Η μονάδα είναι το Pound, αλλά το σύμβολο η Lb.
106. Οι καμπύλες ακτίνες τροχών και τροχαλιών.
Αυτό μοιάζει σαν περιττή πολυπλοκότητα (και σπατάλη μετάλλου), ειδικά σε μια εποχή που η κατασκευή των καλουπιών για τη χύτευση μεταλλικών αντικειμένων γίνονταν με το χέρι.
Η εξήγηση έχει να κάνει ακριβώς με το γεγονός ότι οι μεγάλες μεταλλικές τροχαλίες ή τροχοί κατασκευάζονταν με χύτευση, η οποία όμως ακόμα δεν είχε εξελιχθεί αρκετά, ώστε να αποφεύγονται ρωγμές κατά τη συστολή του εξαρτήματος με την ψύξη του.
Οι καμπύλες ακτίνες παρείχαν κάποιο βαθμό ελαστικότητας, που επέτρεπε ώστε οι εσωτερικές τάσεις που αναπτύσσονταν κατά την ψύξη του μετάλλου, να μην καταλήγουν σε ρηγμάτωση.
Επιπλέον, στην περίπτωση των τροχών (σιδηροδρομικών πχ), το καμπύλο σχήμα λειτουργούσε στοιχειωδώς και σαν "ελατήριο" μειώνοντας τους κραδασμούς και τις καταπονήσεις. Και τελικά, μάλλον τους έκανε και ομορφότερους.
Η ηλεκτρολυτική (ή ηλεκτροχημική) διάβρωση είναι ένα φυσικό φαινόμενο που συμβαίνει όταν δύο διαφορετικά μέταλλα βρίσκονται σε αγώγιμη επαφή, και ταυτόχρονα σε ηλεκτρολυτικό περιβάλλον.
Στην περίπτωση αυτή δημιουργείται μια μπαταρία και μάλιστα «βραχυκυκλωμένη», καθώς θετικά ιόντα διαφεύγουν από την επιφάνεια του λιγότερου «ευγενούς» μετάλλου, ενώ ταυτόχρονα ηλεκτρόνιά του κινούνται μέσω της αγώγιμης επαφής, προς το πιο ευγενές μέταλλο.
Αλλά ενώ η μετακίνηση ηλεκτρονίων δεν είναι πρόβλημα, τα θετικά ιόντα ΕΙΝΑΙ υλικό, και σημαίνει τη σταδιακή διάλυσή του.
Με αυτόν το τρόπο, το λιγότερο ευγενές μέταλλο θα φθαρεί τελικά μέχρις της εξαφάνισής του.
Εικόνα 1. Η πιο συνηθισμένη περίπτωση ηλεκτρολυτικής διάβρωσης είναι η επαφή σιδήρου με χαλκό, σε θαλασσινό περιβάλλον ή μέσα στο έδαφος.
Εικόνα 2. Πώς τα διαφορετικά μέταλλα λειτουργούν σαν μπαταρία, εφόσον υπάρχει αγώγιμη επαφή μεταξύ τους. Η άνοδος της μπαταρίας, η οποία παρέχει τα θετικά ιόντα, φθείρεται.
Ένα χαρακτηριστικό και μάλιστα έντονο ηλεκτρολυτικό περιβάλλον, είναι το θαλασσινό νερό αλλά και το έδαφος, αν και το δεύτερο λιγότερο έντονο και μεγαλύτερης ηλεκτρικής αντίστασης, κάτι που καθορίζει και τον τρόπο αντιμετώπισης του προβλήματος.
Επιπλέον, μεταλλικοί σωλήνες στο έδαφος που μεταφέρουν υγρά καύσιμα, υποφέρουν και από τη διάβρωση που δημιουργεί (έμμεσα) ο στατικός ηλεκτρισμός που αναπτύσσουν οι υδρογονάνθρακες κατά τη ροή τους, εξαιτίας της τριβής τους με τα τοιχώματα.
Τέλος, ακόμα και απλές σιδερένιες ράβδοι μέσα στο έδαφος μπορούν να διαβρωθούν ηλεκτρολυτικά, εφόσον κυκλοφορεί ηλεκτρικό ρεύμα μέσα από αυτές χωρίς να γίνεται αντιληπτό (πχ από επαγωγική τάση, όταν βρίσκονται κοντά σε γραμμές υψηλής τάσης, υποσταθμούς κλπ).
Εικόνα 3. Κάθε μέταλλο του πίνακα, προστατεύεται από οποιοδήποτε άλλο μέταλλο βρίσκεται χαμηλότερά του στη σειρά, εφόσον βρίσκονται σε επαφή. Τα πιο συνηθισμένα μέταλλα που χρησιμοποιούνται για προστασία και προφανώς βρίσκονται στον «πάτο» του πίνακα, είναι ο Ψευδάργυρος (Zinc) και το Μαγνήσιο (Magnesium). Προσέξτε την απόσταση του Τιτανίου από το Αλουμίνιο. Αυτή η απόσταση έχει δημιουργήσει προβλήματα σε αεροπορικές κατασκευές από Αλουμίνιο που χρησιμοποιούν βίδες από Τιτάνιο σε θαλασσινό περιβάλλον, οπότε στις περιπτώσεις αυτές συνήθως οι βίδες Τιτανίου αντικαθίστανται από ανοξείδωτες.
Ο καλύτερος και απλούστερος τρόπος αντιμετώπισης, όταν υπάρχουν οι συνθήκες που μπορούν να προκαλέσουν ηλεκτρολυτική διάβρωση, είναι η ηλεκτρική απομόνωση των δύο διαφορετικών μεταλλικών υλικών έτσι ώστε να μην έχουν αγώγιμη επαφή μεταξύ τους, παρεμβάλλοντας ακόμα και ένα πολύ μικρό κομμάτι λάστιχου, πλαστικού ή ξύλου, καθώς η διαφορά δυναμικού (τάση) που αναπτύσσεται είναι ελάχιστη.
Θα πρέπει να δοθεί όμως προσοχή, ώστε και οποιαδήποτε συνδετικά στοιχεία μεταξύ των μεταλλικών υλικών που μονώθηκαν, πχ μπουλόνια κλπ, να είναι επίσης κατάλληλα μονωμένα, ώστε να μην «βραχυκυκλώνουν» τη βασική μόνωση.
Η πιο συνηθισμένη μέθοδος προστασίας όμως, είναι η παθητική και η ενεργητική καθοδική προστασία (ονομάζονται έτσι επειδή προστατεύεται η κάθοδος), που επεξηγούνται στο παρακάτω σχήμα.
Εικόνα 4. Οι δύο συνηθισμένες μέθοδοι προστασίας, όταν δεν μπορεί να χρησιμοποιηθεί η απομόνωση των διαφορετικών μετάλλων: Αριστερά η «παθητική» μέθοδος της θυσιαζόμενης ανόδου, συνήθως ηλεκτρόδιο ψευδαργύρου ή μαγνησίου, και δεξιά η «ενεργητική» μέθοδος με την επιβολή ηλεκτρικού ρεύματος συνεχούς τάσης, ώστε το προστατευόμενο υλικό να γίνει λίγο πιο αρνητικό από το ηλεκτρόδιο. Η πρώτη μέθοδος χρησιμοποιείται συνήθως στα καράβια, ενώ η δεύτερη στους σωλήνες. Η δεύτερη μέθοδος συνδυάζεται συχνά και με κάποιου είδους μονωτικής επικάλυψης της επιφάνειας.
Εικόνα 5. Η εφαρμογή των θυσιαζόμενων ανοδίων σε σκάφος (τα λευκά διάσπαρτα πλακίδια). Στα σκάφη, το πρόβλημα είναι επικεντρωμένο στην περιοχή της πρύμνης, όπου βρίσκεται η συνήθως μπρούτζινη έλικα και τα επίσης μπρούτζινα έδρανα της ίδιας αλλά και του τιμονιού. Εξαιτίας λοιπόν της επαφής με τον μπρούτζο που αποτελείται κυρίως από χαλκό, το σίδερο της περιοχής της πρύμνης θα διαβρώνονταν. Τα ανόδια συνήθως αλλάζονται κατά τον δεξαμενισμό του σκάφους, για τις συνηθισμένες εργασίες καθαρισμού, βαφής κλπ.
Μία επίσης συνηθισμένη μέθοδος προστασίας είναι η εν θερμώ επιψευδαργύρωση του σιδήρου, που χρησιμοποιείται στις δομικές σιδηροκατασκευές και στην αυτοκινητοβιομηχανία (στην τελευταία τουλάχιστον για το κάτω μέρος του αμαξώματος), για την αυξημένη προστασία που απαιτείται από το αλάτι που ρίχνεται τον χειμώνα στους δρόμους.
Η επιψευδαργύρωση έχει μάλιστα το διπλό όφελος να προστατεύει τον σίδηρο και από την ατμοσφαιρική διάβρωση, που εφόσον δεν υπάρχει επαφή με διαφορετικό μέταλλο είναι η πρωταρχική αιτία διάβρωσης.
Για το τέλος, αφήσαμε την ενδιαφέρουσα ιστορία για το πώς ξεκίνησε η καθοδική προστασία, και μάλιστα με επιτυχία.... που προκάλεσε την αποτυχία της!
Το έτος ήταν το 1824, και το πρόβλημα προς αντιμετώπιση ήταν η διάβρωση της χάλκινης επικάλυψης της γάστρας του HMS Samarang, για την οποία χρησιμοποιήθηκαν θυσιαζόμενα ανόδια από σίδηρο.
Η ιδέα ήταν σωστή από ηλεκτροχημικής πλευράς και δούλεψε, αλλά με μία απροσδόκητη παρενέργεια.
Οι μικροοργανισμοί που προηγουμένως δηλητηριάζονταν από τα ιόντα χαλκού που διαλύονταν στην θάλασσα, τώρα έκαναν «πάρτι» στα χάλκινα ύφαλα του σκάφους, μειώνοντας σημαντικά την ταχύτητά του!
Οπότε το Ναυαρχείο αποφάσισε ότι το μικρότερο κακό ήταν η διάβρωση του χαλκού, και τα σιδερένια ανόδια καταργήθηκαν!
108. Θερμοκρασία και άνεση.
Όταν αναφερόμαστε στη άνεση που μας εξασφαλίζει ένα περιβάλλον, συνήθως σχολιάζουμε τη θερμοκρασία του.
Η θερμοκρασία όμως είναι μόνο η μία πλευρά του νομίσματος, καθώς η άνεση που νιώθουμε σε δεδομένο περιβάλλον εξαρτάται και από την υγρασία του αέρα για τις ψηλότερες θερμοκρασίες, ενώ για τις χαμηλότερες εξαρτάται κυρίως από την ταχύτητα του ανέμου.
Ο βασικός λόγος που συμβαίνει αυτό είναι η εφίδρωση του ανθρώπινου σώματος, η οποία λειτουργεί «ψυκτικά» για το δέρμα και κατά συνέπεια και για το ανθρώπινο σώμα.
Επίσης, σημαντική υγρασία παράγει το ίδιο το σώμα καθώς οξειδώνει τις τροφές (βασικά υδατάνθρακες), και η οποία απομακρύνεται με την εκπνοή.
Αυτό είναι αντίστοιχο με την καύση των υδρογονανθράκων στους κινητήρες των αυτοκινήτων, όπου την υγρασία την βλέπουμε σαν συννεφάκι τα κρύα πρωϊνά, όπως εξάλλου και την αναπνοή μας.
Εικόνα 1. Πώς συμπυκνώνεται η υγρασία του αέρα σε σύννεφο. Το Dewpoint (σημείο δρόσου) είναι ένας όρος που χρησιμοποιείται πολύ στη μετεωρολογία, και είναι η θερμοκρασία που για δεδομένο ποσοστό υγρασίας στον αέρα θα επέλθει η συμπύκνωσή της. Στην εικόνα, καθώς ο αέρας ανεβαίνει ψύχεται (τυπικά κατά 1 βαθμό Κελσίου ανά 100 μέτρα) και αφού το σημείο δρόσου του είναι 60 F (οι μονάδες θερμοκρασίας εδώ δεν έχουν σημασία), όταν φθάσει σε ύψος που η θερμοκρασία του αέρα θα είναι 60 F, θα ξεκινήσει η υγροποίησή του. Οι συμπυκνωμένοι υδρατμοί όμως εξακολουθούν και ανεβαίνουν για κάποιο διάστημα, εξαιτίας της λανθάνουσας θερμότητας που εκλύεται κατά τη φάση της υγροποίησής τους (0.5 kcal/g νερού), γι' αυτό και τα σύννεφα δεν έχουν λεπτό και επίπεδο σχήμα.
Εδώ θα πρέπει να θυμίσουμε ότι ο αέρας περιέχει πάντα μια ποσότητα νερού σε αέρια μορφή, και αυτή την ποσότητα τη λέμε υγρασία.
Η υγρασία αυτή όσο παραμένει σε «διάλυση» είναι αόρατη, ενώ γίνεται ορατή όταν ο αέρας γίνει κορεσμένος, όταν δηλαδή ο αέρας φθάσει στη μέγιστη ποσότητα νερού που μπορεί να συγκρατήσει σε διάλυση και τότε εμφανίζονται οι γνωστές σταγόνες συμπύκνωσης της υγρασίας.
Χαρακτηριστικό παράδειγμα είναι το νερό που συμπυκνώνεται και τρέχει από τις μονάδες ψύξης των κλιματιστικών*, και βέβαια τα σύννεφα, όπου η υγρασία της ατμόσφαιρας συμπυκνώνεται όταν ο αέρας καθώς ανεβαίνει έχει ψυχθεί αρκετά ώστε το διάλυμα του νερού στον αέρα να γίνει κορεσμένο.
Γι’ αυτό, μας ενδιαφέρει περισσότερο η σχετική υγρασία του αέρα, δηλαδή πόσο νερό βρίσκεται διαλυμένο στον αέρα σε σχέση με τη μέγιστη ποσότητα που μπορεί να διαλυθεί (πάντα για τις δεδομένες συνθήκες θερμοκρασίας κυρίως, και πίεσης δευτερευόντως), παρά η απόλυτη ποσότητα του νερού που περιέχεται στον αέρα.
Και αυτό, επειδή το ποσοστό υγρασίας μας δείχνει πόσο κοντά βρισκόμαστε στο να αρχίσει η υγρασία να συμπυκνώνεται (κάτι που θα συμβεί όταν η θερμοκρασία του αέρα πέσει λίγο ακόμα), δημιουργώντας ομίχλη ή υγραίνοντας τις επιφάνειες, κάτι που ενδιαφέρει από τους μετεωρολόγους μέχρι ... τους βαφείς.
*Αν θέλουμε να κάνουμε μόνο αφύγρανση του αέρα, αρκεί μετά την ψύξη του και την αφαίρεση μέρους του νερού που περιέχει, να τον ξαναθερμάνουμε.
Εικόνα 2. Ποσότητα νερού που κρατάει διαλυμένη και σε αιώρηση ο αέρας, ανάλογα με τη θερμοκρασία και το ποσοστό της σχετικής υγρασίας. Η μέγιστη ποσότητα νερού που μπορεί να κρατήσει σε διάλυση ο αέρας εκφράζεται με τη μπλέ γραμμή του 100%. Δηλαδή στους 25 C ένα κυβικό μέτρο αέρα μπορεί να κρατήσει σε διάλυση μέχρι 23 γραμμάρια νερού.
Εικόνα 3. Παραστατική απεικόνιση μιας ποσότητας αέρα κεκορεσμένου σε υγρασία (αριστερά) που καθώς βαθμιαία τον ψύχουμε η υγρασία του συμπυκνώνεται σε νερό. Θα παρατηρήσετε ότι η συνολική ποσότητα νερού (σε αέρια και υγρή μορφή) παραμένει περίπου σταθερή.
Οι θερμοκρασίες αντιστοιχούν από αριστερά σε 35, 25, 10 και 0 βαθμούς Κελσίου.
Και μια μικρή άσκηση: Πόσος είναι ο όγκος του δοχείου?
Απάντηση: Από τον πίνακα της εικόνας 1 βλέπουμε ότι στους 95 F, δηλαδή στους 35 C, ο κεκορεσμένος αέρας συγκρατεί 40 g νερό ανά 1000 l αέρα. Άρα, για να έχουμε 1.9 g νερού στον κεκορεσμένο αέρα, θα πρέπει να έχουμε (1.9/40) Χ 1000 = 47.5 l αέρα, συνεπώς και δοχείου.
Μετά από τα παραπάνω εισαγωγικά, ας δούμε πώς μας επηρεάζει η θερμοκρασία του αέρα.
Όπως είπαμε, το σώμα μας αποβάλλει υγρασία με την αναπνοή, και παράγει ιδρώτα για να ρυθμίσει τη θερμοκρασία του με την ψύξη που προκαλεί η εξάτμισή του.
Επιπλέον, σε συνθήκες αυξημένης θερμοκρασίας διαστέλλονται τα επιφανειακά αιμοφόρα αγγεία, ώστε το αίμα να μπορέσει να ψυχθεί καλύτερα μέσα από το δέρμα, που όπως είπαμε ψύχεται με την εξάτμιση του ιδρώτα.
Έτσι, δεν είναι περίεργο που όσο πιο ξηρός είναι ο αέρας, δηλαδή όσο λιγότερη υγρασία περιέχει, τόσο πιο εύκολα εξατμίζεται ο ιδρώτας και τόσο πιο αποτελεσματική είναι η ψύξη του δέρματος, άρα και του σώματος.
Για τον λόγο αυτό υπάρχουν πίνακες που συνδυάζουν τη θερμοκρασία με την υγρασία, και δείχνουν ποιοι συνδυασμοί είναι πιο αποτελεσματικοί (comfort zone) για να νοιώθει ο άνθρωπος άνετα με το περιβάλλον του, και ποιοι είναι δυσμενέστεροι.
Και συμβαίνει, σε περιοχές ερήμου με υψηλή θερμοκρασία περιβάλλοντος αλλά με πολύ χαμηλή υγρασία, η αίσθηση να μην είναι δυσάρεστη καθώς ο ιδρώτας εξατμίζεται αμέσως.
Εικόνα 4. Ζώνες μεγαλύτερης ή μικρότερης θερμικής καταπόνησης, σε σχέση με τον συνδυασμό θερμοκρασίας / σχετικής υγρασίας. Κάτω αριστερά με μωβ χρώμα, η ζώνη άνεσης, ενώ τα βέλη δείχνουν ποιος συνδυασμός ισχύει σε τρείς τυπικές περιοχές της Β. Αμερικής.
Εικόνα 5. Ένας πίνακας που δείχνει τον ιδανικό συνδυασμό θερμοκρασίας και υγρασίας για την ευεξία και υγεία του ανθρώπου (μπλε περιοχή). Χαμηλότερη υγρασία (μωβ), δημιουργεί δερματικούς και αναπνευστικούς ερεθισμούς καθώς και έντονα προβλήματα από στατικά ηλεκτρικά φορτία, ενώ υψηλότερη υγρασία ευνοεί την ανάπτυξη ακάρεων (mites) και μούχλας (mould) στο περιβάλλον.
Από την άλλη πλευρά, όταν ο αέρας είναι ψυχρός, η επίδρασή του ανέμου δημιουργεί αίσθηση εντονότερου ψύχους, καθώς ο άνεμος απομακρύνει γρήγορα το ακίνητο στρώμα αέρα που σχηματίζεται γύρω από το σώμα μας και έχει θερμανθεί κάπως απ’ αυτό.
Αυτό είναι εύκολο να το καταλάβουμε καθώς ξέρουμε ότι τα ψυγεία των αυτοκινήτων για παράδειγμα που πρέπει να αποβάλουν τη θερμότητα του κινητήρα, είναι τόσο πιο αποτελεσματικά, όσο πιο γρήγορα κινείται το αυτοκίνητο.
Ο άνεμος όμως στο ανθρώπινο σώμα έχει και μια άλλη ψυκτική επίδραση, καθώς προκαλεί πιο έντονη εξάτμιση του ιδρώτα (που έστω και ελάχιστος πάντα υπάρχει στο δέρμα), ακόμα και κάτω από στρώματα ρούχων.
Έτσι υπάρχει ένας αντίστοιχος πίνακας (chill factor), που δείχνει πόσο πιο ψυχρό νοιώθουμε τον αέρα, όταν υπάρχει και άνεμος.
Εικόνα 6. Ο πίνακας που δείχνει την επίδραση του ανέμου στην αίσθηση θερμοκρασίας που μας δίνει ο αέρας.
Δεν πρέπει επίσης να ξεχνάμε ότι η ψυκτική επίδραση του νερού είναι 800 φορές πιο έντονη από τον αέρα, γι’ αυτό σε περίπτωση που κάποιος βραχεί σε ψυχρό περιβάλλον είναι απαραίτητο να αλλάξει αμέσως τα βρεγμένα ρούχα του με στεγνά.
Αν όμως εξακολουθεί να βρίσκεται μέσα στο νερό, θα πρέπει να κρατήσει όσα περισσότερα ρούχα μπορεί (φορώντας βέβαια σωσίβιο), καθώς έτσι μειώνεται η ανταλλαγή του νερού που βρίσκεται σε επαφή με το σώμα, και δημιουργείται μια στιβάδα λιγότερο κρύου νερού κοντά στο σώμα (έτσι λειτουργούν και οι ελαστικές στολές των δυτών).
Στην περίπτωση αυτή, δεν πρέπει να ξεχνάμε να έχουμε καλυμμένο και το κεφάλι, από το οποίο χάνεται σημαντικό ποσοστό θερμότητας.
Τελικά, οι ήπιες θερμοκρασίες και τα μέσα ποσοστά υγρασίας δημιουργούν τις καλύτερες συνθήκες για τον άνθρωπο, και δεν μπορούμε να ισχυριστούμε όπως λέει το γνωστό ανέκδοτο για τους στατιστικολόγους, ότι όταν έχουμε το ένα χέρι στη φωτιά και το άλλο στον πάγο, κατά μέσο όρο θα πρέπει να νιώθουμε πολύ καλά!
109. Πώς να σας γυρίσει...μπούμερανγκ.
Συνήθως η έκφραση «γυρίζει μπούμερανγκ» έχει αρνητική σημασία, εκτός αν αφορά ... το πραγματικό μπούμερανγκ, οπότε αυτό είναι και το ζητούμενο.
Κατ’ αρχήν, να διευκρινιστεί ότι το μπούμερανγκ επιστρέφει σ’ αυτόν που το εκτόξευσε με την προφανή προϋπόθεση ότι δεν έχει χτυπήσει τον στόχο του, και τη λιγότερο προφανή... ότι ξέρει καλά τον χειρισμό του.
Το μπούμερανγκ είναι γνωστό ότι είχε αναπτυχθεί πριν πάρα πολλά χρόνια σαν όπλο από τους ιθαγενείς της Αυστραλίας, οι οποίοι βέβαια είχαν καταλήξει στο σχήμα και τον τρόπο χρήσης του από ένα συνδυασμό τυχαίων συμβάντων και πάρα πολλών δοκιμών και αποτυχιών.
Και αυτό επειδή, η Φυσική που εμπλέκεται στην πτήση του μπούμερανγκ χωρίς να είναι δύσκολο να γίνει κατανοητή, δεν είναι φανερή, και χωρίς αυτή την κατανόηση η τροχιά που διαγράφει μοιάζει πράγματι μαγική.
Συνήθως η έκφραση «γυρίζει μπούμερανγκ» έχει αρνητική σημασία, εκτός αν αφορά ... το πραγματικό μπούμερανγκ, οπότε αυτό είναι και το ζητούμενο.
Κατ’ αρχήν, να διευκρινιστεί ότι το μπούμερανγκ επιστρέφει σ’ αυτόν που το εκτόξευσε με την προφανή προϋπόθεση ότι δεν έχει χτυπήσει τον στόχο του, και τη λιγότερο προφανή... ότι ξέρει καλά τον χειρισμό του.
Το μπούμερανγκ είναι γνωστό ότι είχε αναπτυχθεί πριν πάρα πολλά χρόνια σαν όπλο από τους ιθαγενείς της Αυστραλίας, οι οποίοι βέβαια είχαν καταλήξει στο σχήμα και τον τρόπο χρήσης του από ένα συνδυασμό τυχαίων συμβάντων και πάρα πολλών δοκιμών και αποτυχιών.
Και αυτό επειδή, η Φυσική που εμπλέκεται στην πτήση του μπούμερανγκ χωρίς να είναι δύσκολο να γίνει κατανοητή, δεν είναι φανερή, και χωρίς αυτή την κατανόηση η τροχιά που διαγράφει μοιάζει πράγματι μαγική.
Εικόνα 1. Παρατηρείστε στην εικόνα τη διαμόρφωση της διατομής του σώματος του μπούμερανγκ, που μοιάζει με πτέρυγα (ή έλικα) αεροπλάνου. Η κυρτή επιφάνεια είναι προς τα αριστερά του (δεξιόχειρα) ρίπτη.
Όπως φαίνεται στην εικόνα, το σώμα του μπούμερανγκ είναι διαμορφωμένο σαν πτέρυγα αεροπλάνου, και όπως στην πτέρυγα του αεροπλάνου, καθώς κινείται μέσα στον αέρα μετά τη ρίψη του, αναπτύσσεται επάνω του άντωση.
Η άντωση έχει κατεύθυνση προς τα αριστερά του (δεξιόχειρα) ρίπτη, αλλά δεν είναι ομοιόμορφη στα δύο σκέλη του μπούμερανγκ.
Επειδή το σκέλος που βρίσκεται πάνω από τον άξονα περιστροφής του κινείται ταχύτερα μέσα στον αέρα, σε σχέση με το κάτω τμήμα του που «οπισθοχωρεί», η άντωση στο επάνω τμήμα του είναι μεγαλύτερη, και θέλει να κάνει το μπούμερανγκ να γείρει αριστερά.
Μέχρι εδώ τα πράγματα είναι σχετικά απλά.
Τώρα όμως υπεισέρχεται ένα από τα πιο παράξενα φαινόμενα στη φύση, η γυροσκοπική μετάπτωση.
Όπως ενδεχομένως θυμάστε από το Λύκειο, ένα περιστρεφόμενο σώμα θέλει να διατηρήσει τον προσανατολισμό του στο χώρο και το πετυχαίνει, μέχρι κάποιος να σπρώξει τον άξονά του, όχι όμως πολύ κοντά στο κέντρο περιστροφής του.
Τότε το γυροσκόπιο θα αντιδράσει, αλλά με τον πιο παράξενο τρόπο, στρεφόμενο αλλά σαν η δύναμη που ασκήθηκε να είχε εφαρμοστεί παράλληλα μετατοπισμένη κατά 90ο επάνω στην περιφέρειά του και προς την κατεύθυνση περιστροφής του.
Όσο και αν ακούγεται παράλογο έτσι ακριβώς συμβαίνει, και το φαινόμενο της μετάπτωσης έχει παρατηρηθεί από τις σβούρες μέχρι την περιστροφή της Γης.
Εικόνα 2. Φαίνεται ότι αψηφά τους νόμους της βαρύτητας, όμως είναι σύμφωνο με τους νόμους της Φυσικής. Εφόσον ο τροχός περιστρέφεται με αρκετή ταχύτητα, αντί η δύναμη της βαρύτητας να τον τραβήξει προς τα κάτω, κάνει τον άξονα του τροχού να περιστρέφεται οριζόντια γύρω από το σημείο στήριξής του.
Για να επανέλθουμε στο μπούμερανγκ, η μεγαλύτερη άντωση στο επάνω μέρος του και προς τα αριστερά, έχει σαν συνέπεια το μπούμερανγκ να αρχίσει να στρίβει προς τα αριστερά και αυτή η ίδια η στροφή του προς τα αριστερά, πάλι εξαιτίας του φαινομένου της μετάπτωσης, το κάνει επίσης να γυρίζει προοδευτικά την καμπύλη επιφάνεια του προς τα επάνω.
Τώρα όμως συμπεριφέρεται σαν τον μεγάλο έλικα (κύριο στροφείο) ενός ελικόπτερο που κινείται προς τα εμπρός, άρα αποκτά αρκετή άντωση για την τελευταία φάση της πτήσης του, ώστε να καταλήξει οριζόντιο (και αισιόδοξα) στα χέρια του χειριστή του.
Και σαν να μην έφταναν τα παραπάνω, ο άνεμος επηρεάζει σημαντικά την τροχιά του, ειδικά όταν το μπούμερανγκ κινείται στο πιο απομακρυσμένο τμήμα της.
Εικόνα 3. Τυπική τροχιά μπούμερανγκ, που αλλού σκοπεύεις, αλλού πηγαίνει και από αλλού επιστρέφει!
Δεν είναι πράγματι εύκολο να γίνει κατανοητή η πτήση του μπούμερανγκ, και φανταστείτε ότι η επόμενη εποχή στην οποία οι άνθρωποι αντιμετώπισαν ένα πολύ παρόμοιο φαινόμενο, ήταν κατά τον Α’ΠΠ όταν άρχισαν να χρησιμοποιούνται μονοκινητήρια καταδιωκτικά αεροσκάφη.
Τα αεροσκάφη αυτά, που είχαν μεγάλη και βαριά έλικα (και μάλιστα σε κάποιους τύπους περιστρέφονταν και ολόκληρος ο κινητήρας) όχι μόνο είχαν να αντιμετωπίσουν την ασύμμετρη έλξη από την έλικα καθώς κάθονταν με την ουρά χαμηλά στο έδαφος (χρησιμοποιούσαν ουραίο τροχό, ή πέδιλο), αλλά και την εκτροπή από τη γυροσκοπική μετάπτωσή της, τη στιγμή που η ουρά σηκώνονταν από το έδαφος για την απογείωση.
Εικόνα 4. Δύσκολο για το καγκουρό να φανταστεί από πού θα του έλθει το μπούμερανγκ!
Μετά από όλα αυτά μπορεί να αναρωτιέστε πώς οι Αβορίγινες κυνηγοί δεν πέθαναν από την πείνα, χρησιμοποιώντας ένα τόσο δύσκολο όπλο.
Η αλήθεια είναι ότι το μπούμερανγκ που επιστρέφει, χρησιμοποιήθηκε περισσότερο για παιχνίδι και επίδειξη ικανοτήτων, ενώ για το κυνήγι χρησιμοποιούσαν ένα μεγαλύτερο, βαρύτερο και ευθύβολο μπούμερανγκ, αλλά χωρίς τη δυνατότητα επιστροφής.
Ίσως σε τελική ανάλυση, το μπούμερανγκ που επιστρέφει να αναπτύχθηκε από τους λιγότερο ικανούς κυνηγούς, που όμως θα είχαν περισσότερες ευκαιρίες για εξάσκηση!
Εικόνα 5. Μία ωραία φυσική εξήγηση από το διαδίκτυο (https://woodgears.ca/physics/gyro.html ) για το γυροσκοπικό φαινόμενο, που αναπαράγεται παρακάτω:
Φανταστείτε μια σειρά από δορυφόρους που περιστρέφονται σε ισημερινή τροχιά γύρω από τη Γη (μπλε κουκίδες στην πρώτη εικόνα). Για περισσότερη απλοποίηση, φανταστείτε τη Γη ακίνητη.
Θέλοντας να τους αλλάξουμε τροχιά, την ώρα που περνούν από εμπρός μας, τους ωθούμε προς τα επάνω (δεύτερη εικόνα).
Αυτή η ώθηση, θα έχει σαν αποτέλεσμα η τροχιά τους να αποκλίνει προς τα επάνω (κόκκινες κουκίδες), αφού όμως θα έχουν περάσει από εμπρός μας και μάλιστα η μέγιστη απόκλιση θα συμβεί όταν θα έχουν απομακρυνθεί κατά 90 μοίρες προς τη φορά κίνησής τους.
Αν συνεχίσουμε να τους ωθούμε προς τα επάνω κάθε φορά που περνούν από εμπρός μας (ενώ ταυτόχρονα στην αντιδιαμετρική πλευρά της τροχιάς, τους ωθούμε προς τα κάτω), θα καταλήξουν να αλλάξουν τροχιά, όπως δείχνει η τρίτη εικόνα.
Αν τώρα φανταστούμε ότι ενώνουμε τη σειρά των δορυφόρων με ένα στεφάνι, έχουμε έναν σφόνδυλο στον οποίο όταν εφαρμόζουμε ροπή για να τον περιστρέψουμε Βορρά – Νότο εμπρός μας, θα αλλάξει πράγματι κατεύθυνση, αλλά σαν να είχαμε εφαρμόσει τη ροπή μετά από 90 μοίρες προς την κατεύθυνση περιστροφής του.
Εικόνα 6. Στις αρχές του 20ου αιώνα, ό "μάγος" Selbit σε ένα από τα νούμερά του προσκαλούσε στη σκηνή αρκετούς άντρες, ζητώντας τους να ρίξουν στο πλάι ένα μεγάλο κεφάλι τυρί μέσα σε ορισμένο χρόνο. Φυσικά κανείς δεν τα κατάφερνε, επειδή μέσα στο ψεύτικο τυρί κρύβονταν ένας σιδερένιος δίσκος μεγάλης διαμέτρου, που ο Selbit είχε φροντίσει λίγο πριν και εκτός σκηνής να τον περιστρέψει σε υψηλό αριθμό στροφών, δημιουργώντας έτσι ένα ισχυρό γυροσκόπιο.
110. Σελήνη τα..."μέσα έξω".
Αυτή την εντύπωση δίνουν οι κρατήρες της Σελήνης στην παρακάτω φωτογραφία, ότι δηλαδή προεξέχουν από την επιφάνεια της, αντί να βυθίζονται σ' αυτήν.
Πρόκειται όμως για ένα γνωστό "τρικ" που χρησιμοποιεί ο εγκέφαλός μας, "ερμηνεύοντας" αυτό που βλέπουν τα μάτια μας σύμφωνα με την εμπειρία του. Και η εμπειρία του είναι ότι σε μία εικόνα το φως πρέπει να έρχεται από επάνω και οι σκιές να σχηματίζονται προς τα κάτω.
Για του λόγου το αληθές, η παρακάτω φωτογραφία είναι ακριβώς η ίδια με την παραπάνω, απλά έχει περιστραφεί κατά 180 μοίρες (ακόμα και το όνομα του κρατήρα αφέθηκε ανεστραμμένο), ώστε ο φωτισμός να φαίνεται ότι έρχεται από επάνω, οπότε ως δια μαγείας όλα έρχονται στη θέση τους και οι κρατήρες της Σελήνης αποκτούν τη γνωστή τους υφή.
Η αλήθεια είναι ότι το μπούμερανγκ που επιστρέφει, χρησιμοποιήθηκε περισσότερο για παιχνίδι και επίδειξη ικανοτήτων, ενώ για το κυνήγι χρησιμοποιούσαν ένα μεγαλύτερο, βαρύτερο και ευθύβολο μπούμερανγκ, αλλά χωρίς τη δυνατότητα επιστροφής.
Ίσως σε τελική ανάλυση, το μπούμερανγκ που επιστρέφει να αναπτύχθηκε από τους λιγότερο ικανούς κυνηγούς, που όμως θα είχαν περισσότερες ευκαιρίες για εξάσκηση!
Φανταστείτε μια σειρά από δορυφόρους που περιστρέφονται σε ισημερινή τροχιά γύρω από τη Γη (μπλε κουκίδες στην πρώτη εικόνα). Για περισσότερη απλοποίηση, φανταστείτε τη Γη ακίνητη.
Θέλοντας να τους αλλάξουμε τροχιά, την ώρα που περνούν από εμπρός μας, τους ωθούμε προς τα επάνω (δεύτερη εικόνα).
Αυτή η ώθηση, θα έχει σαν αποτέλεσμα η τροχιά τους να αποκλίνει προς τα επάνω (κόκκινες κουκίδες), αφού όμως θα έχουν περάσει από εμπρός μας και μάλιστα η μέγιστη απόκλιση θα συμβεί όταν θα έχουν απομακρυνθεί κατά 90 μοίρες προς τη φορά κίνησής τους.
Αν συνεχίσουμε να τους ωθούμε προς τα επάνω κάθε φορά που περνούν από εμπρός μας (ενώ ταυτόχρονα στην αντιδιαμετρική πλευρά της τροχιάς, τους ωθούμε προς τα κάτω), θα καταλήξουν να αλλάξουν τροχιά, όπως δείχνει η τρίτη εικόνα.
Αν τώρα φανταστούμε ότι ενώνουμε τη σειρά των δορυφόρων με ένα στεφάνι, έχουμε έναν σφόνδυλο στον οποίο όταν εφαρμόζουμε ροπή για να τον περιστρέψουμε Βορρά – Νότο εμπρός μας, θα αλλάξει πράγματι κατεύθυνση, αλλά σαν να είχαμε εφαρμόσει τη ροπή μετά από 90 μοίρες προς την κατεύθυνση περιστροφής του.
Εικόνα 7. Μία πρωτότυπη (δεκαετία 1950!) χρήση του γυροσκοπικού φαινομένου στα πτερύγια σταθεροποίησης του βλήματος αέρος-αέρος AIM-9. Ο τροχίσκος με τις "οδοντώσεις" είναι στην πραγματικότητα ένα γυροσκόπιο που περιστρέφεται στις 100.000 στρ/λεπτό από τη ροή του αέρα και είναι στερεωμένος στο κινητό πτερύγιο που εδράζεται στον άξονα, στα δεξιά της εικόνας, στο πίσω τμήμα του βλήματος. Αν το βλήμα (που κινείται προς τα δεξιά) τείνει να περιστραφεί, τότε το γυροσκόπιο αντιδρά εκτρέποντας το πτερύγιο ώστε να εξαληφθεί η τάση περιστροφής, και όλα αυτά με τελείως μηχανικό τρόπο. Η βασική κατεύθυνση του βλήματος βέβαια, εξασφαλίζεται με πνευματικά κινούμενα πτερύγια στο εμπρός τμήμα του.
ΥΓ1. Ένα ωραίο βίντεο για ένα πειραματικό τρένο "monorail" των αρχών του 20ου αι. σταθεροποιούμενο με δύο μεγάλα γυροσκόπια, μπορείτε να δείτε (με τις αναπόφευκτες διαφημίσεις) εδώ: https://www.youtube.com/watch?v=kUYzuAJeg3M
ΥΓ2. Ένα πολύ ενδιαφέρον βίντεο (στα αγγλικά) που εξηγεί γιατί ένα γυροσκόπιο που περιστρέφεται στην άκρη μιας ράβδου "φαίνεται" ελαφρύτερο, υπάρχει εδώ: https://www.youtube.com/watch?v=tLMpdBjA2SU
Αυτή την εντύπωση δίνουν οι κρατήρες της Σελήνης στην παρακάτω φωτογραφία, ότι δηλαδή προεξέχουν από την επιφάνεια της, αντί να βυθίζονται σ' αυτήν.
Για του λόγου το αληθές, η παρακάτω φωτογραφία είναι ακριβώς η ίδια με την παραπάνω, απλά έχει περιστραφεί κατά 180 μοίρες (ακόμα και το όνομα του κρατήρα αφέθηκε ανεστραμμένο), ώστε ο φωτισμός να φαίνεται ότι έρχεται από επάνω, οπότε ως δια μαγείας όλα έρχονται στη θέση τους και οι κρατήρες της Σελήνης αποκτούν τη γνωστή τους υφή.
Αυτό είναι ένα από τα πολλά παράδοξα που έχουν σχέση με το ότι "άλλο κοιτάζουν τα μάτια και άλλο βλέπει ο εγκέφαλός μας", με το πιο γνωστό παράδειγμα ότι οι εικόνες μέσα στο μάτι μας σχηματίζονται ανεστραμμένες, αλλά ο εγκέφαλος κάνει αυτόματα τη διόρθωση.
Σε πειράματα, άνθρωποι που για μερικές ημέρες φορούσαν ειδικά γυαλιά που ανέστρεφαν την εικόνα, άρχισαν στη συνέχεια να βλέπουν κανονικά (φορώντας πάντα αυτά τα γυαλιά), καθώς ο εγκέφαλος διόρθωνε τη αναστροφή που εισήγαγαν τα γυαλιά.
Είναι επίσης γνωστό, ότι τα δύο μάτια μάς επιτρέπουν την ακριβή εκτίμηση του βάθους, μια ικανότητα που χάνεται βλέποντας με το ένα μόνο μάτι, αν και σ΄ αυτή την περίπτωση μπορούμε να κρίνουμε χοντρικά την απόσταση από το μέγεθος γνωστών αντικειμένων.
Μια αντίστοιχη περίπτωση περιγράφεται στο μυθιστόρημα του Ένγκαρ Άλλαν Πόε "Η Σφίγγα", όπου ο ήρωας έβλεπε ένα έντομο που κινείτο κατά μήκος μιας κλωστής αράχνης πολύ κοντά στο μάτι του, σαν ένα γιγάντιο τρομακτικό τέρας, καθώς είχε χάσει την αίσθηση του βάθους εξαιτίας διαταραχών που είχαν να κάνουν με άγχος, φοβίες και προκαταλήψεις.
Και φυσικά, είναι πολύ γνωστή η ικανότητα του εγκέφαλού μας να συμπληρώνει τα κενά, κάτι που μας επιτρέπει να παρακολουθούμε κινηματογράφο, αλλά από την άλλη πλευρά να παρερμηνεύουμε αφηρημένα σχήματα (παρειδωλία), καθώς ο εγκέφαλός μας αρέσκεται να εντοπίζει οικείες φιγούρες, κάτι προφανώς κρίσιμο για την επιβίωση στα εκατοντάδες χιλιάδες χρόνια της εξέλιξής του.
111. "Φαντάσματα" της Επιστήμης.
Τέτοιο οικείο παράδειγμα είναι η "Φυγόκεντρος" δύναμη, για την οποία υπάρχει ειδική αναφορά στο θέμα Νο9 και στην πραγματικότητα είναι αποτέλεσμα του νόμου της αδράνειας, σύμφωνα με τον οποίο κάθε σώμα κινείται ευθύγραμμα και ομαλά εφόσον δεν ασκούνται επάνω του δυνάμεις.
Παρόμοια υποθετική δύναμη είναι η "Coriolis" που χρησιμοποιείται για να εξηγήσει τις εκτροπές που παρουσιάζονται εξαιτίας των διαφορετικών ταχυτήτων της επιφάνειας της Γης, ανάλογα με το γεωγραφικό πλάτος.
Ένα άλλο παράδειγμα από τα μαθηματικά, είναι το "i", η τετραγωνική ρίζα του -1 που μας επιτρέπει να λύνουμε ασκήσεις συνδυάζοντας διαφορετικές οντότητες, όπως στην περίπτωση της ενεργού και αέργου ισχύος.
Ένα ακόμα παράδειγμα είναι τα "Ταχυόνια", υποθετικά σωματίδια που κινούνται μόνον ταχύτερα από το φως, και γι' αυτόν ακριβώς το λόγο μας επιτρέπουν διανοητικές ασκήσεις που γυρίζουν τον χρόνο προς τα πίσω.
Δεν αναφερόμαστε όμως σε θεωρητικά προβλέψιμα σωματίδια, όπως πχ το σωματίδιο Higgs, για το οποίο απλά μέχρι το 2012 δεν υπήρχαν αρκετά ισχυρά μηχανήματα στο CERN για να το δημιουργήσουν πειραματικά. Με την ευκαιρία, η επόμενη προσπάθεια του CERN μετά από μία ακόμα αναβάθμισή του, είναι η έρευνα για τη φύση της σκοτεινής ύλης.
Ένα άλλο παράδειγμα από τα μαθηματικά, είναι το "i", η τετραγωνική ρίζα του -1 που μας επιτρέπει να λύνουμε ασκήσεις συνδυάζοντας διαφορετικές οντότητες, όπως στην περίπτωση της ενεργού και αέργου ισχύος.
Ένα ακόμα παράδειγμα είναι τα "Ταχυόνια", υποθετικά σωματίδια που κινούνται μόνον ταχύτερα από το φως, και γι' αυτόν ακριβώς το λόγο μας επιτρέπουν διανοητικές ασκήσεις που γυρίζουν τον χρόνο προς τα πίσω.
Δεν αναφερόμαστε όμως σε θεωρητικά προβλέψιμα σωματίδια, όπως πχ το σωματίδιο Higgs, για το οποίο απλά μέχρι το 2012 δεν υπήρχαν αρκετά ισχυρά μηχανήματα στο CERN για να το δημιουργήσουν πειραματικά. Με την ευκαιρία, η επόμενη προσπάθεια του CERN μετά από μία ακόμα αναβάθμισή του, είναι η έρευνα για τη φύση της σκοτεινής ύλης.
112. Σύντηξη και Σχάση.
Τα πλεονεκτήματα της Σύντηξης έναντι της Σχάσης είναι πολλά και πολυδιαφημισμένα. Φυσικά μένει να πραγματοποιηθεί με ελεγχόμενο τρόπο, ενώ μία πρόοδος που ανακοινώθηκε στα τέλη του 2022 είναι ένα πολύ μικρό βήμα προς αυτή την κατεύθυνση.
Εδώ όμως θα εξετάσουμε το πώς προκύπτει το ενεργειακό πλεονέκτημα της Σύντηξης έναντι της Σχάσης.
Είναι φανερό ότι η ενέργεια που παίρνουμε από τη Σύντηξη είναι μεγαλύτερη, ειδικά αν συνυπολογίσουμε και τη διαφορά πυκνότητας των αρχικών υλικών.
Και επιπλέον υπάρχουν τα πλεονεκτήματα της αφθονίας της πρώτης ύλης και της πολύ χαμηλότερης ραδιενέργειας, υπέρ της Σύντηξης. Μένει βέβαια να πραγματοποιηθεί με εκμεταλλεύσιμο τρόπο, κάτι όμως που όπως προαναφέρθηκε δεν είναι ορατό για το άμεσο μέλλον.
*Κάτι αντίστοιχο με τη λανθάνουσα θερμότητα ατμοποίησης, που πρέπει να τη δώσουμε στο νερό για να γίνει ατμός (ίδιας θερμοκρασίας), αλλά την παίρνουμε πίσω με τη συμπύκνωση του ατμού πάλι σε νερό.
Για την πυρηνική ενέργεια, βλέπε και θέμα Νο 40, ενώ για την Ψυχρή Σύντηξη εδώ: https://geometax12.blogspot.com/2023/01/blog-post.html
Επειδή στα αεροπλάνα το κάθε γραμμάριο βάρους μετράει. Έτσι, ενώ την καλύτερη απόδοση οι γεννήτριες και οι μετασχηματιστές την έχουν γύρω στα 50-60Hz, στα 400Hz μπορούν να παράγουν την ίδια ισχύ με πολύ μικρότερο όγκο και βάρος*, ενώ η ελαφρώς μειωμένη απόδοση δεν παίζει τόσο μεγάλο ρόλο. Αντίθετα στα μηχανήματα εδάφους, το βάρος δεν είναι σημαντικός παράγοντας (εκτός από το αρχικό κόστος κατασκευής), αλλά το μήκος είναι (προκειμένου για γραμμές μεταφοράς) οπότε στις περιπτώσεις αυτές έχει επικρατήσει η συχνότητα των 50 ή 60 Hz, ανάλογα με τη χώρα, ή μάλλον με την ήπειρο (εικόνα κάτω).
* Όσο μεγαλύτερη η συχνότητα, τόσο μειώνεται η επιφάνεια της διατομής του πυρήνα που απαιτείται για να δημιουργήσει το ίδιο επαγωγικό αποτέλεσμα στα πηνία. Αν όμως το παρακάνουμε με την αύξηση της συχνότητας, δημιουργούνται προβλήματα από την αύξηση των απωλειών εξαιτίας της υψηλής αυτεπαγωγής, της Η/Μ ακτινοβολίας και του επιδερμικού φαινομένου.
Η Φύση αγαπάει τη σταθερότητα. Κάτι που πιο επιστημονικά αναφέρεται σαν τάση προς αύξηση της εντροπίας σε ένα σύστημα (βλέπε και θέμα Νο53 στο ίδιο άρθρο).
Στην περίπτωση λοιπόν που ένας
μαγνήτης θα προσεγγίσει μια ή περισσότερες σπείρες που είναι συνδεδεμένες σε κλειστό αγώγιμο κύκλωμα,
θα δημιουργηθεί ένα ρεύμα που θα διατρέξει τις σπείρες (πηνία) με τέτοιον τρόπο, ώστε να
μειώσει την επίδραση της διαταραχής, δηλαδή την προσέγγιση του μαγνήτη. Έτσι η
σπείρα λειτουργεί σαν ένας άλλος μαγνήτης, αλλά με τέτοια πολικότητα ώστε να
απωθήσει τον μαγνήτη που πλησιάζει. Γι’αυτό, και η παραγωγή ρεύματος με πηνία
(γεννήτριες), προϋποθέτει τη δαπάνη ενέργειας.
Αντίστοιχα όταν ο μαγνήτης απομακρύνεται, η φορά του ρεύματος είναι τέτοια ώστε το πηνίο να ασκήσει έλξη στον μαγνήτη, άρα πάλι να αντισταθεί στην αλλαγή.
Ένα άλλο παράδειγμα είναι η μαγνητική πυξίδα, που στρέφει έτσι
τη βελόνα της ώστε το μαγνητικό της πεδίο να αντιτίθεται σε αυτό της Γης,
μειώνοντας ουσιαστικά την ένταση του τελευταίου στην πολύ κοντινή περιοχή της.
Παράλληλα, οι αιχμηρές απολήξεις των πυλώνων έπαιζαν τον ρόλο αλεξικέραυνων.
Σήμερα, που τα εργοστάσια φωταερίου έχουν εκλείψει, πολλές τέτοιες κατασκευές (στα αγγλικά Gasholders) διατηρούνται σαν ορόσημα της βιομηχανικής εποχής των αρχών του 20ου αι., ή ενσωματώνονται αρχιτεκτονικά σε σύγχρονες κατασκευές.
116. Το αναγεννητικό φρενάρισμα των ηλεκτρικών αυτοκινήτων.
Το αναγεννητικό φρενάρισμα των ηλεκτρικών αυτοκινήτων αλλά και των υβριδικών, είναι ένα από τα βασικά τους πλεονεκτήματα για την εξοικονόμηση ενέργειας.
Η αρχή λειτουργίας είναι απλή, σχεδόν κάθε ηλεκτρικός κινητήρας μπορεί να δουλέψει και σαν γεννήτρια, αν υπερταχυνθεί από το φορτίο του.
Στη συγκεκριμένη περίπτωση των ηλεκτρικών αυτοκινήτων, αυτό επιτυγχάνεται με τη μείωση της συχνότητας της εναλλασσόμενης τάσης που ο inverter (αντιστροφέας)* εφαρμόζει στον κινητήρα εναλλασσομένου ρεύματος, έτσι ώστε να φαίνεται σαν ο κινητήρας να βρίσκεται σε υπερτάχυνση, οπότε μπαίνει αυτόματα σε κατάσταση φρεναρίσματος. Εννοείται ότι η ταχύτητα του ρότορα του κινητήρα παρακολουθείται με ακρίβεια από το σύστημα ελέγχου της λειτουργίας του.
Μερικά ακόμα ηλεκτρονικά ισχύος προστίθενται στο κύκλωμα (DC/DC converter), ώστε η ανακτώμενη ηλεκτρική ενέργεια να αποκτήσει την κατάλληλη τάση για τη φόρτιση της μπαταρίας κίνησης.
* Ο inverter παράγει εναλλασσόμενη τάση από τη συνεχή της μπαταρίας, μεταβάλλοντας τόσο τη συχνότητα εναλλαγής όσο και την RMS τάση των παλμοσειρών που δημιουργεί (εικόνα κάτω), χρησιμοποιώντας ημιαγωγούς ισχύος IGBT σαν ταχύτατους (μερικές δεκάδες kHz) διακόπτες.
Σήμερα (2023), η δυνατότητα ανάκτησης φτάνει στο 80% περίπου της συνολικής ενέργειας που εκλύεται κατά το φρενάρισμα, που θα πήγαινε χαμένη σε θερμότητα και σε φθορά των υλικών τριβής.
Όμως υπάρχουν ορισμένοι περιορισμοί. Ένα φρενάρισμα πχ από τα 110km/h μέχρι τη στάση ενός αυτοκινήτου 2 τόνων, εκλύει ενέργεια περίπου 1000kJ ή περίπου 0.3 kWh. Αν το φρενάρισμα είναι έντονο και ολοκληρωθεί (για παράδειγμα) μέσα σε 3s, αντιστοιχεί σε ισχύ 360kW* την οποία θα πρέπει να διαχειριστεί ο ηλεκτρικός κινητήρας και τα τα ηλεκτρονικά του.
*Ο υπολογισμός έγινε με το 100% της ενέργειας πέδησης, καθώς δεν είναι σαφές σε πιο σημείο "χάνεται" το 20% της ενέργειας, οπότε ενδέχεται το σύστημα να πρέπει να διαχειριστεί και αυτό το κομμάτι.
Είναι όμως προφανές, ότι για να μπορέσει να γίνει αυτή η ανάκτηση, η μπαταρία δεν θα πρέπει να είναι πλήρως φορτισμένη, αλλά να έχει ένα μικρό περιθώριο φόρτισης*.
Επίσης, η ισχύς του ηλεκτρικού κινητήρα (που για την ανάκτηση θα δουλέψει σαν γεννήτρια) και των ηλεκτρονικών του, θα πρέπει να επαρκεί για να διαχειριστεί όλη αυτήν την ισχύ, που σημαίνει ότι θα πρόκειται εξ αρχής για ένα αυτοκίνητο μεγάλης ισχύος. Αυτό ισχύει βέβαια, προκειμένου να αξιοποιηθεί το μέγιστο δυνατό ποσοστό ανάκτησης ενέργειας ενός πολύ δυνατού φρεναρίσματος, όπως προαναφέρθηκε.
Δοκιμές πάντως έχουν δείξει ότι στην πράξη η ανάκτηση ενέργειας φρεναρίσματος βρίσκεται κοντά στο 50%, το οποίο μειώνεται ακόμα περισσότερο στα απότομα φρεναρίσματα, όπου τα κλασικά φρένα έχουν πολύ μεγαλύτερη συμμετοχή στην επιβράδυνση του αυτοκινήτου.
* Η Tesla για παράδειγμα, προτείνει φόρτιση της μπαταρίας μέχρι το 90%, τόσο για να υπάρχει περιθώριο για αναγεννητική πέδηση όσο και για να μην καταπονείται η μπαταρία ούτε να παρατείνεται με μικρό όφελος ο χρόνος φόρτισης (ειδικά στους δημόσιους φορτιστές).
117. Και λίγα για τους κινητήρες των ηλεκτρικών αυτοκινήτων.
Οι κινητήρες των σύγχρονων ηλεκτρικών αυτοκινήτων είναι γενικά δύο τύπων: Είτε ασύγχρονοι (συνήθως παλαιότερα), είτε σύγχρονοι μόνιμου μαγνήτη (πιο πρόσφατα).
Αν όμως σ’ ένα ηλεκτρικό αυτοκίνητο υπάρχουν δύο κινητήρες, ένας σε κάθε άξονα, συνήθως επιλέγονται διαφορετικού τύπου, δηλαδή ένας ασύγχρονος επαγωγικός (κλωβού), εικόνα 1,
Εικόνα 1. Τυπικός ασύγχρονος κινητήρας.
και ένας σύγχρονος μόνιμου μαγνήτη, ή
συνηθέστερα ενός συνδυασμού μόνιμων μαγνητών και μαγνητικής
υστέρησης (reluctance). Ο τελευταίος τύπος, που αναφέρεται στα
αγγλικά σαν PMSynRM (Permanent Magnets
Synchronous Reluctance Motor) θα μπορούσε να
χαρακτηριστεί και σαν «δύο κινητήρες σε έναν» (εικόνα 2).
Ο λόγος είναι ότι κάθε κινητήρας έχει τα
πλεονεκτήματά του, με τον επαγωγικό να είναι οικονομικότερος και με μεγάλη ροπή
εκκίνησης (κάτι που το εξασφαλίζουν τα ηλεκτρονικά του), ενώ αυτός του μόνιμου
μαγνήτη έχει μεγαλύτερη απόδοση.
Έτσι, ενώ στην επιτάχυνση ή όταν χρειάζεται
τετρακίνηση ενεργοποιούνται και οι δύο κινητήρες, σε συνθήκες ταξιδιού ενεργοποιείται κυρίως
ο κινητήρας μόνιμου μαγνήτη για να επιτευχθεί συνολικά μεγαλύτερη αυτονομία.
Μία σχετικά πρόσφατη εξέλιξη στους κινητήρες
της Tesla είναι ένα χιτώνιο ανθρακονημάτων (plaid)
που περιβάλει πολύ σφικτά τον ρότορα ώστε να αντέχει σε υψηλούς ρυθμούς
περιστροφής, καθώς ο πυρήνας του (συνδυασμός μόνιμων μαγνητών και υστέρησης)
αποτελείται από διακριτά τμήματα (εικόνα 3).
Ενδιαφέρον πάντως έχει, ότι σε κάθε περίπτωση οι στάτες είναι ουσιαστικά πανομοιότυποι, με τυπικό τριφασικό τύλιγμα (αλλάζει ενδεχομένως η τεχνική των τυλιγμάτων, εικόνα 4), ενώ οι διαφοροποιήσεις στους κινητήρες αφορούν βασικά τους ρότορές τους.
Εξίσου πανομοιότυπα είναι και τα ηλεκτρονικά των κινητήρων (ισχύει κυρίως για την περίπτωση των Tesla).
Υπάρχει επίσης το ενδεχόμενο να υπάρχουν στον
ίδιο άξονα (συνήθως στον πίσω) δύο κινητήρες. Σε αυτή την περίπτωση προφανώς θα
είναι πανομοιότυποι, οπότε όχι μόνο δεν χρειάζεται διαφορικό αλλά μπορούν να
χρησιμοποιηθούν και για “torque vectoring”,
να «σπρώχνει» δηλαδή σε μία στροφή ο εξωτερικός κινητήρας περισσότερο, για
καλύτερη συμπεριφορά του αυτοκινήτου στις στροφές.
Υπάρχει ακόμα και η περίπτωση ύπαρξης και τρίτου κινητήρα, στον άλλον άξονα (με χρήση διαφορικού φυσικά), και η Tesla έχει τουλάχιστον δύο μοντέλα με αυτή τη διάταξη.
Στο ίδιο blog, στο ΥΓ3 του link: https://geometax12.blogspot.com/2023/02/blog-post_19.html, μπορείτε να βρείτε τα βασικά για τη φόρτιση των ηλεκτρικών αυτοκινήτων.
118. Τρία διαφορετικά...διαφορικά (Variomatic, Torsen και Επικυκλικό).
Μία διευκρίνιση εξ' αρχής. Το Variomatic δεν είναι διαφορικό, αλλά σύστημα συνεχώς μεταβαλλόμενης σχέσης μετάδοσης κίνησης, χωρίς τη χρήση διαφορετικών σχέσεων γραναζιών.
Όμως το...λογοπαίγνιο δεν είναι εντελώς εκτός τόπου, μιας και το σύστημα Variomatic καταργούσε...το διαφορικό (τουλάχιστον στις αρχικές εκδόσεις του). Το οποίο (κλασικό) διαφορικό δεν θα αναλυθεί εδώ, θεωρώντας τη λειτουργία του αρκετά γνωστή, σε αντίθεση με το Variomatic που είναι πολύ λιγότερο γνωστό.
Σήμερα η ιδέα αυτή επιβιώνει σε ένα ζευγάρι τροχαλιών που λειτουργεί σαν αυτόματο κιβώτιο ταχυτήτων χωρίς διακριτές σχέσεις γραναζιών, και με μεταλλική αλυσίδα αντί του ιμάντα, με το όνομα CVT (Continuously Variable Transmission), και χρησιμοποιείται συνήθως από Ιάπωνες και Κορεάτες κατασκευαστές αυτοκινήτων.
Το Torsen (Torque-Sensing) είναι ένα διαφορικό που μοιάζει στη βασική αρχή λειτουργία του με το κλασικό, αλλά τα γρανάζια που μοιράζουν την κίνηση δεξιά-αριστερά (Worm wheels, στην εικόνα επάνω), είναι "κομμένα" με τέτοια γωνία και σε εμπλοκή μεταξύ τους (μέσω των Spur gears), που η ροπή μπορεί να μεταφέρεται σχεδόν ισόποσα προς τους τροχούς ακόμα και αν οι τροχοί τείνουν να κινηθούν με διαφορετική ταχύτητα εξαιτίας μιας στροφής πχ. Αν όμως ένας τροχός βρεθεί στον αέρα, δεν "κλέβει" την κίνηση (και τη ροπή) από τον άλλο γυρίζοντας "τρελά" όπως στο απλό διαφορικό, γιατί η κίνηση (εξαιτίας της γωνίας των γραναζιών) δεν μπορεί να μεταδοθεί προς την αντίθετη κατεύθυνση. 
Παρά τις πολλές διαφορετικές χρήσεις του, η αρχή λειτουργίας είναι μάλλον απλή, όπως φαίνεται και στην εικόνα επάνω και βασίζεται στο ότι υπάρχουν τρία αλληλοεμπλεκόμενα σετ γραναζιών.
Το Torsen, αν και αμερικάνικη εφεύρεση, έγινε γνωστό από τη χρήση του σαν κεντρικό διαφορικό στα Audi Quattro στους αγώνες ράλι τη δεκαετία του ΄80, αποτελώντας καθοριστικό παράγοντα της εξαιρετικής επιτυχίας τους.
Το Επικυκλικό, μπορεί να είναι ένα (κεντρικό συνήθως) διαφορικό, μπορεί επίσης να αποτελεί τμήμα ενός αυτόματου κιβωτίου ταχυτήτων, ή ακόμα να είναι μέρος ενός μηχανικού συστήματος κατευθυνόμενης ώσης (Torque Vectoring) τοποθετημένο στις δύο πλευρές ενός συμβατικού διαφορικού.
Συνεπώς αρκεί κάθε φορά να φρενάρει κάποιο απ' αυτά, ώστε η κίνηση να μεταφέρεται μέσα από τους άξονες των άλλων δύο.
Το πρωτοποριακό σύστημα της Toyota, "Hybrid Synergy Drive" (εικόνα επάνω) χρησιμοποιεί την αρχή του επικυκλικού μηχανισμού (κέντρο της εικόνας) για να μεταφέρει την ισχύ στους τροχούς, ρυθμίζοντας συνεχώς και με ομαλό τρόπο την κατανομή της ανάμεσα σε έναν θερμικό κινητήρα (PETROL) και δύο ηλεκτρικούς κινητήρες /γεννήτριες (MG1, MG2), ώστε να φορτίζει σε κατάλληλες στιγμές και τη μπαταρία κίνησης.
Έτσι, για την διοχέτευση της ισχύος δεν χρειάζεται να φρενάρει μηχανικά κάποιο στοιχείο του επικυκλικού μηχανισμού, αλλά απλά να μπαίνει σε λειτουργία γεννήτριας.
119. Γιατί ο συντελεστής θερμικής διαστολής όγκου (β) είναι (μόνο) τριπλάσιος από τον αντίστοιχο συντελεστή γραμμικής διαστολής (α) για το ίδιο υλικό;
Αυτή η ιδιαιτερότητα (που εξηγείται βέβαια μαθηματικά και αφορά απλοποιήσεις) συμβαίνει επειδή ο συντελεστής γραμμικής διαστολής είναι ένα πάρα πολύ μικρό ποσοστό του αρχικού μήκους, οπότε είναι σαν σε κάθε μία από τις τρείς ελεύθερες πλευρές ενός (υποθετικού) κύβου "κολλημένου" στην αρχή των αξόνων, να προσθέσουμε ένα πολύ λεπτό στρώμα από το υλικό αυτό, εξαιτίας της διαστολής του.
Επειδή το στρώμα είναι πολύ λεπτό και αφορά τις τρείς πλευρές του κύβου, μπορούμε να θεωρήσουμε τον επιπλέον όγκο σαν τον όγκο των τριών στρωμάτων, παραλείποντας τον ελάχιστα παραπάνω όγκο που προκύπτει από τη διαστολή στα σημεία των ακμών.
120. Ένας "μύθος" για τους ηλεκτροκινητήρες συνεχούς ρεύματος.
Ο οποίος είναι, ότι αν σ' έναν ηλεκτροκινητήρα συνεχούς ρεύματος με παράλληλη ή ξένη διέγερση (εικόνα επάνω) διακοπεί το κύκλωμα της διέγερσης, ο ηλεκτροκινητήρας θα υπερταχυνθεί, κινδυνεύοντας να πάθει ζημιά.
Η άποψη αυτή υπάρχει, επειδή οι στροφές (n) ενός ηλεκτροκινητήρα συνεχούς ρεύματος, εξαρτώνται από το μέγεθος της μαγνητικής ροής της διέγερσής του (Φ), σε αντίστροφη αναλογία.
Δηλαδή ισχύει:
n = k1 Ε / Φ (το k1 είναι σταθερός συντελεστής, και Ε είναι η τάση που αναπτύσσεται εξ επαγωγής στον δρομέα ή ρότορα, εφόσον η Φ δεν είναι μηδενική).
Όμως ισχύει και ένας άλλος τύπος σ' αυτή την περίπτωση:
Τ = k2 Φ Ι (όπου το k2 είναι σταθερός συντελεστής, και το Ι το ρεύμα του ρότορα).
Είναι φανερό, ότι ναι μεν οι στροφές (n) τείνουν "στο άπειρο" εξαιτίας της πρώτης σχέσης όταν το Φ μηδενιστεί, αλλά επίσης η ροπή (Τ) τείνει στο μηδέν, εξαιτίας της δεύτερης σχέσης, οπότε ο κινητήρας μάλλον θα σταματήσει, ειδικά αν έχει κάποιο φορτίο.
Επίσης στην περίπτωση αυτή, καθώς δεν αναπτύσσεται (αντίστροφη) τάση E εξ επαγωγής στον ρότορα, το ρεύμα Ι αυξάνεται πολύ, και αν δεν λειτουργήσει κάποια συσκευή προστασίας από την υπερένταση ο κινητήρας κινδυνεύει να καεί.
Βέβαια, ο μύθος δεν ισχύει ούτως ή άλλως για τους κινητήρες διέγερσης σειράς, όπου εκεί το ρεύμα Ι διακόπτεται μαζί με το ρεύμα της διέγερσης.
121. kilo ή Kilo;
Ίσως θα έχετε παρατηρήσει ότι γενικά τα πολλαπλάσια των μονάδων γράφονται με κεφαλαία γράμματα (πχ MW, GeV κλπ), ενώ τα υποπολλαπλάσια με μικρά (πχ mg, μF κλπ).
Υπάρχει όμως μία πολύ γνωστή εξαίρεση: το kilo, που σύμφωνα με τα παραπάνω θα έπρεπε να γράφεται ως Kilo, και παρόλα αυτά γράφουμε: km, kW κλπ.
Ο κανόνας όμως είναι ο παρακάτω, ή μάλλον οι παρακάτω:
-Αν η μονάδα είναι όνομα επιστήμονα, γράφεται με κεφαλαίο, πχ Volt, Ampere, Watt, Kelvin, Tesla κλπ, αλλιώς με μικρά, πχ calorie, meter, second, gram κλπ.
-Για τα πολλαπλάσια των μονάδων χρησιμοποιούνται τα αρχικά ελληνικών λατινοποιημένων λέξεων, πχ deka, hecto, kilo, mega, giga, tera κλπ, ενώ για τα υποπολλαπλάσια τα αρχικά λατινικών, πχ deci, centi, milli, micro, nano, pico κλπ (κάποιες λατινικές λέξεις βέβαια είναι και αυτές ελληνικής προέλευσης).
-Αν δεν υπάρχει μονάδα που να χρησιμοποιεί κάποιο κεφαλαίο γράμμα, τότε προτιμάμε το αντίστοιχο πολλαπλάσιο, εφόσον χρησιμοποιεί αυτό το γράμμα, να το γράφουμε με κεφαλαίο και τα υποπολλαπλάσια με μικρό. Συνεπώς, καθώς υπάρχει το Kelvin, το kilo το γράφουμε με k, και επιπλέον το Κ χρησιμοποιείται ειδικά στην πληροφορική για να δηλώσει το 1024.
Μια άλλη "παρατυπία" είναι το micro, που ενώ θα έπρεπε να γράφεται με "μ" για να ξεχωρίζει από το milli, συχνά εξαιτίας της αδυναμίας για ελληνικούς χαρακτήρες, γράφεται σαν "u", πχ uF.
Αντίστοιχα, το σύμβολο του Ohm είναι το "Ω", αλλά για τον ίδιο με τον παραπάνω λόγο συχνά γράφεται με το πλήρες όνομα: "Ohm".
Μία "βολική" λύση που χρησιμοποιείται συχνότερα στην επιστήμη, είναι τα μεγάλα πολλαπλάσια ή υποπολλαπλάσια να γράφονται σαν δυνάμεις του 10, οπότε το θέμα (και οι υπολογισμοί) απλοποιούνται.
122. Η μοτοσυκλέτα που τρέμει (wobble).
Μερικές φορές, ενώ μια μοτοσυκλέτα κινείται με αρκετά μεγάλη ταχύτητα, μπορεί να συμβεί μια διαταραχή που καταλήγει σε μία έντονη ταλάντωση δεξιά-αριστερά του τιμονιού και του εμπρός τροχού, που μπορεί να γίνει τόσο έντονη ώστε να οδηγήσει μέχρι και σε πτώση του αναβάτη.
Η εμφάνιση αυτού του συντονισμού συμβαίνει συνήθως σε συγκεκριμένη ταχύτητα για κάθε συνδυασμό μοτοσυκλέτας - αναβάτη.
Υπάρχουν διάφορες αιτίες που συνεισφέρουν στο φαινόμενο αυτό, με βασικές το "μαλακό" ή ελαφρά στραβό πλαίσιο, τα δυναμικά αζυγοστάθμιστα ή ανομοιόμορφα φθαρμένα λάστιχα, τζόγο στο σύστημα του τιμονιού κλπ. Επίσης μπορεί να συμβεί από μεγάλη ή απότομη εφαρμογή ισχύος που τείνει να ανασηκώσει τον εμπρός τροχό και ο αναβάτης να προσπαθήσει να κρατήσει την ισορροπία του στρίβοντας το τιμόνι.
Γιατί όμως κατ' αρχήν δημιουργείται αυτή η ταλάντωση;
Η ρίζα της βρίσκεται στο γυροσκοπικό φαινόμενο (βλ. θέμα 109) των τροχών και ειδικά του εμπρός τροχού. Μάλιστα είναι χαρακτηριστικό ότι παρουσιάζεται όταν η μοτοσυκλέτα κινείται σε ευθεία, παρά σε στροφή.
Κατά την άποψη του γράφοντα, το φαινόμενο ξεκινά από μία ανεπαίσθητη και επίπεδη (δηλαδή χωρίς κλίση της μοτοσυκλέτας) στροφή του τιμονιού, για οποιονδήποτε λόγο. Αν για παράδειγμα το τιμόνι στραφεί ελάχιστα δεξιά χωρίς όμως να έχει γύρει η μοτοσυκλέτα (όπως συμβαίνει όταν ο αναβάτης προετοιμάζεται για στροφή), τότε εξαιτίας του γυροσκοπικού φαινομένου (αλλά και της αδρανειακής δύναμης "φυγοκέντρου") δημιουργείται δύναμη στο επάνω μέρος του τροχού (αλλά και στον αναβάτη) που τον σπρώχνει προς τα αριστερά. Αυτό το αντιλαμβάνεται ασυναίσθητα ο αναβάτης που γυρίζει ελάχιστα το τιμόνι του αριστερά για να ισορροπήσει, και τώρα το φαινόμενο αντιστρέφεται σπρώχνοντάς τον προς τα δεξιά, και ο κύκλος επαναλαμβάνεται αυτο-ενισχυόμενος, μέχρι την πτώση ή μέχρι ο αναβάτης να αντιδράσει σωστά.
Το τελευταίο γίνεται χαλαρώνοντας λίγο τα χέρια του, σκύβοντας επάνω στο τεπόζιτο (χαμήλωμα και μεταφορά του κέντρου του βάρους προς τα εμπρός) και μειώνοντας την ταχύτητα χρησιμοποιώντας ελαφρά μόνον το πίσω φρένο. Παράλληλα, ένα αμορτισέρ τιμονιού θα μπορούσε να μειώσει ή και να εξαλείψει το φαινόμενο.
Εννοείται ότι θα πρέπει περιοδικά να ελέγχει τη μοτοσυκλέτα του για τους παράγοντες που προαναφέρθηκαν και ενισχύουν το φαινόμενο αυτό.
Παρατήρηση: Για να μειωθούν οι γυροσκοπικές δυνάμεις, κάποιες μοτοσυκλέτες έχουν τον κινητήρα τοποθετημένο εγκάρσια με τον στροφαλοφόρο άξονα να γυρίζει αντίθετα από τη φορά περιστροφής των τροχών.
123. Μία περίεργη καμπύλη (καμπύλη του Paschen).
Η παραπάνω καμπύλη δείχνει την τάση διάσπασης στον άερα (κατακόρυφος άξονας) με μεταβαλόμενη απόσταση ηλεκτροδίων και μεταβαλόμενη πίεση αέρα (οριζόντιος άξονας).
Μάλιστα, ο οριζόντιος άξονας είναι ουσιαστικά το γινόμενο της πίεσης επί την απόσταση (pd), αλλά για απλοποίηση ας θεωρήσουμε την απόσταση των ηλεκτροδίων σταθερή, οπότε είναι μόνον η πίεση που μεταβάλεται.
Πριν πάμε στην εξήγηση, αξίζει να αναφερθεί ότι αυτή η καμπύλη δείχνει γιατί σε αεροπλάνα που πετούν σε μεγάλο ύψος και χρησιμοποιούν εμβολοφόρους κινητήρες (βενζίνης) απαιτείται το σύστημα παραγωγής σπινθήρων (μανιατό) να βρίσκεται σε υπερπίεση. Ο λόγος είναι, ότι καθώς η ατμοσφαιρική πίεση μειώνεται, άρα μετακινούμαστε από τη δεξιά πλευρά της καμπύλης (ατμοσφαιρική, κοντά στη αιχμή του βέλους) προς το ελάχιστο σημείο της (κόκκινο, που αντιστοιχεί σε υψόμετρο περίπου 30km για διάκενο σπινθηρισμού 10mm), η τάση διάσπασης του αέρα μειώνεται οπότε οι σπινθήρες που παράγονται από τα μανιατό μπορούν εύκολα να διαρρεύσουν προς το περίβλημά τους, αντί να κατευθυνθούν μέσα από τα καλώδια υψηλής τάσης προς τα μπουζί, με αποτέλεσμα η μηχανή να κάνει "διακοπές".
Η προφανής λύση είναι να γίνουν τα μανιατό αεροστεγή και να μπουν σε υπερπίεση που παράγεται ήδη από τους κινητήρες, μια και για να λειτουργήσουν οι τελευταίοι αποτελεσματικά σε μεγάλο υψόμετρο χρειάζονται σύστημα υπερσυμπίεσης για τον αέρα εισαγωγής.
Όπως όμως κάθε ηλεκτρολόγος και φυσικός γνωρίζει, το καλύτερο μονωτικό για θερμότητα και ηλεκτρισμό είναι το κενό, οπότε εδώ μοιάζει να υπάρχει μια αντίφαση. Η "παρεξήγηση" αυτή λύνεται, αν κοιτάξει κάποιος το αριστερό μέρος της καμπύλης, όπου η τάση διάσπασης ανεβαίνει και μάλιστα γρήγορα, καθώς η πίεση πλησιάζει αυτή του κενού.
Το ενδιαφέρον είναι η εξήγηση αυτής της περίεργης συμπεριφοράς των σπινθήρων.
Η οποία έχει σχέση με το πώς ο σπινθήρας μεταπηδάει από μόριο σε μόριο, ή μάλλον από τα ηλεκτρόνια της εξωτερικής στοιβάδας των ατόμων ενός μορίου σε ένα άλλο.
Μοιάζει λοιπόν, ότι η μετάβαση αυτή να γίνεται πιο εύκολα όταν τα μόρια έχουν μια σχετικά μικρή απόσταση μεταξύ τους (μέτρια πίεση), αλλά όχι πολύ μικρή (υψηλή πίεση) επειδή τότε η κίνηση των ηλεκτρονίων "φρενάρεται" από τις συχνές συγκρούσεις, ούτε όμως και πολύ μεγάλη απόσταση (πολύ χαμηλή πίεση) επειδή τότε λιγότερα μόρια είναι διαθέσιμα για να ολοκληρωθούν τα βήματα του σπινθήρα.
ΥΓ. Το φαινόμενο Paschen μοιάζει κάπως με το (θερμικό όμως) φαινόμενο που κινεί τον μύλο του Crookes (βλ. https://geometax12.blogspot.com/2019/01/ranque-hilsch-crookes.html) και το οποίο δουλεύει βέλτιστα σε πίεση μόλις 1Pa.
124. Μια ατίθαση πεταλούδα (φαινόμενο Dzhanibekov).
Όπου ενδιάμεσος άξονας είναι ένας δεύτερος (σε σύνολο τριών) φυσικός άξονας περιστροφής ενός σώματος γύρω από τον εαυτό του. Για παράδειγμα, μία σφαίρα, έχει έναν άξονα περιστροφής, που περνάει από οποιαδήποτε διάμετρό της και συμπίπτει με τον άξονα συμμετρίας της. Ένα δακτυλίδι, έχει δύο φυσικούς άξονες περιστροφής, έναν που περνάει από οποιαδήποτε διάμετρό του και έναν που περνάει από άξονα κάθετο στο κέντρο του, που αμφότεροι είναι και άξονες συμμετρίας. Στην περίπτωση του δακτυλιδιού, είναι επίσης φανερό ότι ο δεύτερος (κάθετος) άξονας παρουσιάζει μεγαλύτερη ροπή αδράνειας από τον πρώτο, καθώς όλη η μάζα του δακτυλιδιού βρίσκαται όσο το δυνατόν πιο απομακρυσμένη από τον άξονα αυτόν.
Σώματα όμως μόνον με έναν άξονα συμμετρίας, όπως πχ μία ρακέτα του τένις (και το παράδειγμα δεν είναι τυχαίο) ή το περίφημο παξιμάδι-πεταλούδα (απ' όπου ξεκίνησαν όλα), έχουν και έναν τρίτο φυσικό άξονα περιστροφής, με τιμή ροπής αδράνειας ενδιάμεση των δύο άλλων αξόνων, που προφανώς ονομάζεται "ενδιάμεσος άξονας".
Το φαινόμενο παρατηρήθηκε για πρώτη φορά το 1985 από τον Σοβιετικό (τότε) κοσμοναύτη Vlad. Dzhanibekov στο διαστημικό σταθμό Salyut 7, καθώς ξεβίδωσε με φόρα ένα παξιμάδι-πεταλούδα που η έλλειψη βαρύτητας το έκανε να συνεχίσει να περιστρέφεται καθώς αποκακρύνονταν από τη βίδα του, αλλά (έκπληξη!) άρχισε επίσης να "τουμπάρει" περιοδικά παραμένοντας παρόλα αυτά στον άξονα περιστροφής του.
Δεν θα δώσουμε εδώ την εξήγηση, αλλά θα παραπέμψουμε στο πολύ καλό βίντεο παρακάτω, σε καλά αγγλικά και με ενδιαφέροντα "παραλειπόμενα": https://www.youtube.com/watch?v=1VPfZ_XzisU
Και μία παρατήρηση σχετικά με το βίντεο. Η περιστροφή του παξιμαδιού-πεταλούδα στο animation, δείχνεται ανάποδη απ΄ αυτήν που προκύπτει από το ξεβίδωμα σε σχέση με την κίνησή της.
125. Ένα ιδιαίτερο "ελατήριο".
125. Ένα ιδιαίτερο "ελατήριο".
Όλοι το ξέρουμε, όλοι έχουμε χρειαστεί τις "υπηρεσίες" του, αλλά λίγοι μάλλον ξέρουν πώς ακριβώς δουλεύει. Πρόκειται για το (μάλλον "τα", αφού σχεδόν πάντα είναι ζευγάρι) "αμορτισέρ" που στηρίζουν την πόρτα του πορτ μπαγκάζ στα περισσότερα αυτοκίνητα, αλλά και σε πολλές άλλες εφαρμογές όπου ένα βάρος πρέπει να υποστηριχτεί.
Η λέξη "αμορτισέρ" είναι σε εισαγωγικά, επειδή παρόλη την επιφανειακή ομοιότητά τους με αμορτισέρ, δεν είναι ακριβώς αμορτισέρ (ο ρόλος των οποίων είναι να αποσβένουν μια ταλάντωση), αλλά συμπεριφέρονται κυρίως σαν ελατήρια αερίου. Και πάλι όμως δεν δουλεύουν με τη συμπίεση του αερίου από ένα έμβολο, αλλά με την πίεση που ασκείται στην επιφάνεια που αντιστοιχεί στο μπράτσο τους.
Αν όλο αυτό μοιάζει κάπως δυσνόητο, η εικόνα παρακάτω θα βοηθήσει.
Αυτό που προσέχει κάποιος αμέσως είναι η τρύπα στο έμβολο (piston), που μοιάζει να το καταργεί! Και πράγματι o ρόλος αυτού του εμβόλου δεν είναι να συμπιέζει το αέριο (συνήθως άζωτο), αλλά αποτελεί απλά έναν οδηγό για την άκρη του μπράτσου (rod) μέσα στον κύλινδρο.
Είναι φανερό, ότι εξαιτίας της τρύπας επικρατεί η ίδια πίεση και από τις δύο πλευρές του εμβόλου, και είναι μόνο η διαφορά των επιφανειών (δηλαδή ουσιαστικά η επιφάνεια της τομής του μπράτσου) που επί την πίεση, μας δίνει τη δύναμη που ασκεί το μπράτσο, φυσικά προς την κατεύθυνση της έκτασής του.
Συνήθως η πίεση του αερίου είναι μερικές δεκάδες bar, η οποία βέβαια αυξάνεται όσο το μπράτσο εισέρχεται μέσα στον κύλινδρο, αλλά η όλη διάταξη δίνει αρκετά μεγάλη διαδρομή με σχετικά μικρή αύξηση της δύναμης, κάτι που δεν θα μπορούσε να επιτευχθεί με ένα κλασικό έμβολο αερίου.
Τελικά, και παρόλα όσα προαναφέρθηκαν, υπάρχει μία ποσότητα λαδιού μέσα στον κύλινδρο, τόσο για τη λίπανση της τσιμούχας στο μπράτσο όσο και για την απόσβεση των απότομων κινήσεων, οπότε τελικά είναι και λίγο αμορτισέρ.
Πρόκειται για τα Yakhchal, ("πηγάδια πάγου", στα περσικά), στην ευρύτερη περιοχή της Περσίας προφανώς, που από την αρχαιότητα παρήγαγαν και διατηρούσαν πάγο όλες τις εποχές του χρόνου και μάλιστα χωρίς δαπάνη ενέργειας.
Η ψύξη αυτή δημιουργεί πάγο, ο οποίο κόβεται και στη συνέχεια αποθηκεύεται στον κεντρικό τεράστιο κωνικό χώρο, που είναι χτισμένος από ένα μίγμα φυσικών υλικών που τα κάνει αδιάβροχα και θερμοάντοχα. Χαρακτηριστικά, οι τοίχοι της κωνικής αυτής "καμινάδας" έχουν πάχος στη βάση τους που φτάνει τα 2m, ενώ στην κορυφή υπάρχει μικρή οπή για να φεύγει ο αέρας που έχει ζεσταθεί.
Καθώς σήμερα η ανάγκη για παρασκευή πάγου με αυτόν το τρόπο είναι πλέον περιορισμένη, παρόλο που υπάρχουν ακόμα μερικά λειτουργικά yakhchal, ένα παρόμοιο σύστημα που χρησιμοποιεί υπόγεια κανάλια νερού (Quanat ή Kanat) και ροή αέρα που διοχετεύεται από επάνω τους και ψύχεται, εξακολουθεί να χρησιμοποιείται για να κρατάει δροοσερό το εσωτερικό μιας κατοικίας.
127. Το "υγρό" με το μεγαλύτερο ιξώδες.
Ταυτόχρονα αποτελεί το πείραμα με τη μεγαλύτερη διάρκεια στον κόσμο!
Το πείραμα αποσκοπούσε να δείξει ότι η πίσσα είναι ρευστό σε θερμοκρασία περιβάλλοντος, και το απέδειξε καθώς 10 (γιγάντιες) σταγόνες έχουν πέσει μέχρι σήμερα.
Έχει ενδιαφέρον, ότι το συγκεκριμένο δεν αποτελεί ούτε το μοναδικό ούτε το παλαιότερο παρόμοιο πείραμα στον κόσμο, είναι όμως το πιο διάσημο!
Με την ευκαιρία, κάποτε πίστευαν ότι και το γυαλί (σε θερμοκρασία περιβάλλοντος) έρρεε αν και πάρα πολύ αργά, παρατηρώντας ότι σε μεσαιωνικά τζάμια το κάτω μέρος εμφανίζονταν συχνά παχύτερο. Κάτι που αποδείχτηκε ότι δεν ίσχυε, και η διαφορά στο πάχος αποδόθηκε στην πρωτόγονη μέθοδο κατασκευής τους και στο γεγονός ότι οι τεχνίτες θα προτιμούσαν να τοποθετούν το παχύτερο μέρος, κάτω.
ΥΓ. Για άλλα μακροχρόνια πειράματα, από τα πρώτα βήματα της επιστήμης, κοιτάξτε το θέμα 28.
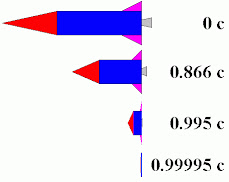
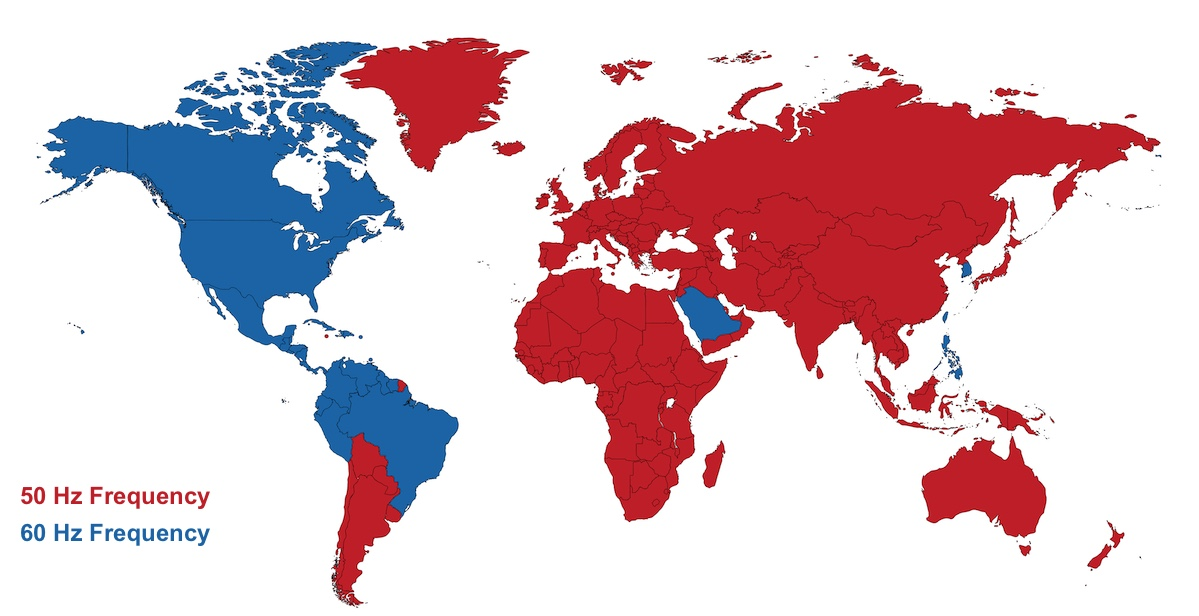
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου