Απλά κουίζ Φυσικής (1-152)

Τα κουίζ αυτά είναι επιλεγμένα από διάφορες πηγές, όπως το ίντερνετ, το περιοδικό "Περισκόπιο της Επιστήμης", το βιβλίο "Το κοτόπουλο από το Μινσκ" και την εμπειρία του γράφοντος.

Αφιερωμένα στον δάσκαλό μου Γεώργιο Στεφανίδη.

Πηγή εικόνων: public domain

Κάποια από τα κουίζ έχουν την απάντησή τους στις "Διευκρινίσεις Φυσικής" στο ίδιο blog: https://geometax12.blogspot.com/2018/07/blog-post_9.html

Καλημέρα, και καλωσήρθατε στα Θαύματα της Φυσικής.

1. Μέσα σ’ ένα κλειστό δωμάτιο βρίσκονται τρείς λάμπες, που ανάβουν από τρείς διακόπτες έξω από το δωμάτιο, χωρίς όμως να υπάρχει προφανής αντιστοιχία μεταξύ κάθε διακόπτη και λάμπας. Στην αρχή όλες οι λάμπες είναι σβηστές.

O παρατηρητής μπορεί να κάνει οποιοδήποτε χειρισμό των διακοπτών όσο είναι απ’ έξω, και μετά μπαίνοντας στο δωμάτιο θα πρέπει να βρει την αντιστοιχία κάθε διακόπτη με τη λάμπα του.

    ΑΠ. Ανάβει για λίγο έναν τυχαίο διακόπτη και μετά τον σβήνει, ανάβει έναν δεύτερο και τον αφήνει αναμμένο, και μετά μπαίνει στο δωμάτιο. Ο πρώτος διακόπτης ανάβει τη σβηστή αλλά ζεστή λάμπα, ο δεύτερος προφανώς αυτή που ανάβει, και ο τρίτος την σβηστή και κρύα λάμπα.

2. Αν οι αστροναύτες πάρουν μαζί τους σε τροχιά ένα καναρίνι, αυτό θα πεθάνει γρήγορα από δίψα. Γιατί?

    ΑΠ. Επειδή τα πουλιά για να καταπιούν χρειάζονται βαρύτητα, δεν έχουν μυς στο λαιμό για την προώθηση της τροφής.

3α. Από αεροπλάνο που πετάει σε ύψος 1966 m πάνω από το έδαφος πέφτει ένα εξάρτημα, που μετά από 20 s χτυπάει μια αρκούδα στο κεφάλι. Αν δεν λάβουμε υπόψη την αντίσταση του αέρα, να βρεθεί το χρώμα της αρκούδας.

3β. Αρκούδα πέφτει από βράχο ύψους 4.91 m και μετά από 1 s ακριβώς, χτυπάει στο έδαφος. Να βρεθεί το χρώμα της αρκούδας.

Δίνονται: g_πόλων = 9.83 m/s²,     g_ισημ. = 9.78 m/s²

(Η 3α και 3β είναι παραλλαγές ουσιαστικά της ίδιας άσκησης, που αποδίδεται στον καθηγητή Φυσικής του Πανεπιστημίου Αθηνών Καίσαρα Αλεξόπουλο (1909 – 2010). Σχετική είναι και η ερώτηση Νο 44).

    ΑΠ. Λευκή. Από τον τύπο της ελεύθερης πτώσης υπολογίζουμε το g και το συγκρίνουμε με τις τιμές που δίνονται.

4. Υπάρχει κάτι που μπορούμε να το μεταφέρουμε στη Σελήνη και εκεί να ζυγίζει περισσότερο απ’ ότι στη Γη?

    ΑΠ. Ένα μπαλόνι με ήλιο, με την προϋπόθεση ότι το υλικό του περιβλήματος είναι αρκετά ανθεκτικό για να αντέξει την διαφορά πίεσης με το κενό του περιβάλλοντος.

5. Αν ρουφώντας μπορούμε να μειώσουμε την ατμοσφαιρική πίεση κατά 50%, από ποιό μέγιστο ύψος (ως προς το ποτήρι) μπορούμε να ρουφήξουμε το ποτό μας με καλαμάκι?

    ΑΠ. Περίπου από τα 5 m, δεδομένου ότι η ατμοσφαιρική πίεση (στην επιφάνεια της θάλασσας) αντιστοιχεί σε υδάτινη στήλη 10 m.

6. Αν ένας φελλός βρίσκεται στον πάτο ενός κουβά με νερό, και τον ελευθερώσουμε την ίδια στιγμή που αφήνουμε τον κουβά να πέσει ελεύθερα, προς τα πού θα κινηθεί ο φελλός? (Στην εικόνα, φυσαλίδα αέρα μέσα σε νερό, σε μικροβαρύτητα).

    ΑΠ. Θα μείνει ακίνητος στον πάτο, γιατί κατά την ελεύθερη πτώση υγρού δεν ασκείται άνωση, καθώς εξαιτίας της έλλειψης συνισταμένων δυνάμεων το νερό δεν αναπτύσσει πίεση και κατά συνέπεια ούτε άνωση. Μάλιστα αν το νερό αφεθεί ελεύθερο σε μηδενική βαρύτητα (όπως μέσα σε διαστημόπλοιο σε τροχιά), τείνει να πάρει σφαιρικό σχήμα εξαιτίας της επιφανειακής τάσης του, και φυσαλίδες αέρα στο εσωτερικό του παραμένουν σχεδόν ακίνητες.

7. Ένας μεταλλικός σωλήνας που μέσα του γνωρίζουμε ότι ρέει νερό διαπερνά ένα δωμάτιο. Μέσα από το δωμάτιο και με απλά μέσα, πώς μπορούμε να διαπιστώσουμε τη φορά της ροής του νερού?

    ΑΠ. Θερμαίνουμε το μέσο περίπου του σωλήνα, και συγκρίνουμε τη θερμοκρασία του εκατέροθεν και σε ίσες αποστάσεις από το σημείο θέρμανσης. Το υγρό θα ρέει προς το θερμότερο σημείο.

8. Ένας παρουσιαστής μετεωρολογίας στην Καναδική TV, συνήθιζε να αναφέρει τις θερμοκρασίες περιβάλλοντος τόσο σε βαθμούς Κελσίου, όσο και σε Φαρενάιτ.

Μια μέρα, σε μια πρόβλεψη για έντονο κρύο, ανέφερε πτώση της θερμοκρασίας στους -40 βαθμούς, χωρίς άλλη διευκρίνιση. Ξέχασε κάτι?

    ΑΠ. Όχι, οι -40 βαθμοί Κελσίου συμπίπτουν με τους -40 βαθμούς Φαρενάιτ.

9. Σε ένα ποτήρι ξέχειλο με νερό επιπλέει ένα παγάκι. Όταν λιώσει το παγάκι, θα χυθεί κάποια ποσότητα νερού?

    ΑΠ. Όχι, ο όγκος του νερού που θα προκύψει από το λιωμένο παγάκι, θα ισούται με τον όγκο του βυθισμένου τμήματός του.

10. Ένας χωρικός ζητάει από έναν Μηχανικό, έναν Φυσικό και έναν Μαθηματικό να του περιφράξουν την μέγιστη δυνατή περιοχή, με ένα συγκεκριμένο τμήμα συρματοπλέγματος.

Ο Μηχανικός σχημάτισε έναν κύκλο, καθώς έχει τη μέγιστη επιφάνεια για δεδομένη περίμετρο.

Ο Φυσικός σχημάτισε μια ευθεία βορρά – νότο, και δήλωσε ότι επεκτείνει τις δύο ημιευθείες μέχρι να συναντηθούν, άρα κυκλώνει ένα ημισφαίριο.

Τι έκανε ο Μαθηματικός και τους ξεπέρασε όλους?

    ΑΠ. Δημιούργησε ένα κύκλο γύρο από τον εαυτό του με το συρματόπλεγμα, και δήλωσε ότι βρίσκεται ΕΞΩ από τον περιφραγμένο χώρο.

11. Ένας οπωροπώλης βγάζει στον ήλιο 200 κιλά αγγούρια, που περιέχουν 99% νερό. Στο τέλος της ημέρας δεν έχει πουλήσει κανένα, αλλά τώρα τα αγγούρια περιέχουν 98% νερό. Ποιο είναι τώρα το συνολικό τους βάρος?

    ΑΠ. 100 κιλά. Στην αρχή τα αγγούρια είχαν 1%, δηλαδή 2 κιλά, στερεά. Τα στερεά φυσικά παρέμεινα αμετάβλητα, άρα όταν στο τέλος 2 κιλά στερεών αποτελούν το 2%, το συνολικό βάρος είναι 100 κιλά.

12. Δύο κύλινδροι με τις ίδιες ακριβώς εξωτερικές διαστάσεις και βαμμένοι στο ίδιο χρώμα, έχουν ακριβώς το ίδιο βάρος.

Ο ένα όμως είναι χάλκινος και ο άλλος από αλουμίνιο, και προφανώς ο χάλκινος έχει τρύπα κατά τον άξονά του ώστε να έχει το ίδιο βάρος με τον αλουμινένιο, η οποία όμως έχει καλυφθεί εξωτερικά ώστε να μη διακρίνεται. Πώς μπορούμε να ξεχωρίσουμε ποιος κύλινδρος είναι ποιος? (Προσοχή! Η εικόνα αποκλίνει από την περιγραφή).

    ΑΠ. Τους αφήνουμε να κυλίσουν σε κεκλιμένο επίπεδο. Ο χάλκινος κύλινδρος, με τη μεγαλύτερη ροπή αδράνειας (αφού έχει τη μάζα του σε μεγαλύτερη μέση ακτίνα από τον αλουμινένιο κύλινδρο) θα καθυστερήσει. Για αντίστοιχο λόγο δεν μπορούμε να προσομοιώσουμε το πείραμα του Γαλιλαίου με την πτώση των διαφορετικών σφαιρών χρησιμοποιώντας κεκλιμένο επίπεδο, επειδή υπεισέρχεται η κύλιση και η διαφορετική ροπή αδράνειας των σφαιρών.

13. Δύο σφαίρες από συμπαγή σίδηρο αλλά με διαφορετικό μέγεθος, αφήνονται να πέσουν ελεύθερα από αρκετό ύψος σε πραγματικές συνθήκες (δηλαδή η αντίσταση του αέρα λαμβάνεται υπόψη). Ποια θα φτάσει πρώτη στο έδαφος? (Στην εικόνα, αναπαράσταση του πειράματος του Γαλιλαίου). 

    ΑΠ. Με μικρή διαφορά η μεγαλύτερη σφαίρα, επειδή όσο η διάμετρος μιας σφαίρας μεγαλώνει, ο λόγος της αδρανειακής μάζας της (που έχει σχέση με την 3^η δύναμη της ακτίνας της), ως προς τη μετωπική επιφάνειά της (που έχει σχέση με τη 2^η δύναμη της ακτίνας της), μεγαλώνει. Αυτό σημαίνει ότι στη μεγαλύτερη σφαίρα η αντίσταση του αέρα παίζει μικρότερο ρόλο σε σχέση με την αδρανειακή της μάζα, απ’ ότι στη μικρότερη σφαίρα.

14. Αν αφήσουμε ανοικτή την πόρτα ενός ψυγείου και το βάλουμε σε λειτουργία μια μέρα με πολύ ζέστη, ο χώρος (το δωμάτιο) τελικά θα δροσιστεί?

    ΑΠ. Όχι, μάλιστα θα θερμανθεί λιγάκι, εξαιτίας των απωλειών ενέργειας του ηλεκτρικού συμπιεστή του ψυγείου. Το ψυγείο όπως και τα κλιματιστικά, είναι αντλίες θερμότητας που μεταφέρουν θερμότητα από την μία συσκευή (του σετ που αποτελούνται) στην άλλη. Στο ψυγείο όμως και οι δύο συσκευές βρίσκονται επάνω του (η ψυχρή μέσα και η θερμή έξω, στο μαύρο μεταλλικό πλέγμα στο πίσω μέρος του).

15. Στο μέσο περίπου του θαλάμου ενός λεωφορείου κρεμάμε από το ταβάνι ένα μπαλόνι με ατμοσφαιρικό αέρα, και από το πάτωμα ένα μπαλόνι με ήλιο. Κατά την επιτάχυνση του λεωφορείου, προς τα που θα κινηθούν τα μπαλόνια και γιατί? (Στην εικόνα φαίνεται μόνο το μπαλόνι με το ήλιο).

    ΑΠ. Το μπαλόνι με τον αέρα θα κινηθεί προς τα πίσω (μαζί με την κίνηση του υπόλοιπου αέρα εξαιτίας της αδράνειάς του), αλλά το μπαλόνι με το ήλιο προς τα εμπρός, καθώς εκτοπίζεται από τη συσσώρευση της μάζας του αέρα (και την αύξηση της πυκνότητάς του) προς το πίσω μέρος του λεωφορείου.

16. Σε μια υποθετική συμπαγή σφαίρα στο μέγεθος της Γης, τυλίγουμε γύρω από τον ισημερινό της ένα καλώδιο. Αν θελήσουμε, αντί το καλώδιο να βρίσκεται στο έδαφος να το στερεώσουμε σε πασσάλους σε ύψος 1 m, πόσο μεγαλύτερο μήκος καλωδίου θα χρειαστεί?

    ΑΠ. Περίπου 6 m. Το αρχικό μήκος του καλωδίου είναι 2πR, ενώ μετά τη στερέωσή του στους πασσάλους θα είναι 2π(R+1m) = 2πR + 2π m, η διαφορά λοιπόν είναι μόνο 2π m = 6.28 m. Το ενδιαφέρον είναι, ότι το μήκος αυτό είναι ανεξάρτητο από το μέγεθος της σφαίρας - πλανήτη.

17. Ζυγίζουμε ένα ποτήρι τελείως γεμάτο με νερό. Στη συνέχεια τοποθετούμε με προσοχή ένα αντικείμενο που δεν βυθίζεται τελείως, και απομακρύνουμε το νερό που ξεχείλισε, πριν ξαναζυγίσουμε το ποτήρι. Πώς θα έχει μεταβληθεί τώρα το βάρος του ποτηριού, σε σχέση με την προηγούμενη ζύγιση?

    ΑΠ. Δεν θα μεταβληθεί, επειδή το βάρος του νερού που ξεχείλισε ισούται με το βάρος του αντικειμένου που προστέθηκε (εφόσον επιπλέει). Αυτή η αρχή μάλιστα έχει χρησιμοποιηθεί στον Τροχό του Falkirk στην Σκωτία (κατακόρυφη μεταφορά σκαφών σε κανάλια), για εξοικονόμηση ενέργειας (βλ και ερώτηση Νο 24).

18. Σε μία βάρκα έχει τοποθετηθεί στο κατάρτι της ένα τετράγωνο πανί, έτσι ώστε η επιφάνειά του να είναι εγκάρσια στη βάρκα. Στην πρύμνη της βάρκας έχει τοποθετηθεί ένας ανεμιστήρας με μπαταρία, έτσι ώστε να φυσάει προς το πανί.

Αν ενεργοποιήσουμε τον ανεμιστήρα μια μέρα χωρίς καθόλου αέρα, προς τα πού θα κινηθεί η βάρκα?

    ΑΠ. Προς τα εμπρός, αν και με μικρή ταχύτητα, επειδή παρόλο που το σύστημα φαίνεται κλειστό, η ροή του αέρα που θα χτυπήσει στο πανί θα έχει μικρότερη ταχύτητα αλλά μεγαλύτερη διάμετρο από τη ροή στον ανεμιστήρα, άρα καλύτερη απόδοση μεταφοράς ορμής.

19. Μπορεί ζεστό νερό να χρησιμοποιηθεί για ψύξη?

    ΑΠ. Φυσικά, αρκεί η επιφάνεια προς ψύξη να είναι θερμότερη από το νερό.

20. Γιατί όταν φυσάει κρυώνουμε περισσότερο, και όταν έχει υγρασία ζεσταινόμαστε περισσότερο?

    ΑΠ. Γιατί η ροή του αέρα έχει διπλό ψυκτικό αποτέλεσμα στο ανθρώπινο δέρμα. Απομακρύνει το ακίνητο στρώμα του αέρα που μονώνει το δέρμα από το περιβάλλον (ακόμα και μέσα από τα ρούχα), και προκαλεί εξάτμιση της υγρασίας που πάντα υπάρχει στο ανθρώπινο δέρμα. Από την άλλη μεριά, η εξάτμιση της υγρασίας του δέρματος εμποδίζεται εάν υπάρχει ήδη αυξημένη υγρασία στην ατμόσφαιρα μια ζεστή μέρα, οπότε ο άνθρωπος χάνει σε μεγάλο βαθμό το ψυκτικό αποτέλεσμα της εξάτμισης αυτής.

Στο ίντερνετ δημοσιεύονται πίνακες που δείχνουν τόσο την επίδραση του ανέμου όσο και της υγρασίας, στην αίσθηση κρύου και ζέστης αντίστοιχα που έχει ο άνθρωπος. 

21. Αν ο «Μικρός Πρίγκιπας» χοροπηδάει στον μικροσκοπικό πλανήτη του, θα του αλλάξει τροχιά?

     ΑΠ. Όχι, γιατί πρόκειται για κλειστό σύστημα από πλευράς ορμής. Θα αναρωτηθεί κανείς βέβαια, ότι αφού ο ΜΠ σπρώχνει το έδαφος με τα πόδια του, τόσο όταν πηδάει όσο και όταν προσγειώνεται, πώς γίνεται να μην επηρεάζει την τροχιά του. Γίνεται όμως, επειδή όσο βρίσκεται στον αέρα έλκεται αμοιβαία με τον πλανήτη του, και «επαναφέρει» τον πλανήτη στην τροχιά του και τον εαυτό του στην επιφάνειά του. 

 

22. Στο πείραμα για να ανέβει το νερό από μία λεκάνη όσο ψηλότερα γίνεται, ρουφώντας μέσα από έναν μακρύ σωλήνα, κάποιος προτείνει να χρησιμοποιήσουν στο επάνω μέρος τού σωλήνα μια διάταξη σχήματος «Τ» με δύο στόμια, ώστε να μπορούν να ρουφήξουν ταυτόχρονα δύο άτομα, διπλασιάζοντας έτσι την υποπίεση μέσα στον σωλήνα. Έχει δίκιο?

    ΑΠ. Όχι, και αυτό γίνεται εύκολα κατανοητό αν θεωρήσουμε ότι στο ένα οριζόντιο στόμιο του «Τ» υπάρχει μια χειροκίνητη βαλβίδα. Με τη βαλβίδα κλειστή, και χρησιμοποιώντας φυσικά το άλλο στόμιο, το πρώτο άτομο ρουφάει όσο μπορεί και ας υποθέσουμε ότι κατεβάζει την πίεση μέσα στο σωλήνα στη μισή της ατμοσφαιρικής. Τώρα το δεύτερο άτομο ρουφάει και αυτό από το κλειστό (με τη βαλβίδα) στόμιο και κατεβάζει την πίεση και σε αυτό το τμήμα, δηλαδή μέχρι τη βαλβίδα, στη μισή ατμόσφαιρα. Αν ανοίξει τώρα η βαλβίδα, τίποτα δεν πρόκειται να αλλάξει από πλευράς πίεσης, θα συνεχίζει δηλαδή να επικρατεί πίεση μισής ατμόσφαιρας μέσα στον σωλήνα.
 

23. Ένας ιθαγενής στην Αφρική κυνηγάει στη σαβάνα με το τόξο του, όταν σε κάποια απόσταση εντοπίζει έναν πίθηκο (του είδους nostimus nostimus), να κρέμεται με το ένα χέρι του από τα κάτω κλαδιά ενός δέντρου, σε ύψος 4 m από το έδαφος.

Ο ιθαγενής, επειδή ο πίθηκος κοιτάζει προς το μέρος του τεντώνει αργά το τόξο του, γνωρίζοντας όμως ότι μόλις το βέλος εκτοξευθεί, ο πίθηκος θα το αντιληφθεί και θα αφήσει το κλαδί.

Από την εμπειρία του γνωρίζει επίσης, ότι από αυτή την απόσταση θα πρέπει να σημαδέψει 2 m ψηλότερα από έναν στόχο που παραμένει ακίνητος, για να αντισταθμίσει την απώλεια ύψους του βέλους του.

Πώς θα πρέπει να σημαδέψει όμως σ’ αυτή την περίπτωση?

    ΑΠ. Θα πρέπει να σημαδέψει ΕΠΑΝΩ στον πίθηκο, επειδή το βέλος  και ο πίθηκος θα πέφτουν με την ίδια ταχύτητα προς το έδαφος, οπότε μοιραία (για τον πίθηκο) θα συναντηθούν.

24. Στο Falkirk, στη Σκωτία, υπάρχει ένα σύστημα που μεταφέρει κατακόρυφα σκάφη μεταξύ δύο καναλιών, που εξαιτίας της διαμόρφωσης του εδάφους βρίσκονται σε αρκετά διαφορετικό υψόμετρο.

Το σύστημα λειτουργεί σαν ζυγός, με δύο όμοιες δεξαμενές στα άκρα του, που διατηρούνται οριζόντιες και γεμάτες νερό στην ίδια στάθμη (εικόνα κάτω).

Όταν το σύστημα λειτουργεί, η μία δεξαμενή ανεβαίνει στο ύψος του επάνω καναλιού και η άλλη χαμηλώνει στο επίπεδο του όμοιου κάτω καναλιού, οι υδατοφράκτες ανοίγουν και ένα σκάφος μπαίνει στη μία δεξαμενή και αν υπάρχει (για την αντίστροφη διαδρομή), ένα δεύτερο σκάφος μπαίνει στην άλλη.

Ο ζυγός κινείται, οι δεξαμενές αλλάζουν επίπεδο, οι υδατοφράχτες ανοίγουν και τα σκάφη βγαίνουν και συνεχίζουν το ταξίδι τους έχοντας αλλάξει κανάλι.

Πώς όμως το ευφυές αυτό σύστημα κατορθώνει να έχει ελάχιστη κατανάλωση ενέργειας κατά τη λειτουργία του, και μάλιστα ανεξάρτητα από την παρουσία ή όχι σκάφους σε κάθε δεξαμενή, αλλά και από το μέγεθος του σκάφους?

    ΑΠ. Αξιοποιεί την αρχή του Αρχιμήδη, σύμφωνα με την οποία, κάθε σκάφος εκτοπίζει νερό ίσο με το βάρος του. Αφού λοιπόν η στάθμη του νερού σε κάθε δεξαμενή διατηρείται σταθερή, καθώς επικοινωνεί με κανάλι ίδιας στάθμης κατά τη διαδικασία φόρτωσης – εκφόρτωσης των σκαφών, το συνολικό ωφέλιμο βάρος (νερό + σκάφος) παραμένει σταθερό και ο ζυγός είναι πάντα «ζυγισμένος»! 

25. Ένας μηχανικός επιθεωρεί μια γραμμή ηλεκτροδότησης 1000V στην Αφρική, όταν διαπιστώνει ότι ένας εξαγριωμένος γορίλας τον καταδιώκει.

Προσπαθώντας να ξεφύγει, ο μηχανικός σκαρφαλώνει στον κοντινότερο πυλώνα της γραμμής ηλεκτροδότησης, και όταν διαπιστώνει ότι ο γορίλας τον ακολουθεί πάνω στον πυλώνα, συσπειρώνεται και κάνοντας την μεγαλύτερη εκτίναξη της ζωής του, αρπάζεται από τον πλησιέστερο αγωγό και βρίσκεται έτσι να αιωρείται πάνω από το έδαφος.

Ο γορίλας προσπαθώντας να τον φτάσει, όπως είναι ανεβασμένος στον πυλώνα απλώνει το χέρι του για να πιάσει τον αγωγό, αλλά δέχεται μια ισχυρή ηλεκτρική εκκένωση και πέφτει τρομαγμένος και καψαλισμένος στο έδαφος.

Τι έκανε λάθος ο γορίλας?

    ΑΠ. Προφανώς ο γορίλας δεν έδωσε σημασία στο ότι ο μηχανικός πήδηξε στον αέρα για να πιαστεί από τον αγωγό, με τρόπο ώστε να μην αγγίζει ταυτόχρονα τον πυλώνα και τον αγωγό. Πιάνοντας τον αγωγό ενώ βρίσκονταν ακόμα επάνω στον πυλώνα, ο γορίλας δέχτηκε την εκκένωση της τάσης του αγωγού προς την κολώνα και το έδαφος, μέσα από το σώμα του.

Βέβαια ο μηχανικός δεν θα μπορούσε να κάνει το ίδιο αν η γραμμή ηλεκτροδότησης ήταν Υψηλής Τάσης, καθώς για να έλθουν σε επαφή με αυτή ενώ βρίσκεται σε λειτουργία, οι τεχνίτες εργάζονται από ελικόπτερο και φορούν ειδική ολόσωμη στολή με κουκούλα γάντια κλπ, που έχει ενσωματωμένο ένα πλέγμα από συρματίδια αργύρου. Με αυτό τον τρόπο δημιουργείται ένα «κλωβός Φαραντέι» για το ηλεκτρικό πεδίο, που στην Υψηλή Τάση είναι αρκετά ισχυρό ώστε να προκαλέσει ροή ρεύματος μέσα στο σώμα, επικίνδυνη για έναν απροστάτευτο άνθρωπο. 

Εξάλλου ο μηχανικός βρέθηκε σε μία κατάσταση "ζωής ή θανάτου".

26. Τί θα συμβεί στο βάρος μιας ποσότητας σιδηρόμαλλου (μπαλάκι από πολύ λεπτό σύρμα σαν αυτό με το οποίο καθαρίζουμε μεταλλικά σκεύη) αν το κάψουμε με φλόγιστρο?

    ΑΠ. Το βάρος του σιδηρόμαλλου, αντίθετα απ’ ότι συνήθως θα περιμέναμε, θα αυξηθεί (λιγάκι), επειδή η πυράκτωσή του το κάνει να οξειδώνεται, και καθώς το μόριο του σίδηρου ενώνεται με το οξυγόνο, «βαραίνει».

Το ίδιο θα διαπιστώσουμε αν ανάψουμε ένα από τα παλιού τύπου φωτογραφικά φλας με μαγνήσιο, και το ζυγίσουμε προσεκτικά πριν και μετά. Το αποτέλεσμα φαίνεται περίεργο, επειδή συνήθως συνδέουμε την καύση με την ένωση υλικών που περιέχουν άνθρακα η υδρογόνο, με οξυγόνο, οπότε σε αυτές τις περιπτώσεις παράγεται αέριο (ή υδρατμός) και πράγματι το αρχικό βάρος μειώνεται.

Ενδιαφέρον έχει επίσης ότι η καύση αυτοσυνηρείται, καθώς το σιδηρόμαλλο έχει πολύ μεγάλη επιφάνεια σε σχέση με τον όγκο του, οπότε η οξείδωσή του παράγει αρκετή θερμότητα για την πυράκτωσή του.

27. Ένας ιθαγενής που κυνηγάει ψάρια με βέλη στο ποτάμι, στέκεται πάνω σ’ ένα βράχο και προτιμάει να στοχεύει τα ψάρια που κινούνται ακριβώς από κάτω του, και όχι αυτά που βρίσκονται λίγο μακρύτερα, παρότι στη δεύτερη περίπτωση θα είχε μια πιο άνετη στάση τοξοβολίας. Γιατί? 

    ΑΠ. Γιατί η εικόνα των ψαριών που τα βλέπει κάθετα προς το νερό δεν υφίσταται μετατόπιση εξαιτίας της διάθλασης, οπότε η στόχευσή του είναι ακριβέστερη.

 28. Κάποιος που στέκεται στη μέση του δρόμου, πετάει στο παρμπρίζ ενός λεωφορείου που κινείται προς αυτόν με 40 km/h, ένα ελαστικό μπαλάκι. Εάν η ρίψη έγινε με ταχύτητα 20 km/h, με πόση ταχύτητα το μπαλάκι αφού αναπηδήσει στο παρμπρίζ, θα κινηθεί προς το μέρος του?

    ΑΠ. Με 100 km/h. Η ταχύτητα που θα έχει το μπαλάκι (ως προς το έδαφος) μετά την ανάκρουση, προκύπτει από τον τύπο: 2 Χ 40 + 20 = 100 km/h. Αυτό μπορούμε να το καταλάβουμε απλά, ως εξής: Ας φανταστούμε για μια στιγμή το μπαλάκι ακίνητο στον αέρα, με το λεωφορείο να το κτυπάει με 40 km/h. Αφού το μπαλάκι θα προσκρούσει ελαστικά στο παρμπρίζ, η αναπήδησή του θα γίνει με την ίδια ταχύτητα (κατά μέτρο) με την ταχύτητα πρόσκρουσης, άρα ο οδηγός θα δει το μπαλάκι θα απομακρύνεται από το παρμπρίζ του με 40 km/h. Όμως, η ταχύτητα του λεωφορείου θα πρέπει να προστεθεί και αυτή στην ταχύτητα ανάκρουσης, οπότε έχουμε συνολικά 2 Χ 40 = 80 km/h, για το αρχικά «αιωρούμενο» μπαλάκι. Στο κινούμενο μπαλάκι όμως θα πρέπει να προσθέσουμε και την αρχική ταχύτητά του, η οποία φυσικά δεν αλλοιώνεται (κατά μέτρο) αφού η πρόσκρουση είναι ελαστική απλά αντιστρέφει τη φορά της, οπότε η τελική ταχύτητα είναι 2 Χ 40 + 20 = 100 km/h. 

29. Τι θα παρατηρήσουμε αν συνδέσουμε μέσα από έναν κοντό σωλήνα τα στόμια δύο μπαλονιών που είναι περίπου το ίδιο φουσκωμένα?

    ΑΠ. Ότι το ένα μπαλόνι, και μάλιστα αυτό που είναι λιγότερο φουσκωμένο, θα ξεφουσκώσει ακόμα περισσότερο, μεταφέροντας τον αέρα του στο άλλο μπαλόνι που με τη σειρά του θα φουσκώσει περισσότερο. Αυτό οφείλεται στο ότι η πίεση στο εσωτερικό ενός μπαλονιού είναι τόσο μεγαλύτερη όσο μικρότερη είναι η διάμετρός του, και αυτό συμβαίνει γενικά με όλες τις «φουσκάλες». Το παραπάνω ισχύει  εφόσον το μπαλόνι είναι αρκετά μαλακό και δεν βρίσκεται στα δύο άκρα της τάνυσής του, δηλαδή πολύ λίγο ή πάρα πολύ φουσκωμένο. Η εξήγηση του φαινομένου έχει να κάνει με τη συνισταμένη των δυνάμεων που τεντώνουν τα τοιχώματα του μπαλονιού. Αν φανταστούμε ένα μικρό τόξο, μήκους πχ 1 cm επάνω σε μια τομή της επιφάνειας του μπαλονιού, τότε η συνισταμένη των δυνάμεων στα άκρα του (που είναι εφαπτομενικές στην καμπυλότητα του μπαλονιού) θα είναι μεγαλύτερη όσο μικρότερη είναι η διάμετρος του μπαλονιού. Και το γεγονός ότι η συνισταμένη αυτή είναι αντίθετη στη δύναμη που προκύπτει από την πίεση που υπάρχει μέσα στο μπαλόνι, σημαίνει ότι και η πίεση θα είναι μεγαλύτερη σε μπαλόνι μικρότερης διαμέτρου.

30. Αυτή είναι μια πραγματική ιστορία.

Ο Αbraham Wald ήταν Αμερικανός στατιστικολόγος κατά τον Β’ ΠΠ, στον οποίον ανατέθηκε να καταγράψει τις ζημιές σε βομβαρδιστικά που επέστρεφαν από πολεμικές αποστολές, έτσι ώστε στη συνέχεια να προτείνει βελτιώσεις για την προστασία των αεροσκαφών.

Ο Wald βρήκε ότι οι περισσότερες ζημιές στα αεροσκάφη που επέστρεφαν ήταν στην άτρακτο και το σύστημα καυσίμων, αλλά η πρόταση που έκανε για τα ποια τμήματα χρειάζονταν περισσότερη προστασία, αποτέλεσε τεράστια έκπληξη για τους ανωτέρους του. Τι πρότεινε?

    ΑΠ. Πρότεινε να προστατευτούν τα τμήματα των αεροπλάνων που ΔΕΝ εμφάνιζαν ζημιές κατά την επιστροφή τους. Η λογική ήταν ότι τα πιο ευπαθή τμήματα ήταν αυτά ακριβώς που δεν εμφάνιζαν ζημιές, διότι προφανώς αν κάποιο αεροσκάφος ΕΙΧΕ ζημιές στα τμήματα αυτά, δεν κατόρθωνε ποτέ να επιστρέψει ώστε οι ζημιές αυτές να καταγραφούν! Αυτό έγινε γνωστό σαν "μεροληψία επιβίωσης" (survivorship bias).

31. Το παρακάτω είναι γνωστό σαν το παράδοξο του Monty, από το όνομα του Αμερικανού παρουσιαστή που το χρησιμοποιούσε σε διαγωνισμό. Και παρόλο που είναι ένα κουίζ στατιστικής, περιλαμβάνεται εδώ εξαιτίας του ενδιαφέροντός του.

Ο παρουσιαστής ζητούσε από τον διαγωνιζόμενο να διαλέξει μία από τρείς κλειστές πόρτες που του παρουσίαζε, πίσω από την οποία κρύβονταν ένα δώρο, ενώ στις άλλες δύο δεν υπήρχε τίποτα. Αφού ο διαγωνιζόμενος ανακοίνωνε την επιλογή του, ο Monty άνοιγε μια από τις ΑΛΛΕΣ δύο πόρτες, που ο ίδιος γνώριζε εκ των προτέρων ότι από πίσω της δεν υπήρχε τίποτα. Στη συνέχεια ζητούσε από τον διαγωνιζόμενο να επιλέξει αν θα παρέμενε με την αρχική επιλογή του, ή αν ήθελε θα μπορούσε να την αλλάξει, επιλέγοντας την τρίτη πόρτα που δεν είχε ανοίξει. Τι ήταν έξυπνο να κάνει ο διαγωνιζόμενος?

    ΑΠ. Να αλλάξει την επιλογή του καθώς έτσι θα είχε διπλάσιες πιθανότητες να κερδίσει, παρά αν έμενε με την πρώτη επιλογή του. Ας θεωρήσουμε ότι οι πόρτες είναι η Α, Β και Γ, και ότι η πρώτη επιλογή του διαγωνιζόμενου είναι η Α.

Η πιθανότητα να είναι το δώρο πίσω της είναι 1/3, ενώ η πιθανότητα να είναι πίσω από την Β ή την Γ είναι συνολικά 2/3. Όταν ο παρουσιαστής αποκαλύπτει την πόρτα (μεταξύ της Β και Γ) που δεν έχει το δώρο, ας πούμε την Β, η πιθανότητα να βρίσκεται το δώρο στο «πακέτο» Β ή Γ, παραμένει 2/3, αλλά τώρα δεδομένου ότι έγινε γνωστό ότι η Β δεν έχει δώρο, το σύνολο των αρχικών πιθανοτήτων 2/3 του «πακέτου», αφορά πλέον μόνο την πόρτα Γ.

Συνεπώς, η επιλογή της Γ διπλασιάζει τις πιθανότητες του διαγωνιζόμενου να κερδίσει, παρά αν παρέμενε με την αρχική επιλογή της πόρτας Α, που είναι 1/3.

Το παράδοξο γίνεται επίσης κατανοητό αν σκεφτούμε ότι η αποκάλυψη από τον Monty της πόρτας που δεν έχει δώρο, είναι αυτή η οποία αυξάνει τις πιθανότητες του διαγωνιζόμενου, εφόσον αλλάξει την επιλογή του. 

32. Τι πλεονέκτημα έχουν τα στρογγυλά καλύμματα φρεατίων έναντι των τετράγωνων / ορθογώνιων?

    ΑΠ. Αν λάβουμε υπόψη και την πατούρα που αναγκαστικά έχει η τρύπα, θα δούμε ότι ένα στρογγυλό καπάκι ΔΕΝ ΧΩΡΑΕΙ με κανέναν τρόπο για να πέσει στον υπόνομο, ενώ αυτό αυτό δεν ισχύει για τα τετράγωνα / ορθογώνια. 

33. Ένας εξερευνητής βρίσκεται στο κέντρο ενός οροπεδίου, που έχει τρείς πολύ απότομες πλευρές και ψηλό ξερό χορτάρι, όταν στην μόνη πλευρά του οροπεδίου που υπάρχει διέξοδος ξεσπά πυρκαγιά, και μάλιστα ο αέρας την κάνει να κινείται προς το μέρος του. Πώς μπορεί να διαφύγει?

    ΑΠ. Βάζει φωτιά στη μέση περίπου του οροπεδίου, και την ακολουθεί καθώς η φωτιά προχωράει προς την απόκρημνη άκρη του. Όταν η αρχική φωτιά φτάσει στη μέση του οροπεδίου θα σβύσει από έλλειψη καυσίμου, και αυτός θα μπορέσει να διαφύγει.

34. Βλέπουμε το είδωλό μας σ’ έναν μεγάλο ολόσωμο καθρέφτη, και κινούμαστε προς το μέρος του με 3 km/h. Με ποια ταχύτητα συγκλίνουμε με το είδωλό μας?

    ΑΠ. Mε τη διπλάσια ταχύτητα δηλαδή 6 km/h, επειδή το είδωλό μας κινείται και αυτό με την ίδια ταχύτητα με εμάς προς την επιφάνεια του καθρέφτη.

35. Βλέπουμε πράγματι τον εαυτό μας μέσα στον καθρέφτη?

    ΑΠ. Όχι, στην πραγματικότητα βλέπουμε κάποιον που του μοιάζει καταπληκτικά, επειδή στο είδωλο του καθρέφτη η δεξιά με την αριστερή πλευρά αντιστρέφονται. Συνεπώς μόνο αν έχουμε ένα απόλυτα συμμετρικό πρόσωπο (πράγμα πολύ σπάνιο), θα δούμε τον εαυτό μας στον καθρέφτη όπως τον βλέπουν οι άλλοι.  Αλλιώς, θα πρέπει να κοιτάξουμε απλά... μια φωτογραφία μας. Όμως, το είδωλο στον καθρέφτη δεν αντιστρέφει και το επάνω με το κάτω, καθώς αντανακλά κάθε περιοχή προς την ίδια πλευρά. Κάτι ανάλογο διαπιστώνουν και όσοι πετούν τηλεκατευθυνόμενο αεροπλανάκι. Όταν έρχεται προς το μέρος τους, η φορά του χειριστηρίου για τη δεξιά ή αριστερή κλίση αντιστρέφεται, όχι όμως και του χειριστηρίου για την άνοδο / κάθοδο.

36. Έχουμε δύο ελαστικά μπαλάκια ίσου ή διαφορετικού μεγέθους. Αν τα αφήσουμε να πέσουν ελεύθερα (χωρίς αρχική ταχύτητα) από συγκεκριμένο ύψος, μπορούμε να κάνουμε το ένα τουλάχιστον να αναπηδήσει αρκετά περισσότερο από το αρχικό ύψος?

    ΑΠ. Ναι, αν τοποθετήσουμε το ένα (το μικρότερο αν είναι άνισα) ακριβώς επάνω από το άλλο, έτσι ώστε απλά να το ακουμπάει, και τα αφήσουμε να πέσουν ταυτόχρονα. Θα παρατηρήσουμε ότι το επάνω μπαλάκι θα αναπηδήσει αρκετά παραπάνω από το αρχικό ύψος, ενώ αντίθετα το κάτω μπαλάκι θα αναπηδήσει πολύ λίγο. Αυτό συμβαίνει επειδή στην αναπήδηση της επάνω μπάλας συμβάλλει και η ενέργεια της κάτω μπάλας (μέσω της ελαστικής της παραμόρφωσής της), γι’ αυτό και η κάτω αναπηδάει πολύ λιγότερο. 

37. Ένας μαθητής αναμιγνύει για ένα πείραμα 50 ml νερού με 50 ml οινοπνεύματος. Με έκπληξή του παρατηρεί ότι μετά την ανάμιξη ο συνολικός όγκος του μίγματος είναι 94 ml. Είναι η έκπληξή του δικαιολογημένη? 

    ΑΠ. Όχι, γιατί θα έπρεπε να ξέρει ότι με την ανάμιξη οι όγκοι δεν προστίθενται ακριβώς, επειδή κάποια μόρια του ενός υγρού μπορούν να τοποθετηθούν ανάμεσα στα μόρια του άλλου υγρού. Μόνον οι μάζες προστίθενται, επειδή προφανώς η μάζα δεν χάνεται. 

38. Σε περιοχές που υπάρχουν οπωροφόρα δένδρα και σε περιόδους που η θερμοκρασία πέφτει κοντά στους 0 C, χρησιμοποιούνται «κανόνια» που ψεκάζουν νερό στα δέντρα. Γιατί? 

    ΑΠ. Επειδή η παγοποίηση του νερού επάνω στα φρούτα απελευθερώνει θερμότητα (τη λανθάνουσα θερμότητα πήξης του νερού, περίπου 80 cal/gr), που προστατεύει το εσωτερικό των φρούτων από το πάγωμα. 

39. Γιατί οι μηχανές των αυτοκινήτων μοιάζουν να χάνουν (ανεπαίσθητα βέβαια) ισχύ, σε ημέρες με πολύ υψηλή υγρασία? 

    ΑΠ. Επειδή η υγρασία καταλαμβάνει μέρος του όγκου του αέρα, και μειώνει το περιεχόμενο οξυγόνο. Για παράδειγμα, σε 1 m3 αέρα υγρασίας 50% και στους 23 C, περιέχονται 10 g νερού, ενώ αν η υγρασία ανέβει στο 100 % θα περιέχονται 20 g νερού. Καθώς η υγρασία είναι νερό σε αέρια μορφή, 18 g της καταλαμβάνουν όγκο 22.4 l, οπότε τα 10 επιπλέον g νερού της πολύ υγρής ημέρας στερούν από το 1 m3 αέρα 12.5 l, και το αντίστοιχο οξυγόνο τους. 

 

40. Αν δημιουργήσουμε ένα εκκρεμές που έχει σαν βαρίδι ένα ελαφρύ δοχείο που περιέχει νερό (όχι τελείως γεμάτο) και στη συνέχεια το νερό παγώσει, τι θα συμβεί με τη συχνότητα ταλάντωσης του εκκρεμούς?

    ΑΠ. Θα αυξηθεί, σαν αποτέλεσμα της ανόδου του κέντρου βάρους του νερού, εξαιτίας της αναγκαστικής διαστολής του προς τα επάνω με το πάγωμα.

 

41. Κατά τον Β’ΠΠ για την προστασία της ουράς των συμμαχικών βομβαρδιστικών από τις επιθέσεις των αεριωθούμενων γερμανικών καταδιωκτικών, δοκιμάστηκαν πύραυλοι χωρίς καθοδήγηση που εκτοξεύονταν από τα βομβαρδιστικά προς τα πίσω.
Γρήγορα όμως διαπιστώθηκε ότι οι πύραυλοι αυτοί κατέρριπταν τα ίδια τα βομβαρδιστικά από τα οποία εκτοξεύονταν! Τι συνέβαινε? 

    ΑΠ. Με την εκτόξευση του πυραύλου προς τα πίσω και μέχρι να επιταχυνθεί αρκετά ώστε η ταχύτητά του να γίνει τουλάχιστον ίση (κατά μέτρο) με την ταχύτητα του βομβαρδιστικού, ο πύραυλος βρίσκονταν να πετάει ανάποδα. Οπότε, όπως ένα βέλος που ρίχνεται ανάποδα, περιστρέφονταν αμέσως κατά 180 μοίρες, κατευθυνόμενος πλέον προς το ίδιο το βομβαρδιστικό! 

42. Ένας ρωμαϊκός ζυγός ισορροπεί με ένα ποτήρι με νερό (όχι γεμάτο) στη μία πλευρά του. Αν βυθίσουμε μέσα στο νερό το δάκτυλό μας χωρίς να αγγίξουμε τα τοιχώματα ή τον πάτο του ποτηριού, θα διαταραχθεί η ισορροπία του ζυγού? 

    ΑΠ. Ναι, η πλευρά του ποτηριού θα κατέβει, καθώς τώρα θα έχει προστεθεί στην πλευρά αυτή και η αντίδραση της άνωσης που ασκεί το νερό στο δάκτυλο (εικόνα κάτω).

43. Σε ποια περίπτωση ένας αστροναύτης δεν θα είχε πρόβλημα να υποστεί επιτάχυνση πολύ μεγάλης τιμής? 

    ΑΠ. Αν η επιτάχυνσή του οφείλεται σε ομοιογενές βαρυτικό πεδίο, επειδή όλα του τα μόρια θα επιταχύνονται ταυτόχρονα. Θα νοιώθει μάλιστα αβαρής, σαν να βρίσκεται σε ελεύθερη πτώση.

44. Μια αρκούδα περπατά νότια 3 χιλιόμετρα, μετά δυτικά 5 χιλιόμετρα, στη συνέχεια πάλι βόρεια 3 χιλιόμετρα, και τότε βρίσκεται πάλι στο σημείο που ξεκίνησε. Να βρεθεί το χρώμα της αρκούδας.

    ΑΠ. Λευκό, επειδή μόνο αν έχει αφετηρία τον βόρειο πόλο μπορεί να συμβεί αυτό.

45. Μπορείτε να σκεφτείτε μια περίπτωση που βαρυτική έλξη μεταξύ δύο στερεών σωμάτων μειώνεται, καθώς τα δύο σώματα πλησιάζουν μεταξύ τους?

    ΑΠ. Αυτό μπορεί να συμβεί πχ αν το ένα σώμα είναι δακτύλιος και το δεύτερο μια αρκετά μικρότερη σφαίρα.

Όταν τα σώματα είναι αρκετά μακριά, ισχύει μεταξύ των δύο μαζών ο παγκόσμιος νόμος της έλξης.

 Καθώς όμως η σφαίρα πλησιάζει αρκετά τον δακτύλιο κινούμενη επάνω στον κάθετο άξονά του, οι δυνάμεις της έλξης τείνουν να αλληλοεξουδετερωθούν εξαιτίας της συμμετρίας των ακτινικών συνιστωσών τους, με αποτέλεσμα όταν η σφαίρα βρεθεί στο κέντρο του δακτυλίου η συνισταμένη των ελκτικών δυνάμεων να είναι μηδέν.

Φυσικά αυτό είναι μία ασταθής ισορροπία που δεν μπορεί να διατηρηθεί στην πράξη, εκτός αν η σφαίρα ολισθαίνει επάνω σ’ έναν «οδηγό».
 

 46. Παίρνουμε μια ίσια και λεία βέργα (ή έναν μεγάλο χάρακα ή έναν ελαφρύ σωλήνα) μήκους περίπου 0.5m. Κρατάμε τις παλάμες μας κάθετες με τα χέρια λυγισμένα, όπως όταν πάμε να κάνουμε χειραψία. Τοποθετούμε τη βέργα επάνω στους δείκτες των χεριών μας, κοντά στα άκρα της.

Αν τώρα πλησιάσουμε τα χέρια μεταξύ τους (εικόνα), θα παρατηρήσουμε ότι ολισθαίνουν κάτω από τη ράβδο περίπου ομοιόμορφα, και συναντιόνται κοντά στο κέντρο της. Αν όμως απομακρύνουμε στη συνέχεια τα χέρια μας προς τα έξω, θα δούμε ότι η ράβδος ολισθαίνει πάνω από τη μία μόνο παλάμη, μέχρι να φτάσει στην άκρη.

Γιατί συμβαίνει αυτό?

    ΑΠ. Είναι θέμα τριβής, η οποία πέρα από το συντελεστή τριβής εξαρτάται και από το βάρος στο σημείο επαφής. Έτσι, καθώς οι παλάμες πλησιάζουν μεταξύ τους, αν η μία προηγηθεί, πέφτει επάνω της μεγαλύτερο μέρος του βάρους της ράβδου, η τριβή αυξάνεται και τότε ολισθαίνει η άλλη πλευρά.

Αυτό συνεχίζεται εναλλάξ μέχρι οι παλάμες να συναντηθούν στο κέντρο. Όταν όμως απομακρύνουμε τις παλάμες μας από το κέντρο, η πρώτη παλάμη που θα κινηθεί δέχεται ήδη λιγότερο βάρος, άρα λιγότερη τριβή και συνεχίζει έτσι μέχρι να φθάσει στην άκρη καθώς δέχεται συνεχώς μειούμενο βάρος. 

47. Δύο ποδηλάτες κινούνται ο ένας προς τον άλλο, έχοντας ο καθένας σταθερή ταχύτητα 2 m/s. Τη στιγμή που απέχουν μεταξύ τους 100 m, ένας σκύλος ξεκινώντας από τον έναν ποδηλάτη τρέχει συνεχόμενα από τον έναν στον άλλο.

Αν θεωρήσουμε την ταχύτητα του σκύλου σταθερή και ίση με 10 m/s και ότι στρίβει αλλάζοντας κατεύθυνση ακαριαία, πόση απόσταση θα έχει διατρέξει ο σκύλος μέχρι οι ποδηλάτες να συναντηθούν?

    ΑΠ. Αν και φαίνεται σαν ένα δύσκολο μαθηματικό πρόβλημα που απαιτεί την άθροιση μιας ακολουθίας, στην πραγματικότητα είναι πολύ απλό, αν υπολογίσουμε πρώτα τον χρόνο που θα κάνουν οι ποδηλάτες να συναντηθούν και  μετά να χρησιμοποιήσουμε τον χρόνο αυτόν για να υπολογίσουμε την απόσταση που θα έχει τρέξει ο σκύλος.

Έτσι, χρόνος = απόσταση / ταχύτητα σύγκλισης ποδ. = 100m / 4m/s = 25s.

Απόσταση σκύλου = ταχύτητα σκύλου Χ χρόνο = 10m/s X 25s = 250m.

Και ένα σχετικό "ανέκδοτο" που τονίζει την εξαιρετική ικανότητα για υπολογισμούς "με το μυαλό" του μαθηματικού John von Neumann (1903-1957, Ουγγρο-αμερικανός ιδιοφυής μαθηματικός και πρωτοπόρος των ηλεκτρονικών υπολογιστών): 

Ένα συνεργάτης του, ανέφερε στον von Neumann το παραπάνω πρόβλημα. Ο μαθηματικός σκέφτηκε για λίγο και μετά έδωσε τη σωστή απάντηση.

- "Βλέπω ότι ήξερες την εύκολη λύση", του λέει ο φίλος του.

- "Ποια εύκολη λύση;" απαντάει ο von Neumann. "Πρόσθεσα την ακολουθία".

48. Ένας φυλακισμένος είναι σ’ ένα κελί με δύο ίδιες πόρτες εξόδου, μία που οδηγεί στην ελευθερία και μία στον θάνατο. Σε κάθε πόρτα υπάρχει ένας φρουρός και το μόνο που ξέρει ο φυλακισμένος είναι ότι ο ένας απ’ αυτούς λέει πάντα την αλήθεια, ενώ ο άλλος πάντοτε ψέμα.

Στον φυλακισμένο έχει δοθεί η ευκαιρία να διαλέξει την πόρτα εξόδου, και το δικαίωμα να κάνει σ’ έναν από τους φρουρούς μία μόνον ερώτηση. Θα μπορέσει ο φυλακισμένος να εξασφαλίσει τη σωτηρία του?

    ΑΠ. Ναι, αν κάνει μια ερώτηση που η απάντησή της θα περιέχει τις απαντήσεις και των δύο φρουρών, επειδή μία αλήθεια συν ένα ψέμα κάνουν πάντα ένα ψέμα. Έτσι λοιπόν θα μπορούσε να ρωτήσει οποιονδήποτε από τους φρουρούς:

«Αν ρωτούσα τον άλλον φρουρό, πια πόρτα θα μου έδειχνε για να σωθώ?»

Καθώς η απάντηση θα περιέχει την αλήθεια του ενός φρουρού και το ψέμα του άλλου, ο φυλακισμένος θα έπρεπε να διαλέξει την άλλη πόρτα από αυτή που θα του υποδεικνύονταν.

49. Είναι γνωστό ότι τα αυτοκίνητα της Φόρμουλα Ένα (F1) δέχονται σημαντική πρόσθετη δύναμη προς τα κάτω από τις εμπρός και πίσω πτέρυγες που διαθέτουν, σε σημείο που με ταχύτητα ακόμα και 150 km/h η δύναμη αυτή να ξεπερνά το βάρος του οχήματος.

Αυτό σημαίνει ότι τα αυτοκίνητα της F1 θα μπορούσαν να κινηθούν ανάποδα με την ταχύτητα αυτή στην οροφή ενός τούνελ? (Ας μην αναρωτηθούμε προς το παρόν, πώς βρέθηκαν εκεί).

    ΑΠ. Όχι, επειδή οι πτέρυγες αυτές δημιουργούν ταυτόχρονα και μεγάλη οπισθέλκουσα, οπότε για να διατηρήσει το όχημα αυτή την ταχύτητα κινούμενο ανάποδα, θα πρέπει οι τροχοί του να αναπτύσσουν αρκετή πρόσφυση (τριβή).

Αυτό σημαίνει ότι η δύναμη που το πιέζει στην οροφή θα πρέπει να είναι σημαντικά μεγαλύτερη από το βάρος του, άρα η ανάποδη κίνηση θα μπορούσε πράγματι να συμβεί, αλλά σε πολύ μεγαλύτερες ταχύτητες. (Στην εικόνα κάτω, το αυτοκίνητο κάνει πράγματι περιστροφή στην οροφή του τούνελ, αλλά είναι η αντίδραση στην κεντρομόλο που το κρατά σε επαφή με τα τοιχώματα του τούνελ). 

50. Πώς μπορούμε να «εξαφανίσουμε» ένα μικρό γυάλινο σκεύος πυρέξ μπροστά στα μάτια των παρευρισκομένων, χωρίς να παρεμβάλλουμε κάποιο αδιαφανές αντικείμενο και χωρίς «ταχυδακτυλουργικά»? 

    ΑΠ. Το βυθίζουμε σε ένα μεγαλύτερο γυάλινο σκεύος που περιέχει αρκετή γλυκερίνη ώστε να το καλύψει τελείως.
Επειδή ο δείκτης διάθλασης του πυρέξ και της γλυκερίνης είναι ο ίδιος, το βυθισμένο σκεύος οπτικά θα «εξαφανιστεί». 

51. Ένας τεχνίτης διαμορφώνει στον τόρνο έναν μπρούτζινο άξονα, στον οποίο πρέπει να δώσει μια πολύ συγκεκριμένη διάμετρο. Έχει τελειώσει όμως το σαπουνόνερο που χρησιμοποιείται στις εργαλειομηχανές σαν λιπαντικό για την κοπή, αλλά επειδή η εργασία είναι βιαστική ο τεχνίτης προχωράει χωρίς αυτό. Μόλις ολοκληρώσει την εργασία του, μετράει τον άξονα και διαπιστώνει με ικανοποίηση ότι πέτυχε ακριβώς τη διάσταση που έπρεπε, οπότε στέλνει αμέσως τον άξονα στον πελάτη. Η έκπληξή του όμως είναι μεγάλη, όταν την επόμενη ημέρα του επιστρέφεται ο άξονας με την παρατήρηση ότι η διάμετρός του δεν είναι σωστή. Τι έχει συμβεί?

    ΑΠ. Το σαπουνόνερο πέρα από λιπαντικό λειτουργεί και σαν ψυκτικό. Όταν ο τεχνίτης μέτρησε τη διάμετρο του άξονα αμέσως μετά την κατεργασία του, ο άξονας ήταν αρκετά ζεστός και είχε διασταλεί. Όταν κρύωσε λοιπόν, η διάμετρός του βρέθηκε μικρότερη απ’ αυτή που έπρεπε. 

52. Πώς μπορεί να γίνει δίκαια μοιρασιά με «το μάτι», όταν δύο άτομα πρέπει να μοιράσουν μία ομοιογενή ποσότητα? 

    ΑΠ. Ο πρώτος μοιράζει την αρχική ποσότητα σε δύο ίσα (κατά την κρίση του) μέρη, αλλά ο δεύτερος επιλέγει πρώτος ποιο μέρος θα πάρει.

53. Στις ταινίες βλέπουμε να πυροβολείται ένας άνθρωπος και να τινάζεται εντυπωσιακά προς τα πίσω. Αυτό βέβαια είναι υπερβολικό, αλλά αν ένας άνθρωπος αντί να πυροβοληθεί με κανονική σφαίρα πυροβοληθεί με λαστιχένια (ίδιου βάρους και ταχύτητας με την κανονική) θα δεχτεί μεγαλύτερη ώθηση προς τα πίσω? (θεωρούμε ότι η κανονική δεν του προκαλεί διαμπερές τραύμα).

    ΑΠ. Η λαστιχένια θα τον ωθήσει περισσότερο, επειδή όχι μόνο θα μεταφέρει όλη την κινητική της ενέργεια και ορμή στο σώμα του (όπως η κανονική σφαίρα), αλλά επιπλέον θα αναπηδήσει προς τα πίσω εξαιτίας της ελαστικής πρόσκρουσης. 

54. Ένα βάρος λίγων κιλών κρέμεται από έναν σπάγκο από το ταβάνι. Ένας ίδιος σπάγκος είναι δεμένος και στο κάτω μέρος του βάρους και κρέμεται ελεύθερα.
Οι σπάγκοι έχουν αντοχή σε θραύση αρκετά μεγαλύτερη από το βάρος που κρέμεται.
Μπορούμε να καταφέρουμε τραβώντας τον κάτω σπάγκο, να κόβεται άλλοτε ο επάνω σπάγκος και άλλοτε ο κάτω? 

    Απ. Αν τραβήξουμε τον κάτω σπάγκο αργά θα κοπεί ο επάνω σπάγκος, επειδή στη δύναμη που εφαρμόζουμε στον επάνω σπάγκο προστίθεται και η δύναμη του βάρους. Αν τραβήξουμε όμως απότομα τον κάτω σπάγκο θα κοπεί ο ίδιος, επειδή εξαιτίας της αδράνειάς του το βάρος «απορροφά» ένα μέρος της δύναμης τραβήγματος και δεν την αφήνει να εφαρμοστεί όλη στον επάνω σπάγκο.

55. Έχουμε στη διάθεσή μας δύο εξωτερικά πανομοιότυπες μεταλλικές ράβδους, γνωρίζουμε όμως ότι μία απ’ αυτές είναι μαγνήτης. Χωρίς να χρησιμοποιήσουμε οποιοδήποτε άλλο υλικό, πώς μπορούμε να διαπιστώσουμε ποια από τις δύο ράβδους είναι ο μαγνήτης?

    ΑΠ. Ακουμπάμε τις δύο ράβδους μεταξύ τους, ώστε να σχηματίσουν ένα Τ. Αν οι ράβδοι έλκονται ισχυρά στο σημείο επαφής τους, τότε η ράβδος που σχηματίζει το Ι του Τ είναι ο μαγνήτης. Αλλιώς είναι η άλλη που σχηματίζει το οριζόντιο τμήμα του Τ. (Ο μαγνητισμός εκδηλώνεται ουσιαστικά στα άκρα της μαγνητικής ράβδου).

56. Ένας άντρας κάθεται σε μία βάρκα που βρίσκεται μέσα σε μία μικρή λίμνη. Μέσα στη βάρκα υπάρχει και ένα αρκετά μεγάλος βράχος, τον οποίο κάποια στιγμή ο άντρας καταφέρνει να τον πετάξει μέσα στη λίμνη, οπότε ο βράχος εξαφανίζεται κάτω από την επιφάνεια. Θα αλλάξει η στάθμη της λίμνης και πόσο?

    ΑΠ. Η στάθμη θα κατέβει, επειδή όταν ο βράχος βυθιστεί τελείως θα εκτοπίζει λιγότερο νερό από πριν, που ουσιαστικά έπλεε, αν και μέσα στη βάρκα.

57. Έχουμε δύο θερμαντικές αντιστάσεις ίδιων χαρακτηριστικών. Πώς πρέπει να τις συνδέσουμε σε μία πηγή τάσης, ώστε να θερμάνουν γρηγορότερα το περιβάλλον?

    ΑΠ. Πρέπει να τις συνδέσουμε παράλληλα, επειδή ο γενικός τύπος ισχύος είναι: P = V² / R, και η παράλληλη σύνδεση μας δίνει τη μικρότερη συνολικά τιμή αντίστασης, άρα σύμφωνα με τον τύπο την μέγιστη ισχύ. Δηλαδή στην ουσία την κάθε αντίσταση τη συνδέουμε με την πηγή, που είναι το ίδιο με το τις συνδέσουμε πρώτα παράλληλα και μετά με την πηγή.

58. Ένα κανόνι πολύ μεγάλου βεληνεκούς ρίχνει οβίδες με κατεύθυνση από βορρά προς νότο. Παρά την προσεκτική στόχευση όμως με τη βοήθεια χάρτη και πυξίδας (ο στόχος είναι εκτός οπτικής επαφής), διαπιστώνεται ότι τα σημεία πρόσκρουσης των βλημάτων παρουσιάζουν σημαντική απόκλιση από το στόχο, στον άξονα ανατολής – δύσης. Τι συμβαίνει?

    ΑΠ. Δεν έχει ληφθεί υπόψη η απόκλιση εξαιτίας του φαινομένου Coriolis. Αυτό έχει συμβεί στην πραγματικότητα, όταν οι Γερμανοί κατά τον Α΄ Παγκόσμιο Πόλεμο βομβάρδιζαν το Παρίσι από απόσταση 120 χιλιομέτρων, με κανόνια πολύ μεγάλου βεληνεκούς. Η θέση των κανονιών ήταν βορειoανατολικά του Παρισιού και αν δεν γίνονταν διόρθωση για το φαινόμενο Coriolis, οι βολές έπεφταν ένα χιλιόμετρο δυτικότερα από τον στόχο. Η διαφορά οφείλεται στο γεγονός ότι καθώς το βλήμα αφήνει την κάννη του κανονιού, έχει και πλάγια (ανατολική) ταχύτητα εξαιτίας της περιστροφής της Γης. Καθώς όμως το βλήμα κινείται νοτιότερα, συναντά περιοχές που κινούνται προς τα ανατολικά πιο γρήγορα από το ίδιο, επειδή η Γη στην περιοχή του στόχου έχει μεγαλύτερη διάμετρο (ως προς τον άξονα περιστροφής της), άρα το έδαφος εκεί κινείται με μεγαλύτερη ταχύτητα ανατολικά απ’ ότι στην περιοχή που βρίσκεται το κανόνι.

(Στην εικόνα κάτω η βολή γίνεται από τον νότο προς τον βορρά, οπότε η απόκλιση είναι ανατολική).

59. Ένας ναυαγός βρίσκεται στην ταραγμένη θάλασσα με μόνο βοήθημα πλεύσης ένα δοχείο με αρκετά φαρδύ στόμιο, αλλά χωρίς καπάκι. Πως πρέπει να κρατήσει το δοχείο ώστε να τον βοηθήσει να επιπλεύσει ευκολότερα?

    ΑΠ. Ανάποδα, δηλαδή με στόμιο προς τα κάτω, επειδή έτσι θα εγκλωβίσει αέρα που δεν θα τον χάσει. Αν το κρατήσει με το στόμιο προς τα επάνω, αργά ή γρήγορα θα γεμίσει νερό.

60. (Πραγματικό συμβάν). Ένας ηλεκτρολόγος ερευνά γιατί ένα ηλεκτρικό παράθυρο σ’ ένα αυτοκίνητο δεν δουλεύει προς μία κατεύθυνση. Αποσυνδέει το φις τροφοδοσίας από το μοτέρ του παράθυρου και με ένα ηλεκτρονικό βολτόμετρο μετρά για παρουσία τάσης, ενώ φυσικά πατάει το αντίστοιχο κουμπί κίνησης του παράθυρου. Το βολτόμετρο δείχνει παρουσία κανονικής τάσης σ’ αυτή τη μέτρηση. Δεδομένου ότι το παράθυρο δουλεύει προς την άλλη κατεύθυνση, άρα δεν είναι μπλοκαρισμένο ούτε το μοτέρ καμένο, τι μπορεί να συμβαίνει?

    ΑΠ. Μπορεί να υπάρχει κακή επαφή στον διακόπτη, δηλαδή αυξημένη αντίσταση στη διέλευση του ρεύματος. Στην περίπτωση αυτή, το ελάχιστο ρεύμα που χρειάζεται ένα ηλεκτρονικό βολτόμετρο για να έχει ένδειξη μπορεί να περνάει, αλλά όταν πάει να περάσει το πολύ περισσότερο ρεύμα που απαιτεί η λειτουργία του παράθυρου, η πτώση τάσης (που είναι ανάλογη της έντασης του ρεύματος για δεδομένη αντίσταση) δεν αφήνει να φθάσει αρκετή τάση στο μοτέρ. Μία μέτρηση με ένα κλασικό βολτόμετρο που δουλεύει με μεγαλύτερη ένταση (ή ακόμα καλύτερα χρησιμοποιώντας ένα ενδεικτικό λαμπάκι), θα έδειχνε την ουσιαστική απουσία τάσης στο πάτημα του διακόπτη του παράθυρου. 

61. Ένας πύραυλος ανυψώνεται από την εξέδρα εκτόξευσης και παρότι οι κινητήρες του παράγουν σταθερή ώση, η επιτάχυνσή του αυξάνεται. Σε ποιους παράγοντες οφείλεται αυτό;

    ΑΠ. Στην μείωση της πυκνότητας του αέρα με το ύψος, στη μείωση της βαρύτητας (g) με την απομάκρυνσή του από την επιφάνεια της Γης, αλλά κυρίως στη γρήγορη και συνεχή μείωση της μάζας του καθώς καταναλίσκεται το καύσιμό του (το αρχικό καύσιμο αποτελεί τυπικά το 90% της μάζας ενός πυραύλου μαζί με το φορτίο του). Αλλά και οι πυραυλοκινητήρες του, παρότι συνεχίζουν να καίνε καύσιμο με σταθερό ρυθμό, αυξάνουν λίγο την ώση τους επειδή μειώνεται η πίεση της ατμόσφαιρας στην έξοδο των καυσαερίων.

62. Ένα μπαλόνι που περιέχει ήλιο και είναι πολύ ελαστικό ώστε να διαστέλλεται χωρίς να ασκεί πίεση στο ήλιο που περιέχει, πόσο ψηλά μπορεί να φθάσει;

    ΑΠ. Πρακτικά μέχρι τα όρια της ατμόσφαιρας, εφόσον το ήλιο θα διαστέλλεται ελεύθερα και θα βρίσκεται πάντα στην πίεση του περιβάλλοντος (οπότε πάντα θα είναι ελαφρύτερο από τον περιβάλλοντα αέρα). Γι’ αυτό τα μετεωρολογικά μπαλόνια μεγάλου υψομέτρου φαίνονται σαν «άδεια» κοντά στο έδαφος.  Ένα συνηθισμένο μπαλόνι όμως, ασκεί πίεση στο αέριο που περιέχει, η οποία αυξάνεται καθώς το μπαλόνι διαστέλλεται, έτσι η άνοδός του σταματάει σχετικά νωρίς.

63. Κατά πόσο αυξάνεται (χοντρικά) η δυνατότητα αποδιδόμενης ισχύος μιας ανεμογεννήτριας, όταν διπλασιάζεται η ταχύτητα του ανέμου; Χ2, Χ4 ή Χ8; (Στην εικόνα κάτω, οι δίνες του αέρα μετά τις ανεμογεννήτριες γίνονται ορατές εξαιτίας των συνθηκών υγρασίας και θερμοκρασίας του αέρα. Έτσι γίνεται φανερό ότι μόνο η πρώτη σειρά λειτουργεί σε ομαλή ροή αέρα). 

    ΑΠ. Χ8. Και αυτό επειδή ο διπλασιασμός της ταχύτητας μιας μάζας αέρα τετραπλασιάζει την κινητική του ενέργεια και κατά συνέπεια και την ισχύ που μπορεί να αποδώσει στο ίδιο χρονικό διάστημα. Παράλληλα, ο διπλασιασμός της ταχύτητας του ανέμου σημαίνει ότι διπλάσια μάζα αέρα θα περνάει από τα πτερύγια της ανεμογεννήτριας στο ίδιο χρονικό διάστημα, οπότε ο συνδυασμός των δύο παραγόντων οδηγεί στον οκταπλασιασμό της αποδιδόμενης ισχύος.

64. Πολλά ατυχήματα με αυτοκίνητο σε χιονισμένες περιοχές (όπως φαίνεται από αναρτήσεις στο YouTube) συμβαίνουν κατά τη διάρκεια της νύκτας και ειδικά επάνω σε γέφυρες. Υπάρχει κάποιος ειδικός λόγος γι’ αυτό;

    ΑΠ. Όταν η θερμοκρασία του αέρα την ημέρα είναι κοντά στους μηδέν Κελσίου, το βράδυ πέφτει ακόμα περισσότερο, αλλά η αντίστοιχη θερμοκρασία του καταστρώματος του δρόμου εξαιτίας της θερμοχωρητικότητας του εδάφους μειώνεται λιγότερο. Επάνω στις γέφυρες όμως, καθώς δεν υπάρχει έδαφος από κάτω η θερμοκρασία του καταστρώματος ακολουθεί τη θερμοκρασία του αέρα, με αποτέλεσμα αν αυτή είναι κάτω από το μηδέν ενδεχόμενο χιόνι ή νερό στην επιφάνειά του να παγώσει. Και επειδή ο πάγος βρίσκεται μόνο στο τμήμα της γέφυρας και όχι στην υπόλοιπη διαδρομή, πιάνει τους οδηγούς απροετοίμαστους.

65. Υπάρχει τρόπος να φουσκώσουμε ένα μπαλόνι, χωρίς να στείλουμε μέσα του αέρα με πίεση;

    ΑΠ. Ναι, αν το βάλουμε μέσα σ' ένα κλειστό ανθεκτικό δοχείο, με το στόμιο του μπαλονιού να στερεώνεται στεγανά σ' έναν κοντό σωλήνα που διαπερνάει το δοχείο και επιτρέπει την επικοινωνία με τον εξωτερικό χώρο. Αν από μια βαλβίδα ή έναν άλλο σωλήνα που διαπερνά το δοχείο αναρροφήσουμε τον αέρα είτε με αντλία είτε και με το στόμα μας (αν το δοχείο δεν είναι πολύ μεγαλύτερο από το φουσκωμένο μπαλόνι), το μπαλόνι θα φουσκώσει εξαιτίας της διαφοράς των πιέσεων του αέρα μέσα και έξω απ' τα τοιχώματά του. Με αυτή την αρχή δουλεύει ο "σιδερένιος πνεύμονας" στην ιατρική.

66. Κατά την έναρξη του Α’ Παγκοσμίου Πολέμου, η στολή των Βρετανών στρατιωτών περιλάμβανε ένα καφέ καπέλο. Καθώς συνεχιζόταν ο πόλεμος, οι Βρετανοί αξιωματούχοι ανησυχούσαν όλο και περισσότερο για τον αυξανόμενο αριθμό των θυμάτων από βολές στο κεφάλι. Αποφάσισαν να αντικαταστήσουν το καφέ καπέλο με μεταλλικό κράνος. Ωστόσο, προς έκπληξή τους, ο αριθμός των τραυματισμών στο κεφάλι αυξήθηκε παρά το γεγονός ότι η ένταση του πολέμου παρέμεινε ίδια. Γιατί αυξήθηκε ο αριθμός των τραυματισμών στο κεφάλι, παρότι τα καπέλα αντικαταστάθηκαν από μεταλλικά κράνη; (από το https://www.tilestwra.com).

    ΑΠ. Με τα καπέλα οι τραυματισμοί ήταν λιγότεροι, γιατί σχεδόν κάθε βολή στο κεφάλι ήταν θανατηφόρα. Ενώ με τα κράνη, οι βολές στο κεφάλι κατέληγαν μάλλον σε τραυματισμό παρά σε θάνατο.

67. Υπάρχει περίπτωση να δουλέψει ένα σώμα καλοριφέρ που συνδέεται με έναν μόνο σωλήνα;

    ΑΠ. Ναι, αν σωλήνας συνδέεται στο κάτω μέρος του σώματος του καλοριφέρ και τροφοδοτείται με ατμό (καλοριφέρ συμπύκνωσης). Τότε η συμπύκνωση του ατμού, καθώς η θερμότητα του μεταφέρεται στο καλοριφέρ και στη συνέχεια στον αέρα τον υγροποιεί, οπότε επιστρέφει σαν νερό μέσα από τον ίδιο σωλήνα. Η μεγάλη μείωση του όγκου μετά τη συμπύκνωση τραβάει νέο ατμό στο σώμα, που δεν εμποδίζεται από τη μικρή ποσότητα του νερού της συμπύκνωσης που επιστρέφει.

68. Αυτή είναι μια πραγματική ιστορία. Στη διάρκεια του Β’ΠΠ οι Άγγλοι ήθελαν να βομβαρδίσουν με αεροπλάνα, που το καθένα θα μετέφερε μια μεγάλη βόμβα, τα υδροηλεκτρικά φράγματα στο Ρουρ της Γερμανίας. Η ζημιά στο φράγμα θα ήταν μεγαλύτερη αν η βόμβα έσκαγε σε αρκετό βάθος και σε επαφή με τον τοίχο του φράγματος (από την πλευρά της λίμνης). Για να το πετύχουν αυτό, κατασκεύασαν μια κυλινδρική βόμβα που καθώς έπεφτε από το αεροπλάνο που πετούσε σε χαμηλό ύψος, αναπηδούσε στο νερό μέχρι να συναντήσει το χείλος του φράγματος. Η βόμβα όμως πριν ριχτεί από τα αεροπλάνο έμπαινε σε περιστροφή (με 500 rpm) αντίθετα με τη φορά της κίνησής της, σαν να ήθελε δηλαδή να γυρίσει προς τα πίσω. Γιατί; 

    ΑΠ. Καθώς η βόμβα έφτανε στο φράγμα, η προς τα εμπρός κίνησή της σταματούσε αναγκαστικά και άρχιζε να βυθίζεται. Η προς τα πίσω περιστροφή της όμως που συνεχίζονταν εξαιτίας της αδράνειας, σε συνδυασμό με την προς τα κάτω κίνηση δημιουργούσε μια δύναμη (όπως στις «φάλτσες» μπαλιές), που «κόλλαγε» τη βόμβα στα τοιχώματα του φράγματος. Έτσι όταν ένας αισθητήρας βάθους προκαλούσε την έκρηξη, η ζημιά στο φράγμα ήταν η μέγιστη δυνατή. Επιπλέον, η περιστροφή σταθεροποιούσε τη βόμβα ώστε ο άξονάς της να διατηρείται παράλληλος με το νερό κατά τις αναπηδήσεις.

69. Ας υποθέσουμε ότι υπήρχε η δυνατότητα να δημιουργηθεί ένας αόρατος άνθρωπος, με την έννοια ότι θα ήταν τελείως διάφανος. Ποιο θα ήταν ένα σημαντικό πρόβλημά του; 

    ΑΠ. Δεν θα μπορούσε να δει, καθώς για να δει θα έπρεπε οι ακτίνες του φωτός να πέσουν επάνω σε κάτι που θα τις σταματήσει, όπως στον αμφιβληστροειδή του ματιού. Είναι μάλιστα ενδιαφέρον ότι ενώ υπάρχουν πράγματι ορισμένα σχεδόν τελείως διάφανα πλάσματα, συνήθως μικρά ψάρια, μόνο τα μάτια τους είναι αδιαφανή.

70. Είναι λογικό ένα υποβρύχιο να έχει μεγαλύτερη ταχύτητα σε κατάδυση παρά σε ανάδυση?

    ΑΠ. Ναι, παρόλο που σε κατάδυση πρέπει να εκτοπίζει περισσότερο νερό για να προχωρήσει, η δημιουργία κυματισμού όταν κινείται σε ανάδυση απαιτεί μεγαλύτερη δαπάνη ενέργειας. Eπιπλέον το σχήμα των σύγχρονων υποβρυχίων είναι βελτιστοποιημένο για ταχύτητα σε κατάδυση, παρά σε επιφανειακή πλεύση όπως ήταν τα υποβρύχια του Β΄ΠΠ.
Ανάλογη επίδραση έχει και ο "βολβός" στο κάτω μέρος της πλώρης μεγάλων εμπορικών συνήθως πλοίων. Ο βολβός δημιουργεί ένα κύμα λίγο πριν από το σκάφος, με τρόπο ώστε στην ταχύτητα ταξιδιού να βρίσκεται σε μέγιστη διαφορά φάσης με το κύμα που δημιουργεί το ίδιο το σκάφος, μειώνοντάς έτσι την αντίσταση κυματισμού.

Υπάρχει όμως και ένας ακόμα παράγοντας υπέρ των υποβρυχίων σε κατάδυση. Καθώς βρίσκονται κάτω από πολύ μεγαλύτερη υδροστατική πίεση σε σχέση με την πλεύση στην επιφάνεια, η έλικά τους μπορεί να χρησιμοποιεί αρκετά μεγαλύτερη ισχύ για την πρόωσή τους πριν παρουσιαστεί το φαινόμενο της σπηλαίωσης (δημιουργία φυσαλίδων), η οποία περιορίζει σημαντικά την απόδοση των ελίκων.

71.  Δεδομένου ότι οι παλίρροιες οφείλονται κυρίως στην έλξη της Σελήνης (και λιγότερο του Ηλίου) επάνω στις μεγάλες υδάτινες επιφάνειες, και η Σελήνη περνά πάνω από κάθε τόπο χοντρικά κάθε 24 ώρες, γιατί οι πλημμυρίδες (ψηλή στάθμη νερού) συμβαίνουν κάθε 12 ώρες; 

    ΑΠ. Επειδή όταν συμβαίνει πλημμυρίδα σ’ έναν τόπο που έχει από πάνω του τη Σελήνη, στην αντιδιαμετρική πλευρά της Γης συμβαίνει επίσης πλημμυρίδα (αν και μικρότερης έντασης), επειδή στην περιοχή αυτή η έλξη της Σελήνης φτάνει μειωμένη καθώς προστίθεται η διάμετρος της Γης (12.000km).

72. Στα μικρά ελικοφόρα αεροσκάφη που είναι εφοδιασμένα με παλινδρομικούς κινητήρες εσωτερικής καύσης, υπάρχει μία ενδεχόμενα επικίνδυνη κατάσταση όταν περνούν μέσα από ψυχρό και υγρό αέρα. Ο κίνδυνος προέρχεται από την παγοποίηση του καρμπυρατέρ, που μπορεί να προκαλέσει σταμάτημα του κινητήρα. Το πρόβλημα είναι πολύ μικρότερο στα αεροπλάνα που οι κινητήρες τους έχουν αντί για καρμπυρατέρ, σύστημα ψεκασμού. Γιατί; 

    ΑΠ. Η πτώση πίεσης μέσα από τη στένωση του καρμπυρατέρ που υπάρχει κοντά στην πεταλούδα του γκαζιού με σκοπό να τραβάει και να εξαερώνει τη βενζίνη, αλλά κυρίως η ίδια η εξάτμιση της βενζίνης, ψύχουν τον αέρα αρκετά ώστε να συμπυκνώσουν και να παγοποιήσουν την υγρασία του, φράζοντας τελικά τη δίοδο του αέρα (εικόνα κάτω).  Στους κινητήρες με ψεκασμό, η βενζίνη ψεκάζεται είτε αρκετά μετά την πεταλούδα του γκαζιού (έμμεσος ψεκασμός), είτε κατ’ ευθείαν μέσα στον κύλινδρο (άμεσος ψεκασμό), οπότε ο κίνδυνος παγοποίησης είναι μικρότερος. Πάντως όταν οι συνθήκες είναι επικίνδυνες για παγοποίηση, ο πιλότος επιλέγει να τροφοδοτήσει τον κινητήρα με αέρα που θερμαίνεται περνώντας  γύρω από την εξάτμιση, αν και έτσι πέφτει λίγο η απόδοση του κινητήρα, καθώς μειώνεται η πυκνότητα του αέρα.

73. Όπως είναι γνωστό, όταν ένας δορυφόρος είναι σε χαμηλή κυκλική τροχιά γύρω από τη Γη (400-2000km πάνω από την επιφάνειά της) βαθμιαία θα χάσει ύψος και θα μπει στην πυκνότερη ατμόσφαιρα με αποτέλεσμα τελικά να καταστραφεί, εκτός αν περιοδικά διορθώνει την απώλεια ύψους χρησιμοποιώντας τους πυραυλοκινητήρες του. Η απώλεια ύψους συμβαίνει επειδή σταδιακά χάνει ενέργεια από την τριβή του με την σκόνη αλλά και την πολύ αραιή ατμόσφαιρα και άλλα αέρια που υπάρχουν ακόμα και σ’ αυτό το ύψος. Τι συμβαίνει όμως με την ταχύτητά του;

    ΑΠ. Το εκ πρώτης όψεως παράδοξο είναι ότι παρόλο που αυξάνεται η τριβή του με τα αραιότερα στρώματα της ατμόσφαιρας, πρόσκαιρα η γραμμική του ταχύτητα αυξάνεται! Αυτό συμβαίνει επειδή η χαμηλότερη τροχιά απαιτεί μεγαλύτερη ταχύτητα για να διατηρηθεί (έστω και προσωρινά). Η ενέργεια για την αύξηση της ταχύτητας προέρχεται από τη διαφορά με τη χαμηλότερη δυναμική ενέργεια που αντιστοιχεί στο μειωμένο ύψος του δορυφόρου, η οποία «τροφοδοτεί» τόσο την αύξηση της κινητικής του ενέργειας εξαιτίας της αύξησης της ταχύτητας, όσο και την απώλεια ενέργειας σε θερμότητα εξαιτίας των αυξημένων τριβών με την ατμόσφαιρα (ουσιαστικά βέβαια εξαιτίας της συμπίεσης του αέρα).    

74. Αυτή είναι μία πραγματική ιστορία. Σ’ ένα τσίρκο, ένας παλαιστής κυλάει στη σκηνή ένα ψεύτικο κεφάλι τυριού από πλαστικό, διαμέτρου περίπου 80 εκ. και πάχους 20, και προκαλεί οποιονδήποτε από τους θεατές να το ρίξει κάτω. Κανένας δεν τα καταφέρνει, παρότι εμφανώς τίποτα δεν εμποδίζει το τυρί να πέσει, και μόνο στο τέλος ο ίδιος με αρκετή προσπάθεια το ρίχνει κάτω. Τι συνέβαινε;

    ΑΠ. Το ψεύτικο τυρί ήταν κούφιο και έκρυβε ένα βαρύ σφόνδυλο. Ο σφόνδυλος επιταχύνονταν σε ψηλές στροφές στα παρασκήνια, με ένα ηλεκτροκινητήρα που εφάρμοζε σε μία μικρή τρύπα στο κέντρο του τυριού. Το γυροσκοπικό φαινόμενο εμπόδιζε το τυρί να πέσει και μάλιστα αντιδρούσε περίεργα (φυσιολογικά όμως για ένα γυροσκόπιο) όταν το έσπρωχνε κάποιος για να το ρίξει. Μετά από κάποιο διάστημα οι στροφές του είχαν πέσει αρκετά, ώστε ο παλαιστής που δοκίμασε τελευταίος να τα καταφέρει.

75. Ένας «μάγος» τοποθετεί επάνω στο τραπέζι του έναν άδειο μεταλλικό σωλήνα μήκους περίπου 40 εκ., και δύο όμοιους σιδερένιους κυλίνδρους λίγο μικρότερης διαμέτρου από τον σωλήνα και μήκους μερικών εκατοστών, που φροντίζει να τους αφήσει σε κάποια απόσταση μεταξύ τους. Φωνάζει μάλιστα έναν θεατή και του δίνει να κρατήσει σε κάθε χέρι από έναν κύλινδρο, για να διαπιστώσει ότι έχουν το ίδιο βάρος. Λέει ότι θα κάνει ένα πείραμα «αντιβαρύτητας», οπότε κρατάει τον σωλήνα κατακόρυφο και σε κάποια απόσταση από το τραπέζι, καθώς αφήνει τον έναν κύλινδρο να πέσει μέσα του. Ο κύλινδρος πέφτει αμέσως στο τραπέζι μέσα από τον σωλήνα, οπότε ο μάγος τον απομακρύνει και αφήνει τον δεύτερο κύλινδρο να πέσει μέσα από τον σωλήνα, καθώς υποτίθεται έχει ενεργοποιήσει στο μεταξύ ένα αντιβαρυτικό πεδίο. Ο δεύτερος κύλινδρος πράγματι καθυστερεί πολύ να περάσει μέσα από τον σωλήνα, πριν πέσει από την κάτω τρύπα. Ο μάγος γυρίζει τον σωλήνα και τον δείχνει στους θεατές που διαπιστώνουν ότι είναι τελείως άδειος και χωρίς κανένα εμπόδιο. Τι έχει συμβεί;

    ΑΠ. Ο σωλήνας είναι από αλουμίνιο (ή χαλκό), ενώ ο δεύτερος κύλινδρος είναι μαγνήτης. Καθώς κινείται μέσα από τον σωλήνα επάγει επάνω στον σωλήνα δινορρεύματα, που αλληλεπιδρούν με το πεδίο του μαγνήτη με τρόπο ώστε να τον επιβραδύνουν (εικόνα κάτω).

76. Στη διάρκεια του Β’ΠΠ η ισχύς των αεροπορικών κινητήρων αυξήθηκε ραγδαία, φτάνοντας ή και ξεπερνώντας προς το τέλος του τους 2500 ίππους. Δεδομένου ότι τα μονοκινητήρια καταδιωκτικά αεροσκάφη είχαν ουραίο τροχό, πριν οι πιλότοι βρεθούν στον αέρα για να πολεμήσουν, ειδικά αν ήταν κάπως ενθουσιώδεις με το άνοιγμα του γκαζιού, είχαν να αντιμετωπίσουν φυσικές δυνάμεις που προσπαθούσαν (και συχνά τα κατάφερναν εξίσου καλά με τους αντιπάλους τους) να τους εξουδετερώσουν. Μπορείτε να φανταστείτε ποιες ήταν αυτές οι δυνάμεις;

    ΑΠ. Καθώς οι κινητήρες (που συνήθως ήταν δεξιόστροφοι από τη θέση του πιλότου) κινούσαν μεγάλες και βαριές έλικες, το απότομο άνοιγμα του γκαζιού και η επακόλουθη επιτάχυνση της περιστροφής της έλικας, προκαλούσε αντίθετη ροπή στον κινητήρα που συμπίεζε το αριστερό σκέλος του αεροσκάφους αυξάνοντας την τριβή του και εκτρέποντας το αεροσκάφος προς τα αριστερά. Σαν να μην έφτανε αυτό, η αλλαγή στο επίπεδο περιστροφής της έλικας καθώς σηκώνονταν η ουρά πριν την απογείωση, προκαλούσε γυροσκοπική εκτροπή επίσης προς τα αριστερά. Και σαν να μην έφτανε ούτε αυτό, το ρεύμα του αέρα από την έλικα που περιστρέφονταν δεξιόστροφα, πίεζε το ουραίο κάθετο πτερύγιο προς τα δεξιά, συνεισφέροντας και αυτό στην εκτροπή του αεροσκάφους προς τα αριστερά. Όλα αυτά φαίνονται στην εικόνα κάτω.

77. Ένας τεχνίτης τοποθετεί έναν σιδερένιο σωλήνα στο έδαφος, αλλά διαπιστώνει ότι του λείπει ένα μικρό κομμάτι σωλήνα για να συμπληρώσει την εγκατάσταση. Έχει όμως ένα τμήμα χάλκινου σωλήνα που ταιριάζει ακριβώς με τη διάμετρο του σιδερένιου, οπότε ετοιμάζεται να τον χρησιμοποιήσει για να συμπληρώσει το μήκος που λείπει. Ένας συνάδελφός του τού λέει να μην το κάνει, αλλά να πάει να βρει σιδερένιο σωλήνα για το συμπλήρωμα. Ο τεχνίτης νομίζοντας ότι ο λόγος είναι το μεγαλύτερο κόστος του χάλκινου σωλήνα τελικά τον χρησιμοποιεί, καθώς εκτιμά ότι το κομμάτι αυτό είναι πολύ μικρό, συνεπώς άχρηστο για οποιαδήποτε άλλη χρήση. Έκανε καλά;

    ΑΠ. Όχι. Ο συνάδελφός του εννοούσε ότι εφόσον δύο ανόμοια μέταλλα έρχονται σε άμεση αγώγιμη επαφή μεταξύ τους μέσα σε περιβάλλον που ευνοεί την κίνηση ιόντων (όπως το έδαφος, το θαλασσινό νερό κλπ), το λιγότερο «ευγενές» που στην προκειμένη περίπτωση είναι ο σίδηρος, θα υποστεί έντονη ηλεκτροχημική διάβρωση* με συνέπεια σύντομα να τρυπήσει. Μία λύση θα ήταν να παρεμβληθεί ένα πολύ μικρό τμήμα πλαστικού σωλήνα ανάμεσα στους δύο ανόμοιους μεταλλικούς.
*Από το ρεύμα που θα περάσει, καθώς το σύστημα λειτουργεί σαν μπαταρία.

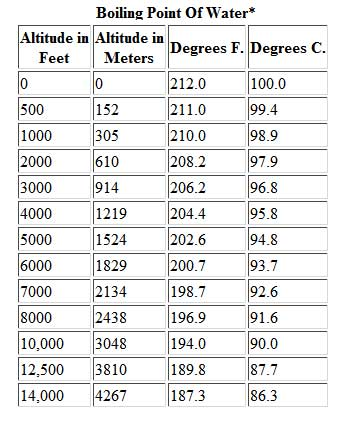
78. Ένα μικρό διθέσιο  ιδιωτικό αεροσκάφος έχει απογειωθεί για μια πρωινή πτήση, και ο φίλος του πιλότου που κάθεται δίπλα του έχει φέρει μαζί του ένα θερμός γεμάτο με πολύ ζεστό καφέ. Όταν το αεροσκάφος φτάνει σε υψόμετρο 12.500 ποδών (3.800 μέτρων), ο φίλος του πιλότου θέλει να του προσφέρει ένα κύπελλο καφέ. Τη στιγμή όμως που ανοίγει το καπάκι του θερμός, ο καφές ξεχύνεται καίγοντάς τον άσχημα. Τι συνέβη;

    ΑΠ. Σε υψόμετρο 3.800 μέτρων (βλέπε πίνακα κάτω) βρίσκουμε ότι το νερό βράζει στους 87.7 βαθμούς Κελσίου. Με το που άνοιξε το καπάκι του θερμός, η πίεση μέσα του εξισώθηκε με την ατμοσφαιρική στο υψόμετρο εκείνο (τα μικρά αεροσκάφη δεν διαθέτουν συμπιεζόμενη καμπίνα) και ο καφές έβρασε απότομα. Για αντίστοιχο λόγο δεν πρέπει να ανοίγουμε το καπάκι από το ψυγείο αυτοκινήτου που έχει ανέβει πολύ η θερμοκρασία του. Το καπάκι κρατάει το κύκλωμα του νερού υπό πίεση, όποτε η θερμοκρασία βρασμού με το καπάκι κλειστό ξεπερνάει τους 100 βαθμούς Κελσίου. Σε μια τέτοια περίπτωση το άνοιγμα του καπακιού θα εξισώσει την πίεση με την ατμοσφαιρική, οπότε το νερό θα βράσει απότομα και θα εκτιναχθεί.

79. Σε κάποιον που θέλει να εργαστεί στο εξωτερικό, του προσφέρεται η δυνατότητα  επιλογής μεταξύ δύο τόπων εργασίας. Ο πρώτος είναι στην Αραβική χερσόνησο με θερμοκρασίες που φθάνουν συχνά τους 42 βαθμούς Κελσίου και σχετική υγρασία γύρω στο 20%, ενώ ο δεύτερος βρίσκεται στη νότια Ασία με θερμοκρασίες που δεν ξεπερνούν τους 35 βαθμούς Κελσίου και σχετική υγρασία συχνά κοντά στο 80%. Δεδομένου ότι ο υποψήφιος εργαζόμενος νοιώθει συχνά δυσφορία με τη ζέστη και η εργασία θα είναι κυρίως εξωτερική, σκοπεύει να επιλέξει τη δεύτερη περιοχή, αλλά ένας φίλος του προτείνει να ελέγξει πρώτα κάτι. Τι του προτείνει;

    ΑΠ. Του προτείνει να ελέγξει έναν πίνακα θερμοκρασίας / υγρασίας που δείχνει και τα επίπεδα άνεσης στον άνθρωπο. Αν κάνει αυτόν τον έλεγχο, θα διαπιστώσει ότι οι συνθήκες στην Αραβική χερσόνησο παρά τις υψηλότερες θερμοκρασίες είναι σαφώς καλύτερα ανεκτές από αυτές της νοτίου Ασίας με την υψηλή υγρασία. Αυτό οφείλεται στο ότι η ψύξη στο ανθρώπινο σώμα προέρχεται κυρίως από την εξάτμιση του ιδρώτα, που όμως εμποδίζεται από την υψηλή υγρασία στην ατμόσφαιρα.

80. Αν γεμίσουμε ένα μικρό αερόστατο από κατάλληλο θερμοάντοχο υλικό και ανοικτό στο κάτω μέρος του με θερμό αέρα 150 βαθμών Κελσίου, και ένα δεύτερο όμοιο αερόστατο με ατμό της ίδιας θερμοκρασίας και τα ελευθερώσουμε, ποιο θα ανέβει ψηλότερα;

    ΑΠ. Το αερόστατο ατμού, επειδή ο ατμός είναι λίγο ελαφρύτερος από αέρα ίδιας θερμοκρασίας, και επιπλέον καθώς θα ψύχεται και συμπυκνώνεται θα απελευθερώνει τη λανθάνουσα θερμότητά του, με αποτέλεσμα να επιβραδύνεται η ψύξη του.

81. Μπορεί ένας θαλάσσιος σκιέρ που σύρεται από σκάφος που κινείται με σταθερή ταχύτητα και σε ευθεία πορεία, να κινηθεί με μεγαλύτερη ταχύτητα από το σκάφος; (Όχι να ξεπεράσει το ίδιο το σκάφος).

    ΑΠ. Ναι, αν κινηθεί προς τα πλάγια της πορείας του σκάφους, κάτι που οι έμπειροι σκιέρ το κάνουν συστηματικά. Με αυτόν τον τρόπο η ταχύτητά του θα γίνει η συνισταμένη της ταχύτητας του σκάφους και της κάθετης ταχύτητάς του προς την πορεία του σκάφους, που φυσικά θα είναι μεγαλύτερη από κάθε μία από τις συνιστώσες της. Βέβαια, δεν θα μπορέσει ποτέ να ξεπεράσει το ίδιο το σκάφος, το πολύ-πολύ να έλθει σχεδόν στο ίδιο ύψος με αυτό (οπότε, καθώς η πλάγια κίνηση σταματάει, η ταχύτητά του γίνεται πάλι ίση με του σκάφους). Θα απαιτηθεί όμως μεγάλη δύναμη έλξης από τον σκιέρ, καθώς η πλάγια κίνησή του προκύπτει από την κλίση που θα δώσει στα (ή στο) σκι του ως προς το νερό, ώστε να «χαράξουν» πλάγια πορεία, καθώς έτσι αυξάνεται σημαντικά η αντίστασής τους στην προς τα εμπρός κίνηση.

82. Μία ποδοσφαιρική ομάδα προπονείται σ’ ένα ανοικτό γήπεδο όταν στην περιοχή ξεσπά καταιγίδα με κεραυνούς. Οι παίκτες περπατούν βιαστικά προς τα αποδυτήρια, αλλά ο προπονητής τους τούς λέει να πάνε χοροπηδώντας από το ένα πόδι στο άλλο. Γιατί;

    ΑΠ. Επειδή στην περίπτωση που πέσει κεραυνός κοντά τους, κινδυνεύουν από ηλεκτροπληξία εξαιτίας της «βηματικής τάσης», της τάσης δηλαδή που αναπτύσσεται μεταξύ δύο σημείων στο έδαφος όταν δημιουργείται διαφορά δυναμικού, όπως από την πτώση κεραυνού. Αν όμως τα πόδια είναι ενωμένα ή στηρίζεται κάποιος μόνο στο ένα πόδι κάθε φορά, χωρίς ποτέ να ακουμπούν ταυτόχρονα στο έδαφος, τότε ο κίνδυνος ελαχιστοποιείται. (Στην εικόνα χτύπημα κεραυνού στο έδαφος. Κατά μήκος των ιχνών, η τάση μεταβάλλεται κατά πολύ).

83. Πώς θα μεταβληθεί το ύψος ενός αντικειμένου που επιπλέει μέσα σ' ένα δοχείο με νερό, από τον πυθμένα του δοχείου, αν θερμάνουμε το νερό;  Θα σκεφθεί κάποιος ότι το αντικείμενο θα ανέβει, αφού το νερό θα διασταλεί, αλλά θα πρέπει να λάβει υπόψη ότι και το αντικείμενο θα βυθιστεί περισσότερο καθώς η πυκνότητα του νερού θα μειωθεί. 

    ΑΠ. Δεν υπάρχει μία απάντηση, εξαρτάται βασικά από τις διαστάσεις του δοχείου και του αντικειμένου. Αν το δοχείο είναι μεγάλο με μικρό βάθος, η αύξηση του ύψους του νερού θα είναι μικρή (αφού η διαστολή επηρεάζει τον όγκο), και η μεγαλύτερη βύθιση του αντικειμένου θα μειώσει το συνολικό του ύψος από τον πυθμένα. Αντίθετα, σ' ένα στενό και ψηλό δοχείο, η αύξηση του ύψους του νερού θα είναι σημαντική και η απόσταση του αντικειμένου από τον πυθμένα τελικά θα αυξηθεί.

84. Ένας ηλεκτρολόγος έχει στη διάθεσή του δύο αντιστάσεις διαφορετικής τιμής, πχ 10 και 15 Ωμ αντίστοιχα, για να κατασκευάσει μια συσκευή θέρμανσης. Πόσες "σκάλες" θέρμανσης μπορεί να έχει η συσκευή του, και χωρίς υπολογισμούς, πότε θα πάρει τη μικρότερη και πότε τη μεγαλύτερη ισχύ; 

    ΑΠ. Μπορεί να έχει τέσσερις σκάλες, δηλαδή κάθε αντίσταση μόνη της, και συνδεδεμένες είτε σε σειρά είτε παράλληλα. Τη μικρότερη ισχύ θα την πάρει με την σε σειρά σύνδεση (μέγιστη συνολική αντίσταση), και τη μεγαλύτερη με την παράλληλη σύνδεση (ελάχιστη συνολική αντίσταση).

85. Αν ένας αστροναύτης σε τροχιά πυροβολήσει τελείως οριζόντια (ουσιαστικά κάθετα στην ευθεία που τον συνδέει με τον άξονα της Γης) και προς την κατεύθυνση της κίνησής του, μπορεί να τραυματίσει τον εαυτό του;

    ΑΠ. Υποτίθεται ότι το βλήμα θα κάνει τον γύρο της Γης και μπορεί να τον ξανασυναντήσει, τραυματίζοντάς τον. Όμως αυτό δεν μπορεί να γίνει, γιατί η πρόσθετη κινητική ενέργεια που θα αποκτήσει το βλήμα με την εκπυρσοκρότηση θα το ανεβάσει σε ψηλότερη τροχιά, μειώνοντας ταυτόχρονα την ταχύτητά του. Με αυτόν τον τρόπο άλλωστε ανεβάζουν το επίπεδο τροχιάς τους οι δορυφόροι, ενεργοποιώντας δηλαδή τους προωθητήρες τους. Αντίστοιχα, η ανάκρουση της εκπυρσοκρότησης θα επιβραδύνει λίγο τον αστροναύτη μειώνοντας το ύψος τροχιάς του και αυξάνοντας κατά συνέπεια την ταχύτητά του. Με παρόμοιο τρόπο επιστρέφουν τα διαστημόπλοια από τροχιά, στη Γη.

86. Ένα επιβατικό αεροπλάνο συνήθως ταξιδεύει σε ύψος περίπου 10 km. Η εξωτερική θερμοκρασία στο ύψος αυτό είναι γύρω στους -50 βαθμούς Κελσίου. Είναι συνεπώς αναμενόμενο ότι εξαιτίας της συστολής, το μήκος του αεροπλάνου θα έχει (ως προς την κατάσταση εδάφους), έστω και ελάχιστα μειωθεί. Σωστά;

    ΑΠ. Σωστά. Αν και η διαφορά πίεσης μέσα και έξω από την καμπίνα τείνει να την επιμηκύνει, πρόκειται μόνο για μερικά χιλιοστά.  Αντίθετα, η βράχυνση της καμπίνας εξαιτίας της διαφοράς θερμοκρασίας από +20 σε -50 (70 βαθμοί συνολικά) είναι μερικά εκατοστά! και προφανώς επικρατεί.

87. Είναι γνωστό ότι οι πιλότοι των μαχητικών αεροσκαφών κινδυνεύουν να λιποθυμήσουν αν οι δυνάμεις της κεντρομόλου θετικής επιτάχυνσης (που τους κολλάνε δηλαδή στο κάθισμα) στη διάρκεια μιας στροφής πλησιάσουν τα 9g, δηλαδή 9 φορές τη γήινη επιτάχυνση. Όσοι όμως έχουν παρακολουθήσει αγώνες αεροσκαφών Red Bull θα έχουν δει ότι μπορούν να φτάσουν και τα 12g (αν και τότε ακυρώνονται) και μάλιστα κάποιοι απ’ αυτούς δεν είναι καν νέοι. Πώς γίνεται αυτό?

    ΑΠ. Τα αεροσκάφη των αγώνων Red Bull είναι πολύ μικρότερα, ελαφρύτερα, βραδύτερα και με πολύ μικρότερη ισχύ από τα μαχητικά. Έτσι οι στροφές τους είναι μεν πολύ κλειστές και αναπτύσσονται πολλά g, αλλά είναι σύντομες και o εγκέφαλος έχει αρκετά αποθέματα οξυγόνου για μέχρι περίπου 3 sec. Βέβαια τόσο οι πιλότοι των μαχητικών όσο και των αεροσκαφών Red Bull φοράνε ειδικές στολές anti-g (ενεργές οι πρώτοι με πίεση αέρα, παθητικές οι δεύτεροι με μετατόπιση νερού) και επίσης εφαρμόζουν ειδικές τεχνικές αναπνοής.

88. Στη διάρκεια του Β’ΠΠ φάνηκε η ανάγκη για πτήση σε όλο και μεγαλύτερο υψόμετρο. Το πρόβλημα του αραιότερου αέρα για τους εμβολοφόρους κινητήρες αντιμετωπίσθηκε με υπερσυμπιεστές μιας ή και δύο βαθμίδων. Με την αραίωση όμως του αέρα του περιβάλλοντος διαπιστώθηκε ότι τα κυκλώματα υψηλής τάσης παρουσίαζαν σημαντική ηλεκτρική διαρροή (νόμος Paschen), με αποτέλεσμα να μη φθάνει αρκετή τάση στα μπουζί των κινητήρων ώστε να γίνει ο σπινθήρας. Ποια λύση φαντάζεστε ότι δόθηκε; 

    ΑΠ. Θα μπορούσαν να αυξήσουν τις διαστάσεις των μονωτικών υλικών, αλλά αυτό θα πρόσθετε όγκο, βάρος και θα απαιτούσε πλήρη ανασχεδιασμό. Αντίθετα επέλεξαν να κλείσουν τα μανιατό (γεννήτριες παραγωγής υψηλής τάσης) και τα καλώδιά τους σε αεροστεγείς θήκες (με ανακουφιστική βαλβίδα υπερπίεσης) και να τα τροφοδοτήσουν με πεπιεσμένο αέρα από τον (ή τους) υπερσυμπιεστές του κινητήρα. 

89. Από το επάνω μέρος ενός κλειστού αδιαφανούς κουτιού προεξέχουν κάθετα και για μερικά εκατοστά δύο όμοιοι σωλήνες, που και μεταξύ τους απέχουν μερικά εκατοστά. Η διάμετρος των σωλήνων είναι περίπου ένα εκατοστό και γνωρίζουμε ότι συνεχίζονται ευθύγραμμα μέσα στο κουτί, χωρίς φυσικά αυτό το τμήμα τους να είναι ορατό. Γνωρίζουμε επίσης ότι το άκρο τους μέσα στο κουτί είναι ταπωμένο και ότι δεν έχουν το ίδιο μήκος. Χωρίς να χρησιμοποιήσουμε οποιοδήποτε εργαλείο, υγρό κλπ και χωρίς να μετακινήσουμε το κουτί, μπορούμε να βρούμε ποιος είναι  ο μακρύτερος και ποιος ο κοντύτερος;

    ΑΠ. Θα φυσήξουμε παράλληλα και κοντά στο άνοιγμα του κάθε σωλήνα και προσέξουμε τη συχνότητα του ήχου που θα παραχθεί. Ο βαρύτερος ήχος θα αντιστοιχεί στον μακρύτερο σωλήνα και ο οξύτερος στον κοντύτερο. Στην εικόνα κάτω, αντίστοιχο πείραμα με μπουκάλια με διαφορετική στάθμη νερού.

90. Αυτό είναι από συμβουλές οδήγησης εκτός δρόμου. Ένα όχημα κινείται εγκάρσια σε μια ομαλή αλλά με μεγάλη κλίση πλαγιά ενός λόφου, δηλαδή χωρίς να ανεβαίνει ή να κατεβαίνει.  Ξαφνικά, εξαιτίας μιας τοπικής αύξησης στην κλίση του εδάφους που πέρασε απαρατήρητη, ο οδηγός διαπιστώνει ότι το όχημα πάει να τουμπάρει, δηλαδή νιώθει ότι οι τροχοί που βρίσκονται προς το επάνω μέρος της πλαγιάς ανασηκώνονται. Πως πρέπει να αντιδράσει;

    ΑΠ. Θα πρέπει να στρίψει ελαφρά το τιμόνι προς το κάτω μέρος της πλαγιάς και ταυτόχρονα να επιταχύνει*. Αυτό θα δημιουργήσει μια αντίδραση στην κεντρομόλο επιτάχυνση της στροφής (με απλά λόγια μια "φυγόκεντρο" δύναμη) που θα ξαναβάλει τους τροχούς σε επαφή με το λόφο, ώστε με λίγη τύχη να ξεπεραστεί η τοπική ανωμαλία του εδάφους.
*Θα μπορέσει να επιταχύνει, αν το σύστημα κίνησης του οχήματος μπορεί να μεταφέρει ροπή, με τους τροχούς της μιας πλευράς ουσιαστικά στον αέρα.

91. Παίρνουμε ένα κερί και το διαπερνούμε κάθετα στο κέντρο του με μια αρκετά μεγάλη βελόνα, έτσι ώστε να δημιουργηθεί ένας λεπτός άξονας που προεξέχει κατά ένα τουλάχιστον εκατοστό από την κάθε πλευρά. Αποκαλύπτουμε ίσο μήκος φιτιλιού στα δύο άκρα του κεριού και ακουμπάμε τον άξονα στα χείλη δύο ποτηριών, ελέγχοντας ότι το κερί ισορροπεί οριζόντια. Ανάβουμε τα δύο άκρα του κεριού. Τι θα συμβεί;

    ΑΠ. Στην αρχή το κερί θα παραμείνει οριζόντιο καθώς καίγονται τα δύο άκρα του. Όταν το λιωμένο κερί θα αρχίσει να στάζει, θα ξεκινήσει μια μικρή ταλάντωση που θα γίνεται όλο και πιο έντονη καθώς η πλευρά που χαμηλώνει κάθε φορά θα αδειάζει περισσότερο από λιωμένο κερί (και η φλόγα θα πλησιάζει περισσότερο τον κορμό λιώνοντας ακόμα περισσότερο κερί), κάνοντας την πλευρά αυτή ελαφρύτερη, ώστε στη συνέχεια να σηκωθεί ψηλότερα από την άλλη. Αυτή η ταλάντωση γίνεται τόσο έντονη, όσο το ύψος των ποτηριών το επιτρέπει.

92. Δύο πανομοιότυπα αυτοκίνητα συγκρούονται έχοντας το καθένα ακριβώς την ίδια ταχύτητα, ακριβώς μετωπικά και τελείως συμμετρικά. Πώς το αποτέλεσμα αυτής της σύγκρουσης συγκρίνεται με τη σύγκρουση του ενός από τα αυτοκίνητα αυτά και με την ίδια ταχύτητα, κάθετα σε άκαμπτο τοίχο;

    ΑΠ. Το αποτέλεσμα είναι το ίδιο, παρόλο που η ταχύτητα προσέγγισης των δύο αυτοκινήτων μεταξύ τους είναι διπλάσια από αυτή της προσέγγισης του ενός αυτοκινήτου στον τοίχο. Αυτό μπορούμε να καταλάβουμε εύκολα, αν φανταστούμε ένα εύκαμπτο διάφραγμα ακριβώς στο σημείο που συναντώνται τα δύο αυτοκίνητα όταν συγκρούονται μεταξύ τους. Το διάφραγμα, εφόσον η σύγκρουση είναι τέλεια συμμετρική δεν έχει λόγο να κινηθεί. Αφαιρούμε τώρα το ένα αυτοκίνητο και το αντικαθιστούμε με έναν άκαμπτο τοίχο ακριβώς σε επαφή με το διάφραγμα. Το αποτέλεσμα της σύγκρουσης του ενός αυτοκινήτου τώρα (με την ίδια ταχύτητα όπως πριν) επάνω στο διάφραγμα πάλι δεν πρόκειται να το μετακινήσει. Ο τοίχος δηλαδή έπαιξε απλά τον ρόλο του δεύτερου αυτοκινήτου.

93. Όλα τα σύγχρονα αυτοκίνητα δοκιμάζονται σε crash test για τον έλεγχο της αντοχής τους σε σύγκρουση και για την προστασία που παρέχουν στους επιβαίνοντες. Το βασικό τεστ περιλαμβάνει μετωπική κατά 50% πρόσκρουση σε σχεδόν άκαμπτο εμπόδιο, με την ίδια για όλα ταχύτητα. Και συμβαίνει συχνά, ένα μικρό αυτοκίνητο να πετυχαίνει την ανώτατη βαθμολογία, όπως και ένα άλλο πολύ μεγαλύτερο και ακριβότερο. Αυτό σημαίνει ότι τα δύο αυτά αυτοκίνητα είναι ισοδύναμα σε περίπτωση σύγκρουσης, σωστά;

    ΑΠ. Ναι, αλλά μόνο εφόσον το καθένα συγκρουστεί μόνο του με άκαμπτο εμπόδιο (και φυσικά με την ίδια ταχύτητα). Αν συγκρουστούν μεταξύ τους, το μεγαλύτερο αυτοκίνητο θα προστατεύσει καλύτερα τους επιβάτες τους καθώς θα τους υποβάλει σε χαμηλότερη επιβράδυνση. Ας φανταστούμε δύο ίδια αυτοκίνητα που κινούνται με την ίδια ταχύτητα και συγκρούονται μετωπικά. Αμέσως μετά τη σύγκρουση το καθένα θα αναπηδήσει ελαφρά προς τα πίσω, καθώς κάθε σύγκρουση είναι κυρίως πλαστική αλλά και λίγο ελαστική. Αν όμως η διαφορά βάρους είναι μεγάλη, το βαρύτερο αυτοκίνητο δεν θα αναπηδήσει καθόλου προς τα πίσω, μάλιστα θα συνεχίσει για λίγο προς την ίδια κατεύθυνση. Το μικρότερο όμως θα αναπηδήσει έντονα προς τα πίσω και προφανώς θα υποβάλει τους επιβάτες τους για τον ίδιο χρόνο (όσο δηλαδή διαρκεί η σύγκρουση) σε πολύ μεγαλύτερη διαφορά ταχύτητας, άρα και σε υψηλότερη επιβράδυνση.

94. Ένα αυτοκίνητο τύπου χάτσμπακ (δηλαδή με "κοφτό" το πίσω μέρος, βλ εικόνα) κινείται σε έναν ευθύ ερημικό δρόμο, όταν ξεσπά έντονη χαλαζόπτωση με χαλάζι μεγάλου μεγέθους. Δεδομένου ότι δεν υπάρχει κάποιο κοντινό σημείο που να προσφέρεται για κάλυψη (υπόστεγο, γέφυρα, δένδρα κλπ), τι πρέπει να κάνει ο οδηγός για να μειώσει τον κίνδυνο να σπάσει κάποιο από τα τζάμια του αυτοκινήτου;  

    ΑΠ. Να κινηθεί με την όπισθεν αρκετά γρήγορα, φυσικά μέσα στα πλαίσια της ασφαλείας και ελπίζοντας ότι η έντονη χαλαζόπτωση θα είναι σύντομη. Έτσι, θα μειωθεί η κάθετη δύναμη που ασκεί η πρόσκρουση κάθε χαλαζόμπαλας στο (συνήθως) έντονα κεκλιμένο παρμπρίζ του αυτοκινήτου, η οποία αντίθετα αυξάνεται με την προς τα εμπρός κίνησή του. Βέβαια, θα αυξηθεί η δύναμη πρόσκρουσης στο πίσω παρμπρίζ, η οποία όμως είναι πολύ μικρότερη καθώς στα χάτσμπακ το πίσω παρμπρίζ είναι σχεδόν κατακόρυφο.

95. Σε μία περιοχή κοντά στον ισημερινό, ένα αερόστατο διαμέτρου μερικών μέτρων αιωρείται ακίνητο σε σχέση με το έδαφος, σε ύψος 10 χιλιομέτρων. Ένα ισχυρό αντιαεροπορικό όπλο που βρίσκεται στο έδαφος και ακριβώς στην ίδια κατακόρυφο, το στοχεύει με σκοπό να το κτυπήσει. Θεωρώντας ότι το βλήμα του αντιαεροπορικού έχει αρκετή αρχική ταχύτητα ώστε να φθάσει στο ύψος του αερόστατου μέσα σε 40 περίπου δευτερόλεπτα, ότι η σκόπευση είναι ακριβέστατη και ότι υπάρχει απόλυτη άπνοια σ' όλη την ατμόσφαιρα, είναι σίγουρο ότι θα το χτυπήσει;

    ΑΠ. Είναι σίγουρο ότι δεν θα το χτυπήσει, επειδή το βλήμα αφήνει την κάννη του όπλου με οριζόντια ταχύτητα που αντιστοιχεί στη γραμμική ταχύτητα του ισημερινού στο επίπεδο του εδάφους. Το αερόστατο για να μένει ακίνητο σε σχέση με το έδαφος και εφόσον βρίσκεται σε αρκετά μεγάλο ύψος, κινείται με σαφώς μεγαλύτερη γραμμική ταχύτητα από αυτή του εδάφους. Έτσι όταν το βλήμα θα φθάσει στο ύψος του αερόστατου θα έχει μείνει αρκετά μέτρα πίσω του (δυτικά του), άρα δεν θα το χτυπήσει.

96. Επάνω σε μία ευαίσθητη ζυγαριά βρίσκεται ένα στεγανό πλαστικό μπουκάλι που περιέχει μόνο μία μύγα. Το μπουκάλι είναι αρκετά μεγάλο για να μπορεί η μύγα να πετάξει χωρίς να αγγίζει τα τοιχώματά του, αλλά αρκετά ελαφρύ ώστε το βάρος της μύγας να διακρίνεται στη ζυγαριά. Αν η μύγα που κάθονταν στο πάτο του μπουκαλιού πετάξει και αιωρηθεί, θα μεταβληθεί η ένδειξη της ζυγαριάς;

    ΑΠ. Όχι, αλλά μόνον εφόσον η μύγα πετάει κοντά στον πάτο. Αρχικά, όταν η μύγα πατάει στον πάτο του μπουκαλιού, το βάρος της φυσικά μεταφέρεται στη ζυγαριά. Όταν πετάει χαμηλά, το βάρος της εξακολουθεί να μεταφέρεται στον πάτο όχι μέσα από τα πόδια της, αλλά από τη ροή του αέρα που προκαλούν τα φτερά της. Αν πετάξει όμως ψηλότερα, η ροή του αέρα καταλήγει σε δίνες, που δεν πιέζουν τον πάτο του μπουκαλιού αλλά θερμαίνουν τον αέρα στο μπουκάλι. Το ενδιαφέρον είναι ότι το πείραμα αυτό έχει γίνει τόσο με πραγματική μύγα όσο και με μικρό drone, και το αποτέλεσμα είναι αυτό που περιεγράφηκε. 

97. Πώς μπορούμε να διαπιστώσουμε με απλά μέσα, ότι κάποιο σημείο μακριά μας βρίσκεται στο ίδιο υψόμετρο με εμάς;

    ΑΠ. Παίρνουμε ένα ποτήρι κατά προτίμηση φαρδύ και με λεία κυλινδρικά τοιχώματα, και του βάζουμε νερό. Το φέρνουμε στο ύψος των ματιών μας και κοιτάζουμε παράλληλα με την επιφάνεια του νερού προς το σημείο που μας ενδιαφέρει. Τα σημεία που βλέπουμε εφαπτομενικά με την επιφάνεια του νερού, βρίσκονται στο ίδιο υψόμετρο με εμάς.

98. Γιατί ένας καθρέφτης ενώ αντιστρέφει το δεξιά με το αριστερά, δεν αντιστρέφει και το επάνω με το κάτω;

    ΑΠ. Ο επίπεδος καθρέφτης ΔΕΝ αντιστρέφει στην πραγματικότητα ούτε το δεξιά με το αριστερά. Αντανακλά πίσω την εικόνα κάθε περιοχής που καθρεφτίζεται, στην ίδια θέση, επειδή το εστιακό του σημείο βρίσκεται στο άπειρο. Το επάνω καθρεφτίζεται επάνω και το κάτω, κάτω. Το δεξιά καθρεφτίζεται επίσης δεξιά και το αριστερά, αριστερά, αλλά επειδή βλέπουμε τον εαυτό μας κατά πρόσωπο, το δεξιό του ειδώλου είναι το αριστερό μας που έχει αντανακλαστεί προς εμάς και τα αντίστοιχα ισχύουν για την άλλη πλευρά. Αντίθετα, ο φακός της φωτογραφικής μηχανής με το εστιακό του σημείο πριν από το φιλμ (ή τον αισθητήρα) αντιστρέφει όλα τα σημεία, γι' αυτό και η φωτογραφία είναι "σωστή" ως προς το δεξιά-αριστερά, αλλά και ανεστραμμένη (το οποίο φυσικά δεν φαίνεται στην εκτύπωση ή την προβολή της).

99. Είναι γνωστό, ότι υπάρχουν κάποιοι που πιστεύουν ότι η Γη είναι επίπεδη! Ενώ άλλοι, ότι η Γη είναι κούφια (κοίλη Γη) και υπάρχουν όντα, ακόμα και άνθρωποι που ζουν στο εσωτερικό της! Πέρα από τα προφανή επιχειρήματα ενάντια των απόψεων αυτών, ποιο επιχείρημα Φυσικής θα μπορούσε να χρησιμοποιηθεί για δείξει στην τελευταία κατηγορία (τους υποστηρικτές της κοίλης Γης), ότι τα όντα αυτά θα είχαν σοβαρό πρόβλημα να ζήσουν μέσα σε μία κοίλη σφαίρα με ομοιογενή τοιχώματα;

    ΑΠ. Σύμφωνα με το "θεώρημα του κελύφους - shell theorem" που το έχει αποδείξει ο Νεύτωνας, η βαρύτητα στο ελεύθερο εσωτερικό μιας κοίλης σφαίρας είναι μηδέν, σε οποιοδήποτε σημείο της και ανεξάρτητα από το πάχος των τοιχωμάτων (αρκεί να είναι ομοιογενή). Άρα τα όντα αυτά θα έπρεπε να ζουν σε περιβάλλον μηδενικής βαρύτητας, συνεπώς θα απαιτούνταν μεγάλες αλλαγές προσαρμογής σε οποιαδήποτε όντα, πέρα από μικροοργανισμούς.  

100. Στον Διεθνή Διαστημικό Σταθμό, ένας αστροναύτης έχει φέρει μαζί του ένα μπαλόνι (ξεφούσκωτο). Αν το γεμίσει με αέριο ήλιο (που υπάρχει στον Σταθμό), προς τα πού θα κινηθεί το μπαλόνι;

    ΑΠ. Θα μείνει ακίνητο όπου το αφήσει. Μάλιστα το ίδιο θα συμβεί με οτιδήποτε το γεμίσει, ακόμα και με νερό! Το μπαλόνι (με οποιοδήποτε αέριο ή αέρα) θα κινηθεί μόνον εξαιτίας των ρευμάτων αέρα που δημιουργεί στον χώρο ο κλιματισμός (φυσικά όχι αν είναι γεμάτο με νερό, καθώς η αδράνεια εξακολουθεί να υπάρχει). Η άνωση οφείλεται στη διαφορά πίεσης στο κάτω μέρος ενός αντικειμένου, με την πίεση στο επάνω μέρος του, είτε βρίσκεται στον αέρα είτε στο νερό.

101. Σε μία λαμαρίνα διαστάσεων περίπου 30 Χ 30 εκατοστών ανοίγουμε στο κέντρο της μια τρύπα διαμέτρου 10 εκατοστών και θερμάνουμε ομοιόμορφα τη λαμαρίνα. Η διάμετρος της τρύπας θα μεγαλώσει ή θα μικρύνει, αφού η διαστολή γίνεται προς όλες τις κατευθύνσεις?

    ΑΠ. Θα μεγαλώσει. Αυτό είναι εύκολο να το καταλάβουμε αν σχεδιάσουμε την τρύπα στη λαμαρίνα χωρίς να την κόψουμε, και στη συνέχεια θερμάνουμε τη λαμαρίνα. Θα διαπιστώσουμε ότι η διάμετρος του κύκλου έχει μεγαλώσει. Το ίδιο θα είχε συμβεί αν είχαμε κόψει τον κύκλο χωρίς να αφήσουμε κενά, και τον είχαμε αφήσει στη θέση του. Η διαστολή αυξάνει την περίμετρο του κύκλου, άρα και την επιφάνειά του.

102. Ένα ανοικτό βαγονέτο ορυχείου κινείται χωρίς τριβή σε οριζόντιες σιδηροτροχιές σε υπαίθριο χώρο. Ξαφνικά αρχίζει να βρέχει δυνατά. Πώς θα μεταβληθεί η ταχύτητα του βαγονέτου; (Θεωρούμε ότι οι σταγόνες της βροχής που χτυπούν στο εμπρός μέρος του βαγονέτου δεν το επιβραδύνουν και την αντίσταση του αέρα αμελητέα).

    ΑΠ. Θα επιβραδυνθεί, καθώς από το θεώρημα διατήρησης της ορμής ισχύει: m1 x v1 = m2 x v2. Συνεπώς, αφού η μάζα του αυξάνεται καθώς συσσωρεύεται μέσα του νερό, η ταχύτητά του θα μειώνεται. Εναλλακτικά, μπορούμε να σκεφτούμε ότι το νερό που συσσωρεύεται δεν έχει αρχικά οριζόντια ταχύτητα, την οποία θα αποκτήσει δαπανώντας κινητική ενέργεια από το βαγονέτο.

103. Πώς θα μετρήσετε το ύψος ενός κτηρίου μ' ένα χρονόμετρο και ένα βαρόμετρο; (Συχνά, αλλά λανθασμένα, λέγεται ότι το πρόβλημα είχε τεθεί στον Niels Bohr σαν φοιτητή, ο οποίος έδωσε πολλές ευφάνταστες απαντήσεις αποφεύγοντας επίτηδες να δώσει την προφανή, που είναι η παρακάτω).

    ΑΠ. Αν το ύψος του κτηρίου είναι αρκετά μεγάλο, τότε από τη διαφορά της ατμοσφαιρικής πίεσης στη βάση με την κορυφή του, μπορεί να υπολογιστεί το ύψος του. Αν το κτήριο δεν είναι αρκετά ψηλό, η προηγούμενη μέθοδος δεν θα έχει ακρίβεια. Μπορούμε όμως τότε να πετάξουμε το βαρόμετρο από την κορυφή του κτηρίου και να χρονομετρήσουμε την πτώση του, και έτσι να υπολογίσουμε το ύψος του. Αφού το κτήριο δεν θα είναι πολύ ψηλό, η ταχύτητα και ο χρόνος πτώσης δεν θα επηρεαστούν σημαντικά από την αντίσταση του αέρα, οπότε αυτή η μέθοδος θα έχει αρκετή ακρίβεια.

104. Μία γραμματέας σε εταιρεία υψηλής τεχνολογίας διατηρεί ένα ανώνυμο blog που το ενημερώνει κρυφά από τη δουλειά της. Το blog περιέχει διάφορα ανούσια κουτσομπολιά, αλλά περιλαμβάνει και εταιρικά μυστικά που μπορεί να τα διαβάσει μόνο κάποιος συνεργός της απ' έξω. Πώς τα καταφέρνει με έναν απλό τρόπο;

    ΑΠ. Γράφει τις κρυφές φράσεις με γραμματοσειρά που τη "χρωματίζει" στη συνέχεια λευκή, ανάμεσα σε κενά των ορατών προτάσεών της έτσι ώστε τίποτε δεν υποδηλώνει την παρουσία τους. Ο συνεργός της δεν έχει παρά να "φωτίσει" όλο το κείμενο με κάποιο χρώμα εκτός από λευκό, ώστε να εμφανιστεί το κρυμμένο μήνυμα.

105. Ένα σύστημα συναγερμού που ενεργοποιείται /απενεργοποιείται με 4-ψήφιο κωδικό παρουσιάζει πρόβλημα καθώς δεν παίρνει πάντοτε αξιόπιστα τον κωδικό του. Ποια θα ήταν μια απλή λύση;

    ΑΠ. Συνήθως το πρόβλημα προέρχεται από τη φθορά των επαφών των πλήκτρων, όταν χρησιμοποιούνται επανειλημμένα. Η απλή λύση είναι να αλλάξει ο κωδικός με άλλον, που θα χρησιμοποιεί διαφορετικά νούμερα.

106. Μπορεί ένα σκάφος βάρους 100 τόνων να  επιπλεύσει σε νερό βάρους ενός τόνου;

    ΑΠ. Ναι, αν τοποθετηθεί σε μία δεξαμενή λίγο μεγαλύτερη από το κύτος του, η οποία θα γεμίσει με νερό μέχρι το σκάφος να επιπλεύσει. Το σημαντικό είναι να δημιουργηθεί ένα στρώμα νερού (πάχους τουλάχιστον μερικών εκατοστών) μεταξύ κάθε σημείου του κύτους και της δεξαμενής.

107. Ποιο νομίζετε ότι θα ήταν περίπου το μήκος ενός εκκρεμούς που θα είχε ημιπερίοδο (μονή ταλάντωση) 1 δευτερόλεπτο;

    ΑΠ. Περίπου 1 μέτρο (994 εκ), στην επιφάνεια της θάλασσας και σε γεωγραφικό πλάτος 45 μοιρών. Και δεν πρόκειται για σύμπτωση, καθώς εναλλακτικά είχε προταθεί και αυτή η μέθοδος για τον καθορισμό του μέτρου, χωρίς την ανάγκη μετρήσεων ακριβείας σε μεγάλη απόσταση επάνω στη Γη.

108. Μπορεί ο πάγος να βάλει φωτιά;

    ΑΠ. Ναι, με δύο τρόπους. Ο πρώτος είναι να διαμορφωθεί ένα κομμάτι πάγου σε φακό, και να εστιάσει το φως του ήλιου ή άλλης δυνατής φωτεινής πηγής σε εύφλεκτα υλικά. Ο δεύτερος είναι, εάν ένας μεγάλος μετεωρίτης από πάγο μπει στην ατμόσφαιρα της Γης. Στην περίπτωση αυτή, η συμπίεση του αέρα εμπρός από τον μετεωρίτη δημιουργεί υπέρθερμο πλάσμα αέρα (o πάγος δεν θα προλάβει να λιώσει) που θα βάλει φωτιά σε ότι πλησιάσει, ή όπου πέσει.

109. Σ' έναν τελείως σφαιρικό, ομοιογενή και χωρίς ατμόσφαιρα πλανήτη, ανοίγουμε μια διαμπερή τρύπα κατά μήκος μιας διαμέτρου του. Αν ρίξουμε ένα αντικείμενο στην τρύπα από την επιφάνεια του πλανήτη, με τρόπο ώστε να μην ακουμπάει στα τοιχώματα της τρύπας σ' όλη τη διαδρομή του, πως θα κινηθεί το αντικείμενο; Υπάρχει κάτι άλλο που πρέπει να προσέξουμε, εφόσον ο πλανήτης περιστρέφεται;

    ΑΠ. Κατ' αρχήν θα κινηθεί επιταχυνόμενο προς το κέντρο του πλανήτη, αλλά η επιτάχυνση θα μειώνεται συνεχώς, έτσι ώστε να περάσει το κέντρο με μέγιστη ταχύτητα αλλά χωρίς επιτάχυνση. Θα συνεχίσει επιβραδυνόμενο με συμμετρικό τρόπο (ως προς την επιτάχυνση) μέχρι να φτάσει στην επιφάνεια του πλανήτη, στην άλλη άκρη της τρύπας, οπότε θα αντιστρέψει φορά και θα επαναλάβει την ίδια ταλάντωση επ' αόριστο, μια και δεν υπάρχει τριβή με αέρα για να χάσει ενέργεια. Στην ουσία δηλαδή θα κάνει μια ευθύγραμμη ταλάντωση. 

Αν ο πλανήτης είχε το μέγεθος της Γης (πάντα χωρίς ατμόσφαιρα), ο χρόνος για να διασχίσει τον πλανήτη από την μία άκρη στην άλλη θα ήταν 1 ώρα, όσος και ο χρόνος για να κάνει την ίδια απόσταση (δηλαδή τη μισή περίμετρο) σε τροχιά κοντά στην επιφάνεια του πλανήτη.

Εφόσον ο πλανήτης περιστρέφεται, προκειμένου να μην υπάρχουν πλάγιες δυνάμεις (Coriolis) που θα τείνουν να σπρώξουν το αντικείμενο στα τοιχώματα της τρύπας, η τελευταία θα πρέπει να ανοιχτεί κατά μήκος του άξονα περιστροφής του πλανήτη.

110. Υποθέτουμε ότι έχουμε ένα κύκλωμα με μηδενική ωμική αντίσταση από τη Γη στη Σελήνη, που τροφοδοτεί εκεί μια λάμπα με την μπαταρία του κυκλώματος και τον διακόπτη στη Γη. Σε πόσο χρόνο θα ανάψει η λάμπα από τη στιγμή που θα κλείσει ο διακόπτης;

    ΑΠ. Το γρηγορότερο που μπορεί να ανάψει η λάμπα είναι σε 1.5s, καθώς η ταχύτητα μετάδοσης του ηλεκτρισμού είναι ίση με την ταχύτητα του φωτός στο κενό. Όμως ανάλογα με το πόσο κοντά μεταξύ τους είναι οι δύο αγωγοί στη διαδρομή τους από τη Γη στη Σελήνη, η ένταση θα πάρει κάποιο χρόνο να αυξηθεί αρκετά, ώστε η λάμπα να φωτίσει με πλήρη ένταση. Αυτό οφείλεται στην αυτεπαγωγή του κυκλώματος, και ενώ δεν επηρεάζεται από την μηδενική αντίσταση των αγωγών, επηρεάζεται από τη γεωμετρία του κυκλώματος. Όσο πιο κοντά μεταξύ τους οι αγωγοί τόσο μικρότερη η αυτεπαγωγή, το ίδιο και η επιπλέον (μετά το 1.5s) καθυστέρηση.
Ένα ενδιαφέρον σχετικό πείραμα (στα αγγλικά): https://mail.google.com/mail/u/0/?tab=wm#inbox?projector=1

111. Γιατί μία πυρηνική έκρηξη δεν είναι πολύ καταστροφική στο Διάστημα; 

    ΑΠ. Επειδή η καταστροφικότητα μιας πυρηνικής έκρηξης βασίζεται (πέρα από την πολύ έντονη θερμική και ραδιενεργή ακτινοβολία) κυρίως στα κύματα πίεσης του αέρα και στη μετάδοσης θερμότητας με μεταφορά (κυρίως), πάλι μέσω του αέρα, ένας παράγοντας όμως που στο κενό του Διαστήματος λείπει. Γι' αυτό και στις σχετικές ταινίες επιστημονικής φαντασίας, για να καταστραφεί ένας αστεροειδής, η πυρηνική βόμβα πρέπει να θαφτεί βαθιά, οπότε η καταστροφή προκύπτει από την πίεση που αναπτύσσεται από την απότομη εξαέρωση των πετρωμάτων, εξαιτίας της πολύ υψηλής θερμοκρασίας τοπικά.

112. Πώς μπορούμε να χτίσουμε έναν ανθεκτικό τοίχο περίφραξης με μονή σειρά τούβλων:

     ΑΠ. Κάνοντάς τον "κυματιστό", κάτι που συνηθίζεται στη Βρετανία (εικόνα κάτω). Μάλιστα για τοίχο αντίστοιχης αντοχής (και ύψους φυσικά), ο "κυματιστός" χρησιμοποιεί συνολικά λιγότερα τούβλα για το ίδιο μήκος κάλυψης.

113. Ένα μεγάλο πλοίο χρησιμοποιεί μια βαριά άγκυρα με χοντρή αλυσίδα. Αν η άγκυρα σκαλώσει στον βραχώδη πυθμένα και το σκάφος βρεθεί από πάνω της τραβώντας δυνατά με τον μηχανικό "εργάτη" του, σε πιο σημείο κινδυνεύει να σπάσει η αλυσίδα? 

     ΑΠ. Κοντά στον "εργάτη", επειδή στο σημείο εκείνο στη δύναμη που εφαρμόζεται στην άγκυρα προστίθεται και το βάρος της αλυσίδας. Επειδή όμως κάτι τέτοιο θα ήταν επικίνδυνο για το πλήρωμα αλλά θα οδηγούσε και στην απώλεια της αλυσίδας, ο σύνδεσμος (ή κλειδί) που συνδέει την αλυσίδα με την άγκυρα είναι πιο ασθενικός, ώστε να χαθεί μόνον η άγκυρα.

114. Αν στο παρακάτω παιχνίδι, απαντήσετε στην τύχη, ποια είναι η πιθανότητα η απάντηση να είναι η σωστή;

                         

     ΑΠ. Σωστή δεν μπορεί να είναι η επιλογή του 25% γιατί τότε η πιθανότητα θα είναι 50%. Αν πάλι επιλεγεί το 50%, η πιθανότητα είναι 25%. Αν τέλος επιλεγεί το 0%, πάλι η πιθανότητα θα είναι 25%. Άρα δεν υπάρχει σωστή απάντηση.

115. Γνωρίζουμε ότι η κατακόρυφος είναι η συντομότερη τροχιά για να φθάσει μια σφαίρα που αφήνουμε από δεδομένο ύψος στο έδαφος. Αν όμως δεν θέλουμε να φθάσει στο έδαφος από κάτω αλλά σε κάποια απόσταση, πιο σχήμα ράμπας θα μειώσει τον χρόνο στο ελάχιστο.

    ΑΠ. Δεν είναι η ευθεία ράμπα, αλλά μια καμπύλη (Cycloid) που επιτρέπει μια πιο κατακόρυφη κίνηση αρχικά για την ανάπτυξη ταχύτητας αλλά χωρίς μεγάλη "κοιλιά" που θα πρόσθετε χρόνο μετακίνησης. Δεν είναι απλό πρόβλημα, οπότε παρακάτω προσφέρεται μια παραστατική εξήγηση. Έχει όμως ενδιαφέρον, ότι η ευθεία ράμπα είναι (με διαφορά) η πιο αργή διαδρομή.

Και ένα σχετικό βίντεο: https://www.youtube.com/shorts/4Y2Q2H1edeg

116. Δεδομένου ότι ο ήχος ενός κινητήρα jet σε μικρή απόσταση "ακούγεται" με ένταση 150db, ποια φαντάζεστε ότι είναι η μεγαλύτερη (απαραμόρφωτη) ένταση ήχου που μπορεί να μεταδοθεί στη Γη;

    ΑΠ. Λιγότερη από 200db (για την ακρίβεια 194db), καθώς αντιστοιχεί στη μέγιστη διαφορά πίεσης που μπορεί να διατηρηθεί και να μεταδοθεί σε χαμηλό υψόμετρο και 0C. (Προϋποθέτει επίσης ότι δεν προστίθενται αέρια στον αέρα, από μια έκρηξη πχ).

117. Έξω στη φύση, μία λευκή αρκούδα βλέπει έναν πιγκουίνο και αρχίζει να τον καταδιώκει. Η αρκούδα κινείται με 10m/s και ο πιγκουίνος με 2m/s, αλλά προηγείται κατά 80m. Σε πόσο χρόνο θα τον φτάσει η αρκούδα;

    ΑΠ. Η μαθηματική λύση είναι 10s, αλλά το πρόβλημα είναι άκυρο καθώς λευκές αρκούδες και πιγκουίνοι δεν ζουν στο ίδιο ημισφαίριο! (Μπορεί να συμβεί μόνο σε ζωολογικό κήπο!)

118. Βρισκόμαστε επάνω σε μία γέφυρα, η οποία έχει από κάτω ομαλό έδαφος. Έχουμε δύο ίδιες αλυσίδες, με το μήκος της κάθε μιας ίσο με το ύψος του παραπέτου της γέφυρας από το έδαφος. Δένουμε την πρώτη αλυσίδα από το ένα άκρο της στο παραπέτο κοντά μας, και το άλλο της άκρο το κρατάμε, έτσι ώστε η αλυσίδα να κρέμεται διπλή στο κενό μέχρι τη μέση προφανώς της απόστασης από το έδαφος. Τη δεύτερη αλυσίδα την κρατάμε από το ένα άκρο της, αλλά την αφήνουμε να κρεμαστεί στο κενό μέχρι η άλλη άκρη της να αγγίξει το έδαφος. Αφήνουμε ταυτόχρονα τα άκρα των δύο αλυσίδων που κρατάμε, να πέσουν. Ποιας αλυσίδα το άκρο που κρατούσαμε θα φτάσει πρώτο στο έδαφος;

    ΑΠ. Της πρώτης αλυσίδας, επειδή κάθε κρίκος της φτάνοντας στο κάτω σημείο της κοιλιάς (η οποία φυσικά μετατοπίζεται καθώς η αλυσίδα πέφτει) φρενάρει στο ένα άκρο του, οπότε έχει την τάση να περιστραφεί γύρω από το κέντρο βάρος του "τραβώντας" ουσιαστικά με το άλλο άκρο του προς τα κάτω, το τμήμα της αλυσίδας που εξακολουθεί να πέφτει. Το παρακάτω σχήμα εξηγεί τη δυναμική αυτή, προσομοιάζοντας την κίνηση του κρίκου με μία ράβδο που το ένα της άκρο συναντά πρώτο το έδαφος. Το ενδιαφέρον είναι ότι με αυτόν το τρόπο οι τελευταίοι κρίκοι της πρώτης αλυσίδας πέφτουν με ταχύτητα μεγαλύτερη απ' αυτήν που αντιστοιχεί στη γήινη επιτάχυνση!

119. Είναι γνωστό ότι το βάρος μας κοντά στον ισημερινό μειώνεται, τόσο εξαιτίας του σχήματος της Γης που είναι κάπως πεπλατυσμένο (αν και η διαφορά των διαμέτρων είναι μόλις 40km και δεν φαίνεται από το Διάστημα), και της περιστροφής της Γης που τείνει (ελάχιστα βέβαια) να απομακρύνει τα αντικείμενα από την επιφάνειά της. Πόση όμως νομίζετε ότι είναι η μείωση του βάρους από τους πόλους στον ισημερινό, ποσοστιαία;

    ΑΠ. Περίπου 0.5%, δηλαδή ένα αντικείμενο που στους πόλους θα ζύγιζε 100kg (1000N το σωστότερο), στον ισημερινό θα ζύγιζε 99.5kg (995Ν). H μείωση αυτή προέρχεται κυρίως από την απομάκρυνση κατά 20km από το κέντρο της Γης, και πολύ λιγότερο από την περιστροφή της.

120. Έχουμε δύο λάμπες, μία μικρότερης ισχύος και μία μεγαλύτερης, αλλά ίδιας ονομαστικής τάσης 220V. Τις συνδέουμε σε σειρά σε μία πηγή τάσης 440V. Ποια λάμπα κινδυνεύει να καεί;

    ΑΠ. Αυτή της μικρότερης ισχύος, επειδή έχει τη μεγαλύτερη αντίσταση. Αφού από τις δύο σε σειρά λάμπες θα περνάει αναγκαστικά η ίδια ένταση, θα δημιουργείται μεγαλύτερη πτώση τάσης στη λάμπα με την μεγαλύτερη αντίσταση, δηλαδή της μικρότερης ισχύος. Αυτό όμως σημαίνει ότι η λάμπα αυτή θα παίρνει περισσότερη από τη μισή τάση των 440V, δηλαδή πάνω από τα 220V που είναι η ονομαστική της. Άρα είναι η μικρότερη σε ισχύ λάμπα που κινδυνεύει να καεί.

121. Έχουμε 4 αντιστάσεις, κάθε μία τιμής R. Μπορούμε, χρησιμοποιώντας τες όλες να πετύχουμε τιμή R;

    ΑΠ. Θα τις συνδέσουμε ανά δύο σε σειρά, και μετά θα συνδέσουμε τα δύο σετ παράλληλα.

122. Στην παρακάτω εικόνα, αν τραβήξουμε την ελεύθερη άκρη του σχοινιού μέχρι να υπάρχει κάποιο αποτέλεσμα, πόση δύναμη F θα χρειαστεί, και ποιο θα είναι αυτό το αποτέλεσμα;

    ΑΠ. Το βάρος Β της πλάκας μοιράζεται στα δύο άκρα της. Στο δεξιό άκρο, το μισό αυτό βάρος μοιράζεται με τη σειρά του μεταξύ των δύο κάθετων σχοινιών της τροχαλίας, ενώ οι σταθερές τροχαλίες απλά αλλάζουν την κατεύθυνση των δυνάμεων. Άρα όταν η δύναμη F θα είναι η μισή του μισού βάρους Β, δηλαδή Β/4, η πλάκα θα αρχίσει να ανασηκώνεται από τη δεξιά πλευρά. Στην αριστερή πλευρά της πλάκας μεταφέρεται επίσης δύναμη ανύψωσης Β/4, συνεπώς η πλευρά αυτή δεν θα έχει την τάση να μετακινηθεί.

123. Σε μία φάρμα, ένα τρακτέρ είναι παρκαρισμένο σε σημείο που τα πίσω του λάστιχα είναι αρκετά βαθιά μέσα στη λάσπη. Το βράδυ πέφτει ισχυρός παγετός και το πρωί όλα είναι παγωμένα. Ο αγρότης θέλει να χρησιμοποιήσει το τρακτέρ, αλλά ενώ δεν υπάρχει κάποιο εμπόδιο, κάνει πρώτα λίγο πίσω, πριν κινηθεί προς τα εμπρός. Γιατί;

    ΑΠ. Ο αγρότης είναι σωστά ενημερωμένος και φοβάται ότι οι πίσω τροχοί θα έχουν παγιδευτεί στο παγωμένο έδαφος. Στην περίπτωση αυτή, δεδομένης της μεγάλης διαμέτρου των τροχών και της ισχυρής ροπής του κινητήρα, μπορεί το τρακτέρ να "σουζάρει" και να ανατραπεί ταχύτατα από την αντίδραση της ροπής του κινητήρα. Ένας λόγος που τα τρακτέρ έχουν τροχούς μεγάλης διαμέτρου είναι, πέρα από το ότι βουλιάζουν λιγότερο στο μαλακό έδαφος, ότι οι δυνάμεις από το άροτρο "περνούν" κάτω από τον άξονα των πίσω τροχών και πιέζουν το εμπρός μέρος του τρακτέρ προς το έδαφος, παρά τείνουν να το ανυψώσουν.

124. Από ένα ελικόπτερο που πετάει με αρκετή ταχύτητα κρέμεται ένα εύκαμπτο χοντρό σχοινί. Προφανώς η αντίσταση του αέρα θα κάνει το σχοινί να έχει γενικά κλίση προς τα πίσω, ποιό είναι όμως ακριβώς το σχήμα που θα πάρει το σχοινί;

    ΑΠ. Το σχοινί θα είναι σε ευθεία (B), ανεξάρτητα από την ταχύτητα του ελικοπτέρου από την οποία εξαρτάται μόνο η γωνία του. Μάλιστα, κάποιος έκανε πραγματική δοκιμή νοικιάζοντας ελικόπτερο, και έτσι διαπίστωσε επιπλέον ότι το σχήμα του σχοινιού αποκλίνει από την ευθεία, ανάλογα αν στην άκρη του κρεμαστεί αντικείμενο στο οποίο υπερισχύει το βάρος (D) ή αεροδυναμική του αντίσταση (C).
Αυτό γίνεται επειδή αν θεωρήσουμε το σχοινί μοιρασμένο σε ίσα τμήματα, το βάρος και η αντίσταση του αέρα σε κάθε τμήμα του σχοινιού ισορροπούν για την ίδια γωνία σε σχέση με το ελικόπτερο. Αν στο τελευταίο τμήμα του σχοινιού υπερισχύει το βάρος, η θέση ισσορροπίας στο τμήμα αυτό θα είναι πιο κάθετη (για παράδειγμα, όλο το σχοινί θα είχε μια πιο κάθετη θέση αν ήταν βαρύτερο), ενώ το αντίθετο θα συμβεί αν υπερισχύει η αεροδυναμική αντίσταση.

125.

Γιατί ο αριστερά εξωγήινος λέει: "Ας μην απαγάγουμε αυτόν τον τύπο. Μοιάζει με βρυκόλακα."
Και ο δεξιά απαντάει: "Ποιόν τύπο;"

    ΑΠ. Πρόκειται για ανέκδοτο μεταξύ αστρονόμων, που βασίζεται στη δοξασία ότι ένας βρυκόλακας δεν σχηματίζει είδωλο σε καθρέφτη, σε συνδυασμό με το ότι ο αριστερά εξωγήινος χρησιμοποιεί κλασικό διαθλαστικό τηλεσκόπιο (μόνο με φακούς), ενώ ο δεξιά κατοπτρικό τηλεσκόπιο, που περιλαμβάνει και κοίλο κάτοπτρο (καθρέφτη).

126. Είναι γνωστό σε όσους αρέσουν τα κόμικς, ότι ο Λούκυ Λουκ πυροβολεί πιο γρήγορα από τη σκιά του.

Μπορεί όμως ένα πολεμικό αεροσκάφος να καταρρίψει τον εαυτό του με το πυροβόλο του;

    ΑΠ. Αυτό έχει (σχεδόν) συμβεί τον Σεπτέμβριο του 1956, όταν ένα καταδιωκτικό αεροσκάφος F11 Tiger δοκίμασε τα πυροβόλα του πετώντας ανοιχτά της Νέας Υόρκης. Ο πιλότος ξεκίνησε μια ελαφρά υπερηχητική κάθοδο από τα 20.000 πόδια και έριξε δύο σύντομες ριπές πριν συνεχίσει την κάθοδό του, αυξάνοντας μάλιστα τη γωνία της. Έντεκα δευτερόλεπτα αργότερα και ενώ περνούσε από τα 7000 πόδια, κάτι χτύπησε την καλύπτρα και τον κινητήρα του, υποχρεώνοντάς τον σε αναγκαστική προσγείωση από την οποία επέζησε αν και τραυματισμένος. Τρία βλήματα είχαν χτυπήσει το αεροσκάφος όταν πέρασε ανάμεσά τους, καθώς τα βλήματα (παρά την αρχική υπερδιπλάσια ταχύτητά τους) επιβράδυναν σημαντικά από την αντίσταση του αέρα, ενώ το αεροσκάφος συνέχιζε με αμείωτη ταχύτητα και αυξανόμενη γωνία καθόδου.

127. Πόση περίπου ποσότητα νερού διαλυμένη στον αέρα νομίζετε ότι υπάρχει σε ένα κανονικό δωμάτιο, όγκου περίπου 50 κυβικών μέτρων;

    ΑΠ. Ανάλογα με το ποσοστό της σχετικής υγρασία, μεταξύ μισού και ενός κιλού.

128. Γιατί συχνά αυτοί που προκαλούν δυστυχήματα αυτοκινήτου μεθυσμένοι, υφίστανται και τους μικρότερους τραυματισμούς (εφόσον χρησιμοποιούν τη ζώνη ασφαλείας), ειδικά στα άκρα;

    ΑΠ. Γιατί παραμένουν χαλαροί και δεν "τεντώνονται" προκειμένου να στηριχτούν κάπου, βλέποντας το ατύχημα "να έρχεται".

129. Τρείς όμοιες αντιστάσεις (1, 2, 3) είναι συνδεσμολογημένες όπως στο σχήμα. Ποια είναι η ισοδύναμη αντίστασή τους;

  

    ΑΠ. Αυτή που προκύπτει από το παρακάτω απλοποιημένο σχήμα, δηλαδή η ισοδύναμη αντίσταση είναι το 1/3 της τιμής της μιας.

Στο απλοποιημένο σχήμα μπορούμε να καταλήξουμε με τους παρακάτω τρόπους:
α) Βλέποντας ότι το σημείο Α και το Γ είναι ισοδυναμικά, βάζουμε την αντίσταση 1 παράλληλα με την αντίσταση 2. Βλέποντας επίσης ότι το σημείο Β και Δ είναι ισοδυναμικά, βάζουμε την αντίσταση 3 παράλληλα και με την 2, οπότε έχουμε και τις τρείς αντιστάσεις παράλληλες.
β) Το ρεύμα ερχόμενο από το σημείο Α για να φθάσει το Δ μπορεί να ακολουθήσει τη διαδρομή ΑΒΔ, οπότε περνάει μέσα από την αντίσταση 1. Επίσης μπορεί να ακολουθήσει τη διαδρομή ΑΓΔ, οπότε περνάει από την αντίσταση 3. Επίσης τη διαδρομή ΑΓΒΔ, οπότε περνάει από την αντίσταση 2. Άρα περνάει ταυτόχρονα και από τις τρεις αντιστάσεις, κάτι που αντιστοιχεί στην παράλληλη σύνδεσή τους.

130. Είναι γνωστό ότι αν κατέβουμε χαμηλότερα από το επίπεδο της θάλασσας, η ατμοσφαιρική πίεση αυξάνεται. Αυτό έχει επιβεβαιωθεί με μετρήσεις σε ορυχεία, όπου πχ σε βάθος 3.9 km η πίεση έχει μετρηθεί στα 1.6 bar, ενώ στα 58 km εκτιμάται στα 1000 bar. Αν υποθέσουμε ότι η Γη είναι μία ομοιογενής σφαίρα σταθερής θερμοκρασίας 15C και υπάρχει ένα πηγάδι μέχρι το κέντρο της, σε ποιο βάθος η ατμοσφαιρική πίεση θα γίνεται μέγιστη;

    ΑΠ. Η ατμοσφαιρική πίεση είναι αποτέλεσμα της έλξης της Γης στα μόρια της ατμόσφαιρας (οξυγόνου και αζώτου).
Εάν η Γη ήταν ομοιογενής, η έλξη της (που αντιπροσωπεύεται από το g) θα άρχιζε να μειώνεται κάτω από την επιφάνειά της, και θα μηδενίζονταν στο κέντρο της. Επειδή όμως η Γη έχει σιδερένιο πυρήνα, το g μένει περίπου σταθερό μέχρι το βάθος των 2500 km, ενώ στη συνέχεια μειώνεται γρήγορα (εικόνα κάτω). Σε κάθε περίπτωση όμως, καθώς το g παραμένει θετικό, η μέγιστη πίεση αναμένεται να βρίσκεται στο κέντρο της Γης.

Ο υπολογισμός της πίεσης σε μεγάλο βάθος είναι δύσκολος, αλλά ο γράφων βρήκε μία μελέτη (https://www.researchgate.net/publication/226444524_On_the_barometric_formula_inside_the_Earth) που υπολογίζει την πίεση του αέρα στο κέντρο της Γης (εφόσον υπήρχε το υποθετικό πηγάδι και με τις προϋποθέσεις της ερώτησης), στα 220.000 bar! Μάλιστα, ο αέρας κάτω από τα 450 km βάθος θα ήταν ήδη στερεός, εξαιτίας της πίεσης που ξεπερνάει τα 25.000 bar.
Τελικά όχι ένα απλό κουίζ, αλλά πολύ ενδιαφέρον!

131. Ένας μεταλλικός δίσκος με μία τρύπα στο κέντρο θερμαίνεται ομοιόμορφα. Η εξωτερική του διάμετρος προφανώς θα μεγαλώσει, τι θα γίνει όμως με τη διάμετρο της τρύπας; (Παραλλαγή αυτής της ερώτησης υπάρχει και στο Νο 101).

    ΑΠ. Και η διάμετρος της τρύπας θα μεγαλώσει, ανεξάρτητα από το μέγεθός της, και η αύξηση της διαμέτρου θα είναι ανάλογη της αρχικής της διαμέτρου. Αυτή είναι η συνηθισμένη μέθοδος, δηλαδή η θέρμανση, ώστε να προσαρμόζονται εύκολα αλλά τελικά σφιχτά, τροχαλίες, γρανάζια και ρουλεμάν σε άξονες.

Ένας εύκολος τρόπος να το καταλάβουμε είναι να θεωρήσουμε ότι το τμήμα που λείπει είναι στη θέση του. Τότε η διαστολή θα αφορούσε προφανώς και αυτό το τμήμα (επάνω), οπότε δεν έχουμε παρά να σκεφτούμε ότι το αφαιρούμε μετά (κάτω). Μάλιστα η τρύπα διατηρείται κυκλική και μετά τη θέρμανση, ανεξάρτητα από τη θέση της επάνω στον δίσκο.

132. Ένα ποδήλατο είναι στηριγμένο έτσι ώστε να στέκεται όρθιο χωρίς αντίσταση στην κίνησή του εμπρός-πίσω, και χωρίς ολίσθηση του πίσω τροχού ως προς το έδαφος.
Αν δέσουμε ένα σχοινάκι στο πεντάλ του στην κάτω θέση (όπως στην εικόνα) και το τραβήξουμε προς τα πίσω, προς τα πού θα κινηθεί το ποδήλατο;

 

    ΑΠ. Εξαρτάται από τον λόγο μετάδοσης πεντάλ/τροχού. Σε ένα ποδήλατο χωρίς ταχύτητες, το ποδήλατο θα κινηθεί προς τα πίσω παρόλο που το πεντάλ θα τραβήξει το σχοινάκι προς τα εμπρός. Αυτό θα το καταλάβουμε πιο εύκολα αν σκεφτούμε το σχοινάκι δεμένο κοντά στον κεντρικό άξονα του πεντάλ. Αν όμως το ποδήλατο έχει ταχύτητες και χρησιμοποιήσουμε την πρώτη ταχύτητα, τότε το πεντάλ θα τραβηχτεί προς τα πίσω οπότε το ποδήλατο θα κινηθεί (λίγο) προς τα εμπρός. Το κριτήριο είναι αν το μήκος της ευθύγραμμης κίνησης του σχοινιού (στο κάτω μέρος του τόξου που διαγράφει) είναι μικρότερο ή μεγαλύτερο από το μήκος του ίχνους της κίνησης του τροχού.

133. Αυτό μοιάζει σαν το αντίστροφο του προβλήματος Νο 64. Έχει παρατηρηθεί, ότι αν το νερό ενός ποταμού αρχίσει να παγώνει, θα παγώσει τελευταίο στις περιοχές που βρίσκονται κάτω από γέφυρες. Γιατί;

    ΑΠ. Επειδή το πάγωμα του νερού εκλύει θερμότητα (όπως και η συμπύκνωση του ατμού σε νερό). Η γέφυρά παγιδεύει κατά κάποιο τρόπο αυτή τη θερμότητα (ειδικά αν δεν φυσάει) και την αντανακλά προς το νερό από κάτω της, καθυστερώντας το πάγωμά του.

134. Αν πάρουμε μία αλουμινένια κατσαρόλα, τη γεμίσουμε μέχρι επάνω με νερό βρύσης και τη θερμάνουμε ομοιόμορφα ώστε η θερμοκρασία της να ανέβει (μαζί με το νερό) κατά 10 βαθμούς Κελσίου, το νερό θα ξεχειλίσει ή θα κατέβει η στάθμη του μέσα στην κατσαρόλα;

    ΑΠ. Θα ξεχειλίσει, επειδή ο συντελεστή διαστολής του νερού είναι τριπλάσιος του συντελεστή διαστολής όγκου του αλουμινίου. Γενικά οι συντελεστές διαστολής των υγρών είναι πολύ μεγαλύτεροι των στερεών και βέβαια ο επιπλέον όγκος των στερεών εξαιτίας θερμικής διαστολής δεν αλλάζει, είτε είναι συμπαγή είτε "κούφια".

135. Είναι γνωστό ότι η Αυστραλία είναι "ανάποδα" σε σχέση με τις περισσότερες ηπείρους στη Γη, αλλά φυσικά οι Αυστραλοί δεν το καταλαβαίνουν αυτό, καθώς είναι κυρίως οι διαφορετικοί αστερισμοί που τους θυμίζουν αυτή τη ιδιαιτερότητα. Υπάρχει όμως κάτι που το βλέπουν πραγματικά ανάποδα;

ΑΠ. Τη Σελήνη, την οποία πράγματι βλέπουν ανάποδα και στην οποία καθώς υπάρχουν χαρακτηριστικές "θάλασσες" είναι εύκολο να διαπιστωθεί η διαφορά. Φυσικά και τον Ήλιο βλέπουν ανάποδα, αλλά στην περίπτωση αυτή πρακτικά δεν υπάρχει διαφορά.

136. Αν έχουμε δύο μεταλλικές σφαίρες μάζας 1kg την κάθε μια, σε απόσταση μεταξύ των κέντρων τους 1m, και στηριγμένες χωρίς καθόλου τριβή (πχ με μαγνητική αιώρηση), σε πόσο χρόνο εκτιμάτε ότι θα έρθουν να ακουμπήσουν μεταξύ τους εξαιτίας τηε βαρυτικής τους έλξης;

Όχι το ίδιο, αλλά ένα πείραμα για τη μέτρηση της παγκόσμιας βαρυτικής σταθεράς (πείραμα Caventish). Οι πράσινες σφαίρες είναι σταθερές ενώ οι γαλάζιες αναρτώνται με τρόπο που δίνει σημαντική συστροφή με πολύ μικρή ροπή (πχ με πολύ λεπτό και μακρύ σύρμα.

    ΑΠ. Ένας σχετικά απλός υπολογισμός χρησιμοποιώντας τον νόμο της παγκόσμιας έλξης μεταξύ τους και τον νόμο της επιτάχυνσης (για μεγαλύτερη ακρίβεια θα πρέπει να ληφθεί υπόψη η αύξηση της έλξης και συνεπώς και της επιτάχυνσης καθώς οι σφαίρες πλησιάζουν), δίνει χρόνο περίπου 24 ωρών.

137. Γνωρίζουμε ότι όλα τα συνηθισμένα υλικά διαστέλλονται με την αύξηση της θερμοκρασίας τους. Υπάρχει όμως ένα κοινό υλικό που συστέλλεται με την αύξηση της θερμοκρασίας του. Ποιό είναι αυτό και γιατί;

    ΑΠ. Τα κοινά "λαστιχάκια". Και αυτό, επειδή θα πρέπει να φανταστούμε τα μόριά τους σαν τους μακρόστενους κρίκους μιας αλυσίδα που σε θερμοκρασία δωματίου είναι τεντωμένη στο έδαφος. Με την αύξηση της θερμοκρασίας κάθε κρίκος "ζωηρεύει" και αρχίζει να πάλλεται και να συστρέφεται, έτσι το συνολικό μήκος της αλυσίδας θα γίνει μικρότερο απ' όταν οι κρίκοι ήταν ήρεμοι και τεντωμένοι.

138. Ποιό είναι το αγαπημένο καρτούν των Φυσικών;

    ΑΠ. Το κογιότ (Wile E. Coyote & Road Runner*) επειδή καταστρατηγεί τόσο εμφανώς, αλλά και ευρηματικά τους νόμους της Φυσικής, και κάθε επεισόδιο αποτελεί πρόκληση να εντοπίσεις όλα τα "λάθη Φυσικής" που περιέχει!

Συνιστώμενο βίντεο: https://www.youtube.com/watch?v=Aewj-0wcMIo

* Στα αγγλικά, το καρτούν που υπάρχει αναλλοίωτο σχεδιαστικά από το 1949(!) αναφέρεται συνήθως με το όνομα του πουλιού (Road Runner) που είναι υπαρκτό (Γεωκόκκυγας της Καλιφόρνιας), το οποίο αν και μπορεί να πετάει προτιμάει να ξεφεύγει τρέχοντας από τους θηρευτές του, με ταχύτητα που μπορεί να φτάσει τα 40 χλμ/ω.

139. Υπάρχει περίπτωση κάποιος να "νιώσει" τον εγκέφαλό του;

    ΑΠ. Ναι, αν βρίσκεται σε διαδικασία εγχείρησης στον εγκέφαλό του, που γίνεται με τον ασθενή "ξύπνιο" ώστε ο χειρουργός να ελέγχει συνεχώς την εγκεφαλική λειτουργία. Αν ο ασθενής (φορώντας γάντι) αγγίξει τον εκτεθειμένο εγκέφαλό του, θα τον νοιώσει με το χέρι του (μέσω του εγκεφάλου του φυσικά), ο ίδιος όμως ο εγκέφαλος δεν θα νιώσει τίποτα επειδή δεν έχει αντίστοιχες νευρικές απολήξεις.

140. Ένας μηχανικός βρίσκεται στο βάθος ενός ορυχείου, 100 περίπου μέτρα κάτω από την επιφάνεια του εδάφους. Πρέπει να ανοίξει μία υπόγεια σήραγγα μήκους 10km, απόλυτα οριζόντια σε όλο το μήκος της. Καταβάλει κάθε προσπάθεια ώστε ο άξονας της σήραγγας να είναι οριζόντιος στο σημείο εκκίνησης και χρησιμοποιεί ακτίνα laser για να βεβαιωθεί ότι θα είναι απόλυτα ευθής σ' όλο το μήκος του. Παρόλα αυτά, όταν ελέγχει την άκρη της σήραγγας στο τέλος των 10km βρίσκει ότι αποκλίνει σαφώς από την οριζοντιότητα. Τι μπορεί να πήγε λάθος;

    ΑΠ. Δεν έλαβε υπόψην του την καμπυλότητα της Γης, που στα 10km παρουσίαζει περίπου 8m απόκλιση κατά την κατακόρυφο, κάτι που επιβεβαιώνεται με απλή χρήση του Πυθαγόρειου θεωρήματος.

141. Ο οδηγός ενός ηλεκτρικού αυτοκινήτου προγραμματίζει να κάνει μία διαδρομή που θα είναι αρκετά κατηφορική και με στροφές. Πριν τη διαδρομή σκέφτεται να φορτίσει το αυτοκίνητό του, αλλά όχι στο 100%, ώστε να πετύχει τη μέγιστη απόδοση. Είναι το σκεπτικό του σωστό;  

 

    ΑΠ. Είναι σωστό, γιατί έτσι η μπαταρία του αυτοκινήτου του θα έχει περιθώριο να προσθέσει φόρτιση από το αναγεννητικό φρενάρισμα (που θα είναι συχνό), και να πετύχει χαμηλότερη τιμή κόστους/km.

142. Η παρακάτω εικόνα προέρχεται από ένα παλιό λεξικό που εξηγεί την αγγλική λέξη "parbuckle" και φυσικά πρόκειται για το σύστημα της εικόνας, για την ανύψωση κυλινδρικών αντικειμένων σε κεκλιμένο επίπεδο. 

Το ερώτημα είναι, αν υποθέσουμε ότι το κεκλιμένο επίπεδο έχει κλίση 30 μοιρών ως προς το οριζόντιο, και ότι το βαρέλι ζυγίζει 100kg (1000N), πόση δύναμη πρέπει να βάλει ο άνθρωπος για να το σύρει.

    ΑΠ. Ίσως να θυμάστε από τα κεκλιμένα επίπεδα, ότι για κλίση 30 μοιρών η δύναμη ισορροπίας είναι το μισό του βάρους, δηλαδή στην περίπτωση αυτή 50kg. Η δύναμη που βάζει ο άνθρωπος μέσω του σχοινιού (συνολικά και με τα δύο χέρια) είναι η μισή από τη δύναμη ισορροπίας, επειδή εφαρμόζεται με υπομόχλιο το κάτω μέρος του βαρελιού και όχι το κέντρο του. Άρα η δύναμη που πρέπει να εφαρμόσει ο άνθρωπος είναι 25kg (και σε σωστές μονάδες, 250Ν).

143. Είναι δυνατόν ένα σώμα σε ελεύθερη πτώση (χωρίς οριζόντια ταχύτητα) να πέφτει πιο αργά εφόσον περιστρέφεται με αρκετή ταχύτητα, παρά αν δεν περιστρέφεται;

ΑΠ. Ναι, και υπάρχουν δύο περιπτώσεις. 

1. Η περιστροφή να δημιουργεί εξαιτίας του σχήματός του κάποια άντωση, πχ αν έχει το σχήμα έλικας, ή κάτι παρόμοιο.

2. Η περιστροφή εξαιτίας του γυροσκοπικού φαινομένου να σταθεροποιεί το σώμα, έτσι ώστε να προβάλλει τη μέγιστη αντίσταση στον αέρα, πχ ένας δίσκος που περιστρέφεται με το επίπεδό του παράλληλο προς το έδαφος.

144. Ένας επιβάτης ενός εμπορικού αεροσκάφους, έχει ένα φουσκωτό μαξιλαράκι αυχένα. Το φουσκώνει πριν την απογείωση, αλλά όχι τελείως. Γιατί;

ΑΠ. Επειδή αναμένει ότι όταν το αεροσκάφος θα ανέβει στο ύψος πτήσης (10-12 χιλιόμετρα), η διαφορά πίεσης θα το φουσκώσει τελείως (η πίεση στην καμπίνα του αεροσκάφους αντιστοιχεί στα 2.5 περίπου χιλιόμετρα, για να μειώνεται η καταπόνηση της δομής του από τις επαναλαμβανόμενες αυξομειώσεις πίεσης). Αν ήταν τελείως φουσκωμένο από το έδαφος, θα κινδύνευε να σκιστεί από την πίεση. Αυτό το φαινόμενο παρατηρείται και στα μπουκάλια νερού από μαλακό πλαστικό, που αφού ανοιχτούν και ξανακλείσουν στο ύψος πτήσης, βρίκονται κάπως τσαλακωμένα κατά την προσγείωση.

145. Γιατί ο ηλεκτρικός τροχός με τον οποίο ο ορθοπεδικός κόβει τον γύψο ή το πλαστικό μετά την αποκατάσταση ενός κατάγματος, δεν μπορεί να πληγώσει το δέρμα;

ΑΠ. Επειδή σε αντίθεση με τον τροχό των τεχνιτών, ο δίσκος δεν περιστρέφεται αλλά ταλαντώνεται ελάχιστα χιλιοστά, οπότε αν φτάσει στο δέρμα απλά το μετατοπίζει ελαφρά χωρίς να το κόβει, εξαιτίας της ελαστικότητάς του. Κάτι που φυσικά δεν ισχύει για τα σκληρά υλικά.

146. Αν μία μοτοσυκλέτα έχει το ίδιο μεταξόνιο (απόσταση του εμπρός με τον πίσω τροχό) με ένα αυτοκίνητο και τον εμπρός τροχό της στραμμένο ακριβώς στην ίδια γωνία με αυτούς του αυτοκινήτου, θα έχει και τον ίδιο κύκλο στροφής; 

ΑΠ. Όχι, καθώς η μοτοσυκλέτα για να στρίψει θα πρέπει να γύρει προς τη στροφή, οπότε ο εμπρός τροχός της επιπλέον αποτελεί βάση κώνου (κάτι που δεν συμβαίνει στο αυτοκίνητο), οπότε ο κύκλος στροφής της θα είναι μικρότερος. Μάλιστα βάση κώνου διαγράφει και ο πίσω τροχός.

147. Είστε στην ύπαιθρο και πλησιάζει καταιγίδα, ενώ η ατμόσφαιρα έχει σκοτεινιάσει. Στο βάθος φαίνονται σποραδικά  κεραυνοί, ο ήχος των οποίων ακούγεται μετά από 15 περίπου δευτερόλεπτα. Σε πόση απόσταση περίπου πέφτουν οι κεραυνοί, και τι ώρα είναι;

ΑΠ. Η ταχύτητα του ήχου είναι 340m/s. Άρα κάθε τρία δευτερόλεπτα περίπου ο ήχος διατρέχει ένα χιλιόμετρο. Συνεπώς τα 15 δευτερόλεπτα αντιστοιχούν σε 5 km. Οσο για την ώρα, είναι ώρα για να αναζητήσετε κάλυψη!

148. Στη διάταξη που απεικονίζεται στην ερώτηση 136 (αλλά όχι με τη μεθοδολογία προσδιορισμού της παγκόσμιας βαρυτικής σταθεράς) και υποθέτοντας ότι το πείραμα γίνεται στην Ισλανδία, βλέπετε κάτι που θα έπρεπε να ληφθεί υπόψη για τον προσδιορισμό του χρόνου προσέγγισης μεταξύ των σφαιρών, που σχετίζεται με άλλο διάσημο πείραμα;

ΑΠ. Την (σχετική) περιστροφή του αναρτημένου ζεύγους εξαιτίας της περιστροφής της Γης, όπως έδειξε το πείραμα του Foucault στο Παρίσι το 1851. Στην πραγματικότητα, είναι το αναρτημένο ζεύγος των σφαιρών που δεν περιστρέφεται εξαιτίας της σημαντικής αδράνειάς του, ενώ η Γη μαζί τα σταθερά βάρη γυρίζει σε σχέση με τα πρώτα.

Σημείωση: Το πείραμα για τον προσδιορισμό της παγκόσμιας βαρυτικής σταθεράς, γίνεται με τρόπο ώστε η περιστροφή της Γης δεν το επηρεάζει.

149. Έχουμε πέντε πουγγιά με χρυσές λίρες. Από αυτά, σ' ένα μόνο πουγγί όλες οι λίρες είναι κάλπικες, ενώ στα άλλα τέσσερα όλες είναι γνήσιες. Μία χρυσή λίρα από μία κάλπικη δεν διαφέρουν εξωτερικά, αλλά η κάλπικη ζυγίζει ένα γραμμάριο λιγότερο από τη γνήσια που ζυγίζει 8 γραμμάρια. Μπορούμε με μία μόνο μέτρηση σε ζυγό ακριβείας να βρούμε πιο πουγγί περιέχει τις κάλπικες λίρες;

(Από το βιβλίο του Νίκου Λ. Πασχαλούδη "Τότε Που Παίζαμε").

ΑΠ. Βάζουμε τα πουγγιά στη σειρά, και πέρνουμε από πρώτο πουγγί μία λίρα, από το δεύτερο δύο, κλπ και φυσικά από το πέμπτο πουγγί πέντε λίρες, και τις ζυγίζουμε όλες μαζί. Αν και οι 15 αυτές λίρες ήταν γνήσιες το αποτέλεσμα θα ήταν 120 γραμμάρια. Όσα γραμμάρια λιγότερα θα δείξει η ζύγιση, σε αυτή τη θέση θα βρίσκεται το πουγγί με τις κάλπικες. Αν δείξει για  παράδειγμα 117 γραμμάρια, το πουγγί θα είναι το τρίτο στη σειρά.

150. Έχετε παρατηρήσει ότι όταν πάτε να ξανανοίξετε την πόρτα του ψυγείου, αφού την έχετε κλείσει λίγο πριν, δυσκολεύεστε περισσότερο από το συνηθισμένο? Γιατί?

ΑΠ. Μόλις ανοίξετε την πόρτα του ψυγείου, κρύος αέρας από το εσωτερικό του ρέει προς τα έξω και αντικαθίσταται από θερμότερο του περιβάλλοντος. Όταν κλείσετε πάλι την πόρτα, ο αέρας αυτός ψύχεται γρήγορα και συστέλλεται, με αποτέλεσμα να δημιουργηθεί μικρή υποπίεση. Αν πάτε να την ξανανοίξετε λίγο μετά, η μικρή αυτή υποπίεση σας εμποδίζει περισσότερο από ότι συνήθως* στο άνοιγμα, καθώς η πόρτα έχει μεγάλη επιφάνεια. Μετά από κάποιο διάστημα όμως η πίεση εξισορροπείται, εξαιτίας των αναπόφευκτων διαρροών από το λάστιχο της πόρτας.

*Κάτω από το λάστιχο της πόρτας υπάρχουν μαγνήτες για καλύτερη σφράγιση.

151. Ένα εμπορικό τρένο με ατμομηχανή και πολλά βαγόνια ξεκινάει από τον σταθμό. Αρχικά όμως ο μηχανοδηγός κάνει το τρένο να οπισθοχωρήσει κατά μερικά μέτρα, πριν να σταματήσει και ξεκινήσει κανονικά. Γιατί;

ΑΠ. Αυτό θα μειώσει τα διάκενα που πάντα υπάρχουν στις συνδέσεις μεταξύ των βαγονιών, ώστε το τρένο να μην ξεκινήσει με όλο το φορτίο αλλά αυτό να προστεθεί προοδευτικά, για να μην πατινάρουν οι τροχοί της ατμομηχανής. Αυτό είναι ιδιαίτερα έντονο με τις ατμομηχανές που έχουν μόνον τρεις κινητήριους άξονες και μεταφέρουν μεγάλη ροπή στους τροχούς, οι οποίοι επιπλέον έχουν χαμηλή πρόσφυση καθώς ο συντελεστής τριβής σίδερο με σίδερο είναι σχετικά μικρός.

152. Αν φέρουμε σε επαφή 1g ύλης με 1g αντιύλης, σύμφωνα με τον τύπο E = mc² πόση μάζα θα μετραπεί πλήρως σε ενέργεια;

ΑΠ. Το σύνολο της ύλης και της αντιύλης, δηλαδή 2g. Για σύγκριση, στις "συμβατικές" πυρηνικές ή θερμοπυρηνικές εκρήξεις, δεν μετρέπεται σε ενέργεια πάνω από το 1% της σχάσιμης μάζας.